第 119 章 似然的概念和圖形理解 Likelihood
本章的練習,我們主要使用四個計算似然的命令來加深我們對似然這一概念的理解:
blik: binomial likelihood (二項分佈的似然)plik: Poisson likelihood (泊松分佈的似然)bloglik: binomial log-likelihood (二項分佈的對數似然)ploglik: Poisson log-likelihood (泊松分佈的對數似然)
119.1 Q1 二項分佈似然的圖形
在R語言中繪製二項分佈參數 \(\pi\) 在不同情況下的似然函數圖:
- 10次實驗中4次失敗:
x <- seq(0,1,by=0.001)
y <- (x^4)*((1-x)^6) / (0.4^4*0.6^6)
plot(x, y, type = "l", ylab = "LR(\U03C0)", xlab = "\U03C0")
abline(v=0.4, lty=2)
abline(h=1.0, lty=2)
abline(h=0.1466, lty=2, lwd = 2, col = "red")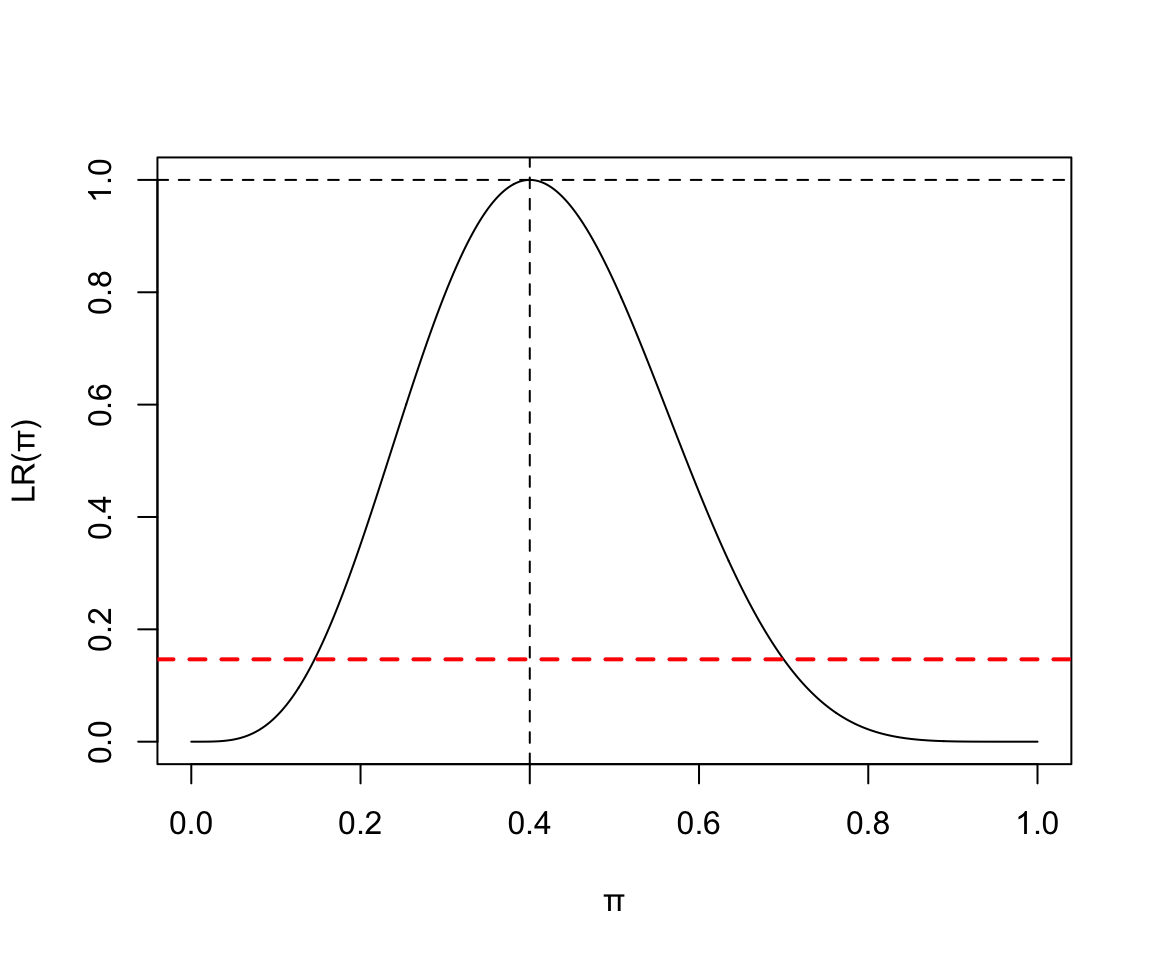
圖 119.1: Binomial(10, 4) Likelihood ratio
2,100次實驗中40次失敗:
x <- seq(0,1,by=0.001)
y <- (x^40)*((1-x)^60) / (0.4^40*0.6^60)
plot(x, y, type = "l", ylab = "LR(\U03C0)", xlab = "\U03C0")
abline(h=1.0, lty=2)
abline(v=0.4, lty=2)
abline(h=0.1466, lty=2, lwd = 2, col = "red")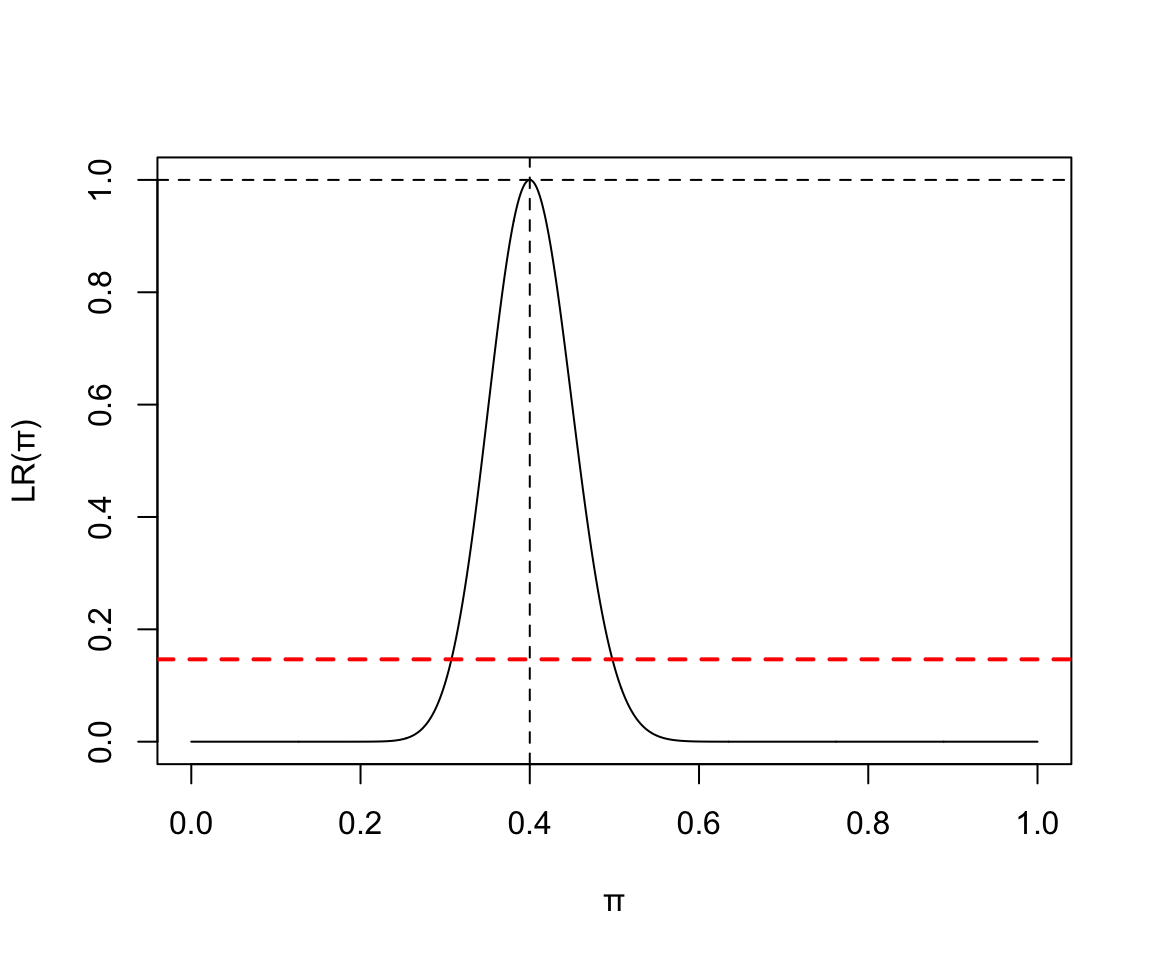
圖 119.2: Binomial(100, 40) Likelihood ratio
- 1000 次實驗中 400 次失敗:
x <- seq(0,1,by=0.001)
y <- (x^400)*((1-x)^600) / (0.4^400*0.6^600)
plot(x, y, type = "l", ylab = "LR(\U03C0)", xlab = "\U03C0")
abline(v=0.4, lty=2)
abline(h=1.0, lty=2)
abline(h=0.1466, lty=2, lwd = 2, col = "red")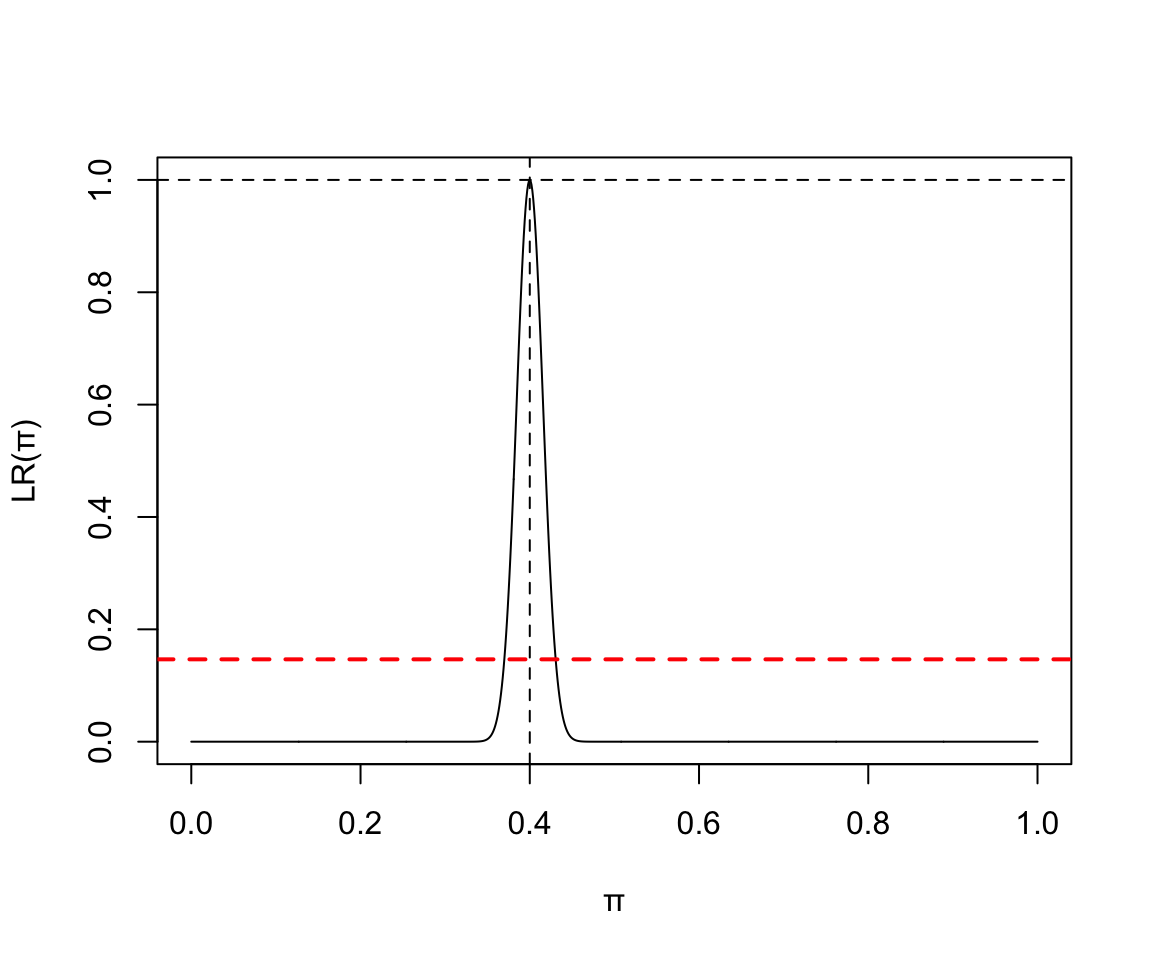
圖 119.3: Binomial(1000, 400) Likelihood ratio
三個圖的整體信息告訴我們,數據越多,對參數的估計越精確 (more data more precise estimate)。
119.2 Q2 修改信賴區間的寬度
把紅線刻度從 0.1466 改成 0.2585,會發生怎樣的改變?
x <- seq(0,1,by=0.001)
y <- (x^40)*((1-x)^60) / (0.4^40*0.6^60)
plot(x, y, type = "l", ylab = "LR(\U03C0)", xlab = "\U03C0")
abline(h=1.0, lty=2)
abline(v=0.4, lty=2)
abline(h=0.2585, lty=2, lwd = 2, col = "red")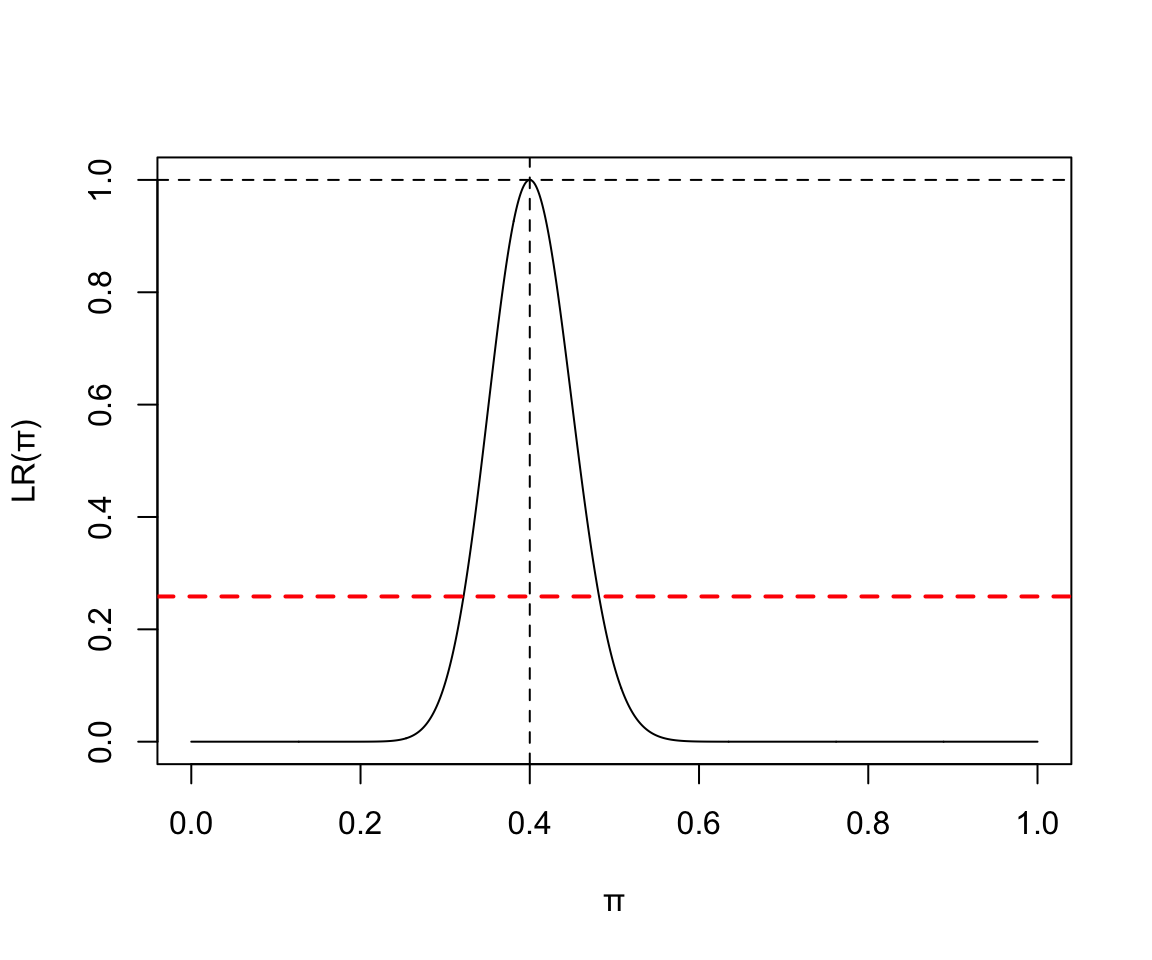
圖 119.4: Binomial(100, 40) Likelihood ratio, with 90% CI.
當改成使用 90% 信賴區間的時候,區間變窄,但其實我們對這個區間的長期重複實驗結果是否包含真實參數值的信心變小了。(less confident about the interval)
119.3 Q3 嘗試繪製一些極端情況下的似然函數圖
- 假如繪製如 10 次實驗中 1 次失敗的二項分佈參數似然函數圖:
x <- seq(0,1,by=0.001)
y <- (x^1)*((1-x)^9) / (0.1^1*0.9^9)
plot(x, y, type = "l", ylab = "LR(\U03C0)", xlab = "\U03C0")
abline(v=0.1, lty=2)
abline(h=1.0, lty=2)
abline(h=0.1466, lty=2, lwd = 2, col = "red")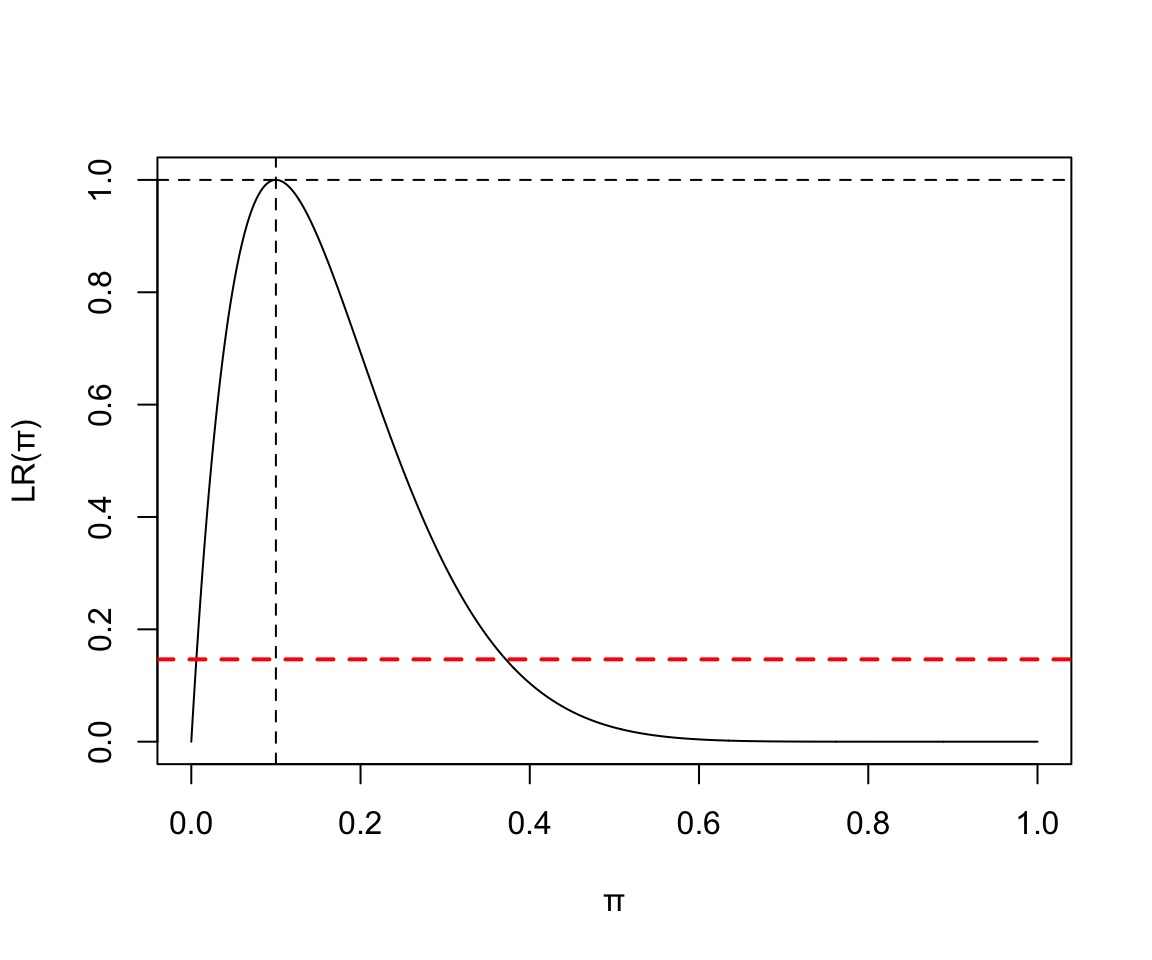
圖 119.5: Binomial(10, 1) Likelihood ratio
- 假如繪製如 100 次實驗中 1 次失敗的二項分佈參數似然函數圖:
x <- seq(0,1,by=0.001)
y <- (x^1)*((1-x)^99) / (0.01^1*0.99^99)
plot(x, y, type = "l", ylab = "LR(\U03C0)", xlab = "\U03C0")
abline(v=0.01, lty=2)
abline(h=1.0, lty=2)
abline(h=0.1466, lty=2, lwd = 2, col = "red")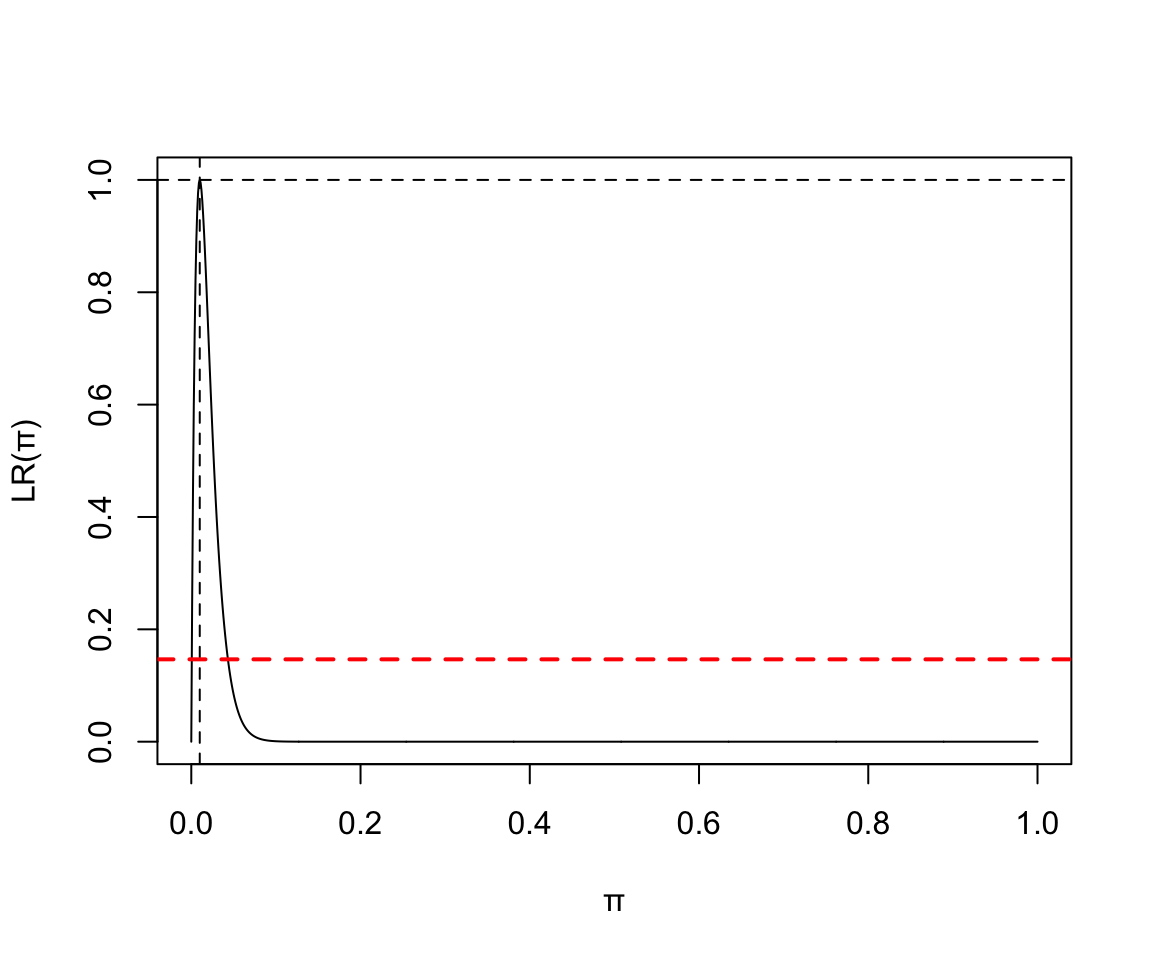
圖 119.6: Binomial(100, 1) Likelihood ratio
當實驗結果或數據較爲極端的時候,我們發現似然比不再和正(常)態分佈近似,也越來越偏向一邊。(no longer symmertrical and bell-shaped with extreme splits)
119.4 Q4 失敗次數爲 0 會發生什麼
當多次實驗中觀察到 0 次失敗,那麼似然函數會變成怎樣?
- 10次實驗中0次失敗:
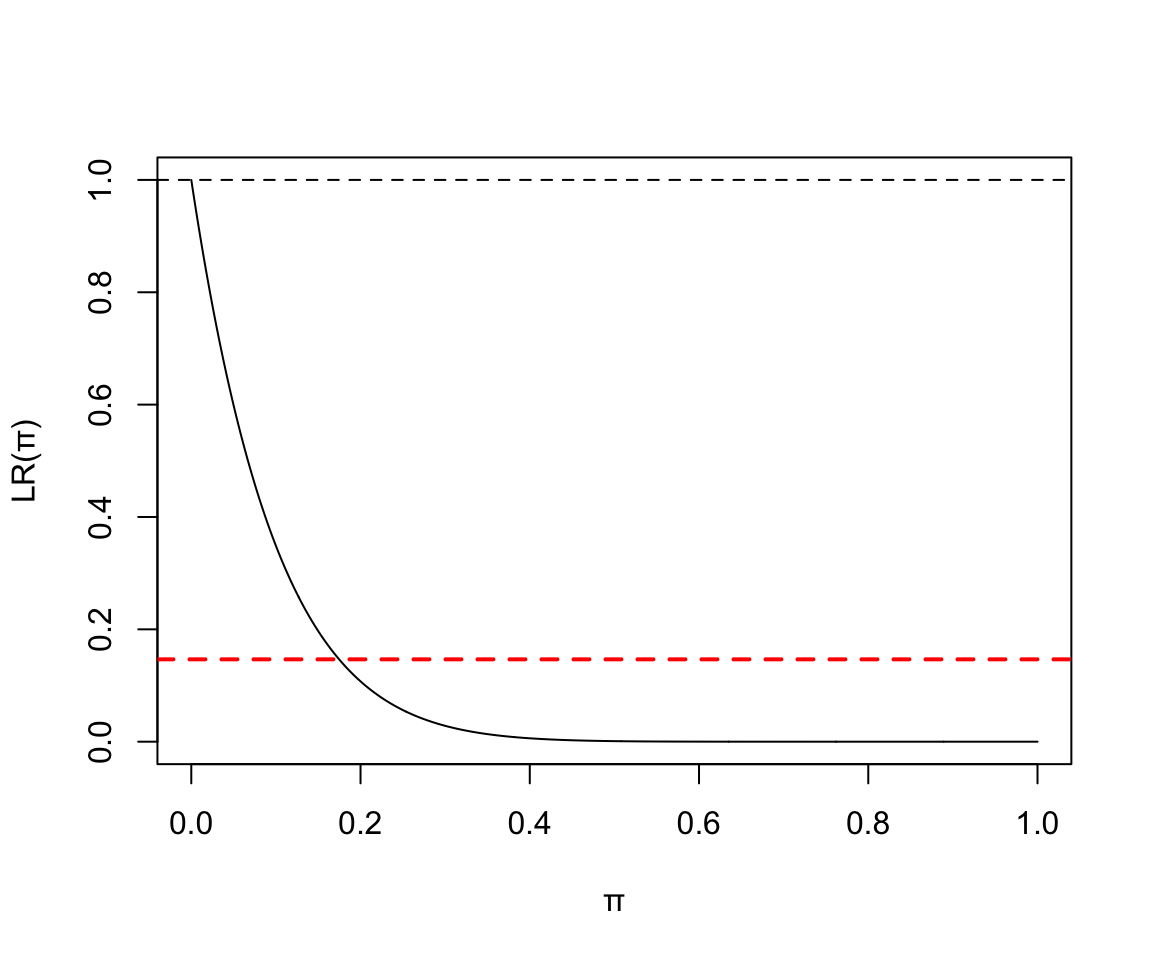
圖 119.7: Binomial(10, 4) Likelihood ratio
2,100次實驗中0次失敗:
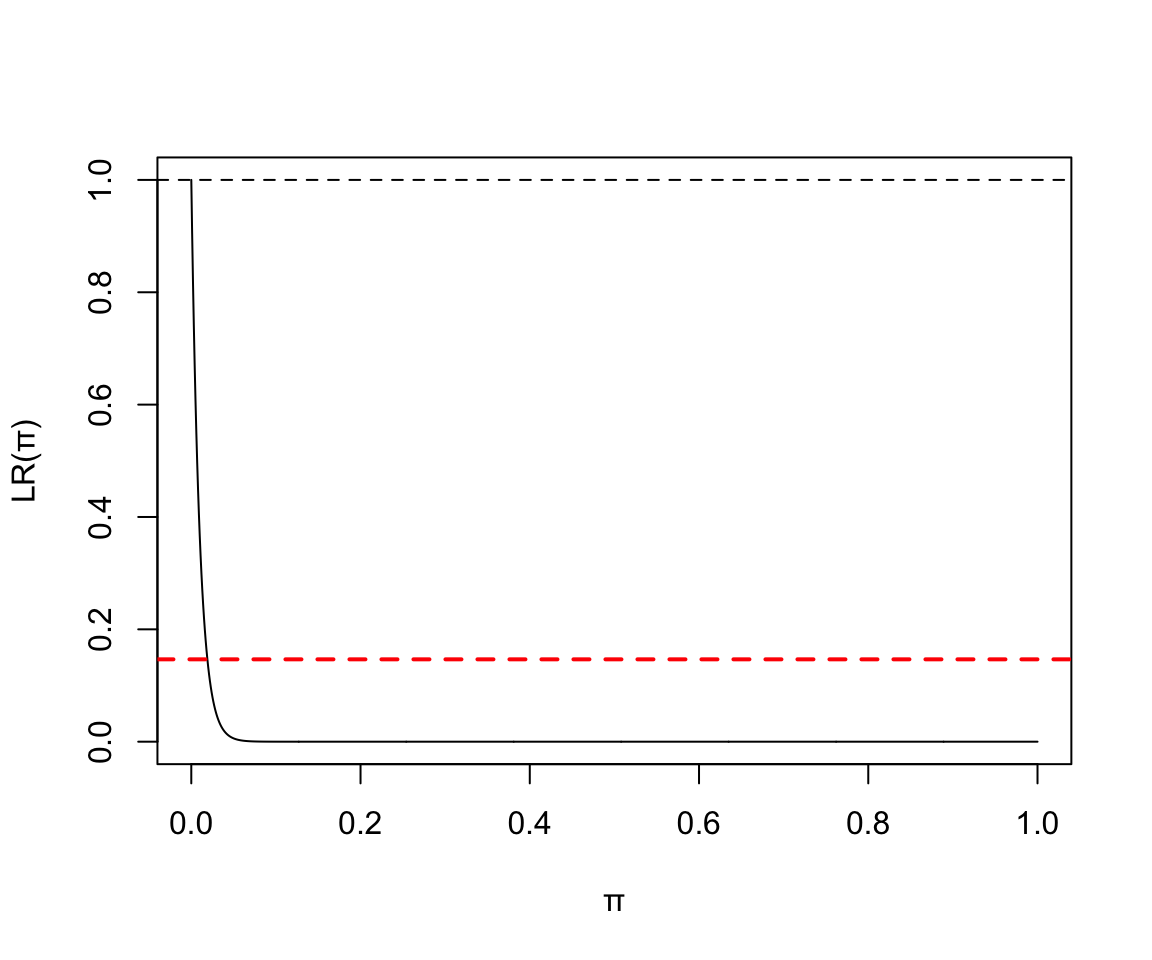
圖 119.8: Binomial(100, 40) Likelihood ratio
- 1000 次實驗中 0 次失敗:
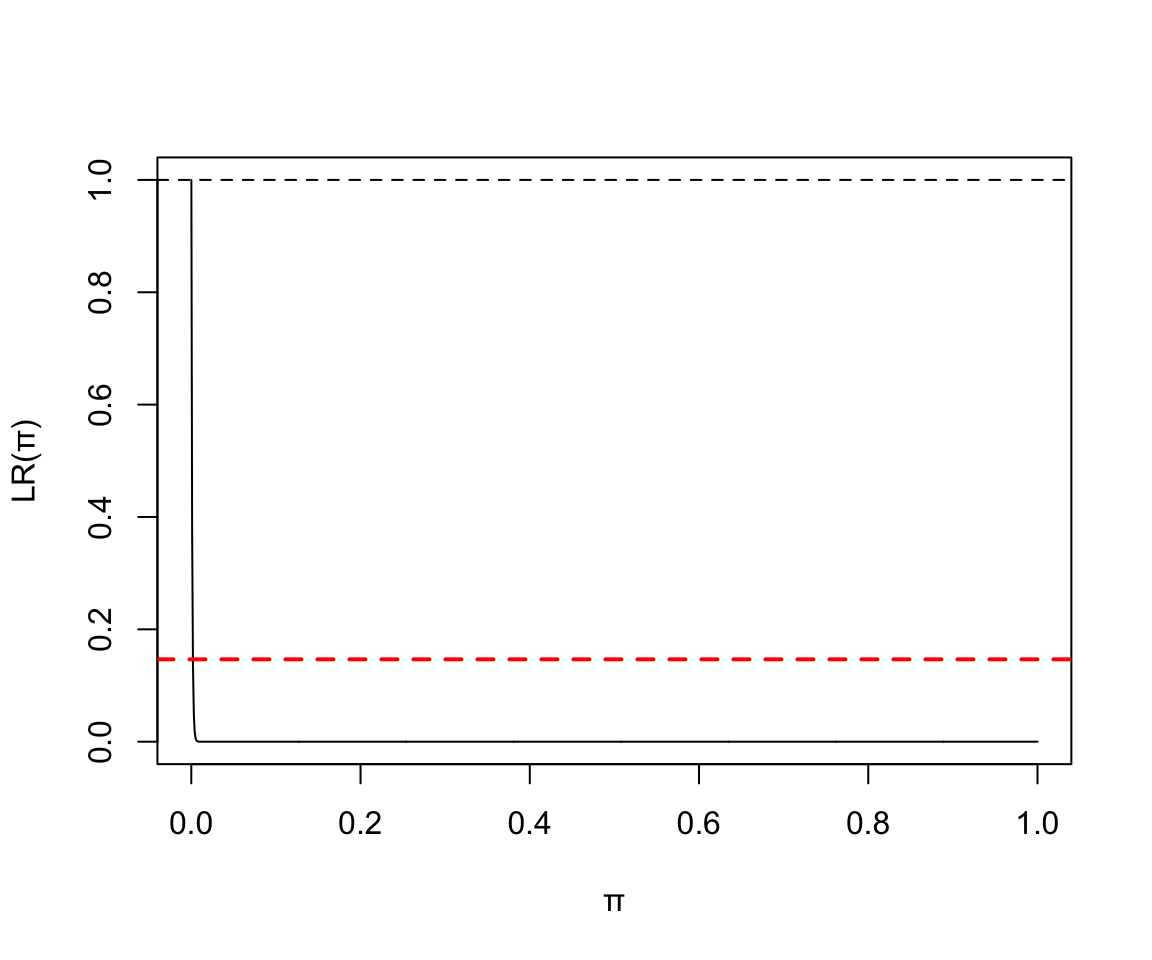
圖 119.9: Binomial(1000, 400) Likelihood ratio
於是我們知道當沒有失敗時,二項分佈數據的參數 \(\pi\) 的似然函數沒有轉折點。(no turning point)
119.5 Q5 泊松分佈參數的似然函數
在R語言中繪製泊松分佈參數 \(\lambda\) 在不同情況下的似然函數圖:
- 500人年的觀察中發現7人死亡:
x <- seq(0, 40, by=0.1)/1000
y <- exp( -500 * x + 7 + 7 * log( x * 500) - 7 * log(7))
plot(x, y, type = "l", ylab = "LR(\u03BB)", xlab = ~lambda)
abline(h=1.0, lty=2)
abline(h=0.1466, lty=2, lwd = 2, col = "red")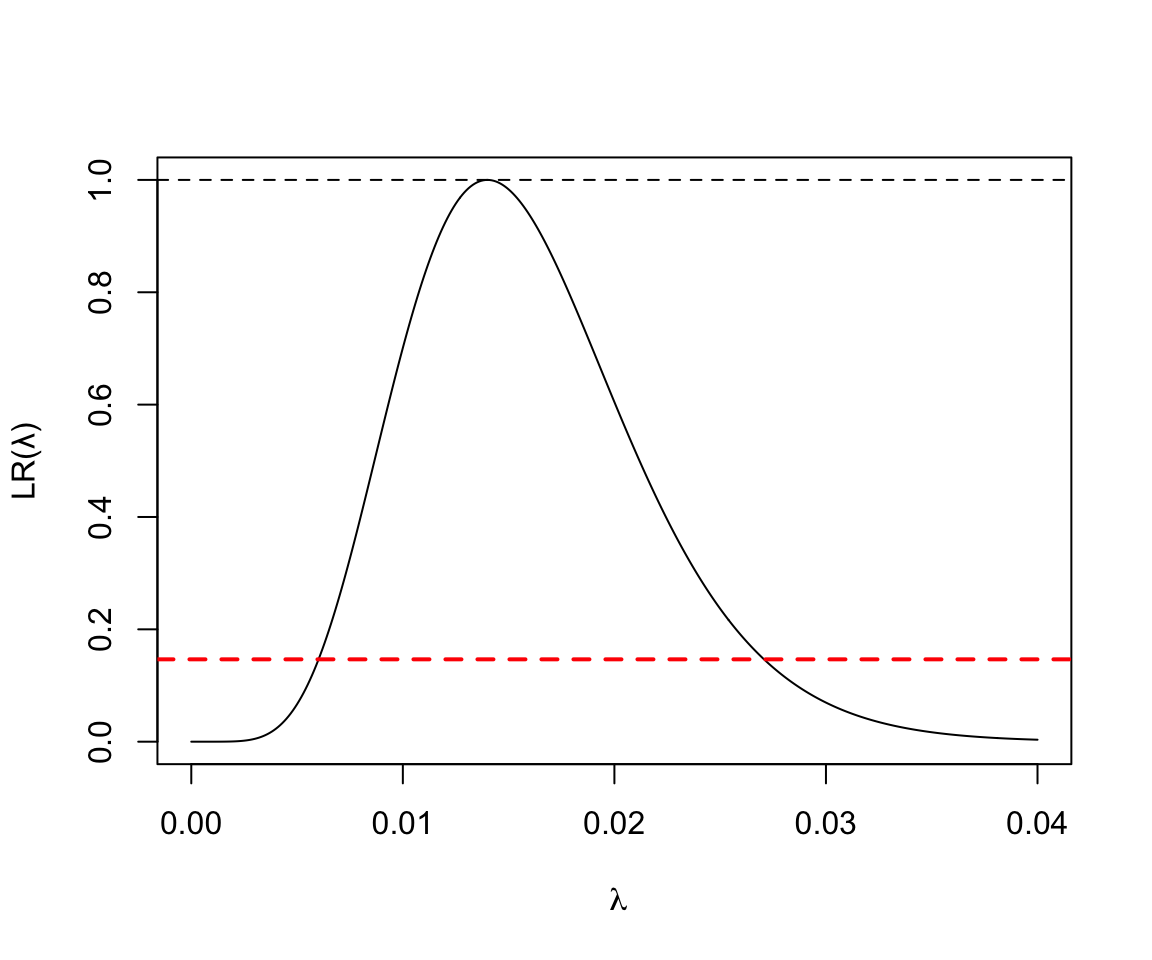
圖 119.10: Poisson Likelihood ratio for rate parameter D = 7, Y = 500
- 5000人年的觀察中發現70人死亡:
x <- seq(0, 40, by=0.01)/1000
y <- exp( -5000 * x + 70 + 70 * log( x * 5000) - 70 * log(70))
plot(x, y, type = "l", ylab = "LR(\u03BB)", xlab = ~lambda)
abline(h=1.0, lty=2)
abline(v=0.4, lty=2)
abline(h=0.1466, lty=2, lwd = 2, col = "red")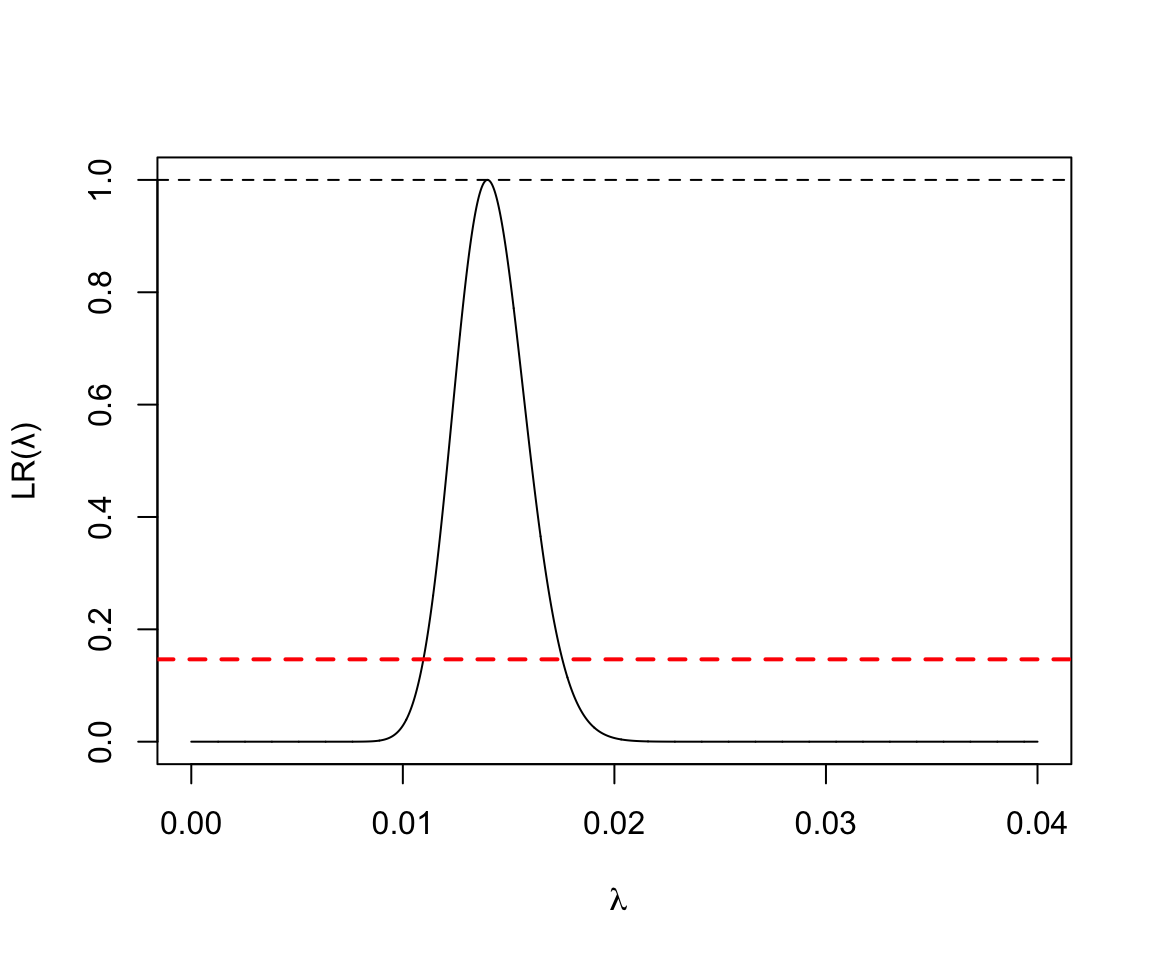
圖 119.11: Poisson Likelihood ratio for rate parameter D = 70, Y = 5000
- 50000人年的觀察中發現700人死亡:
x <- seq(0, 40, by=0.01)/1000
y <- exp( -50000 * x + 700 + 700 * log( x * 50000) - 700 * log(700))
plot(x, y, type = "l", ylab = "LR(\u03BB)", xlab = ~lambda)
abline(v=0.4, lty=2)
abline(h=1.0, lty=2)
abline(h=0.1466, lty=2, lwd = 2, col = "red")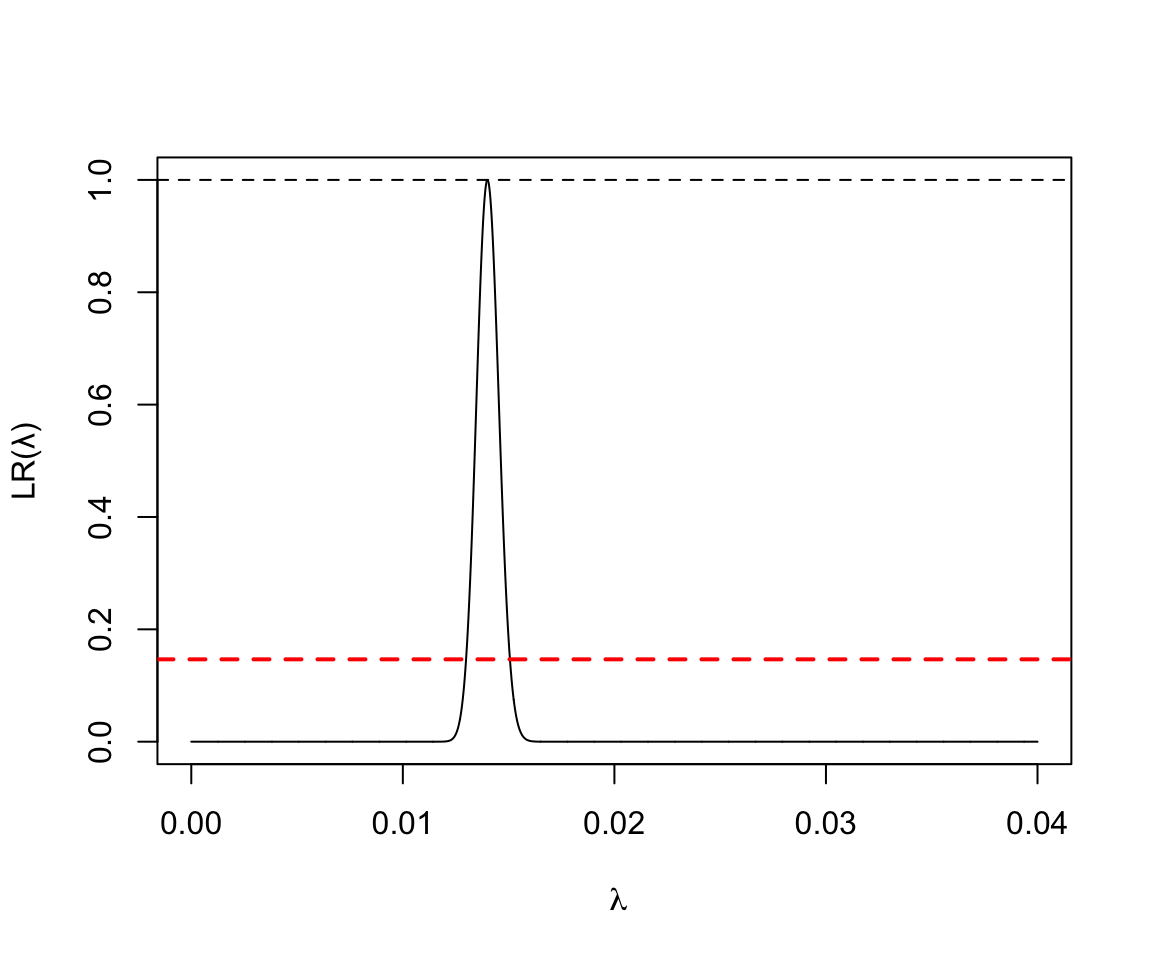
圖 119.12: Poisson Likelihood ratio for rate parameter D = 700, Y = 50000
三個圖的整體信息仍然告訴我們,數據越多,對參數的估計越精確 (more data more precise estimate)。
119.6 Q6 特別少的病例死亡的情況
當觀察到特別少, 如 1,或者 0 個病例死亡時,泊松分佈的似然函數圖形會是怎樣的?
- 500人年的觀察中發現1人死亡:
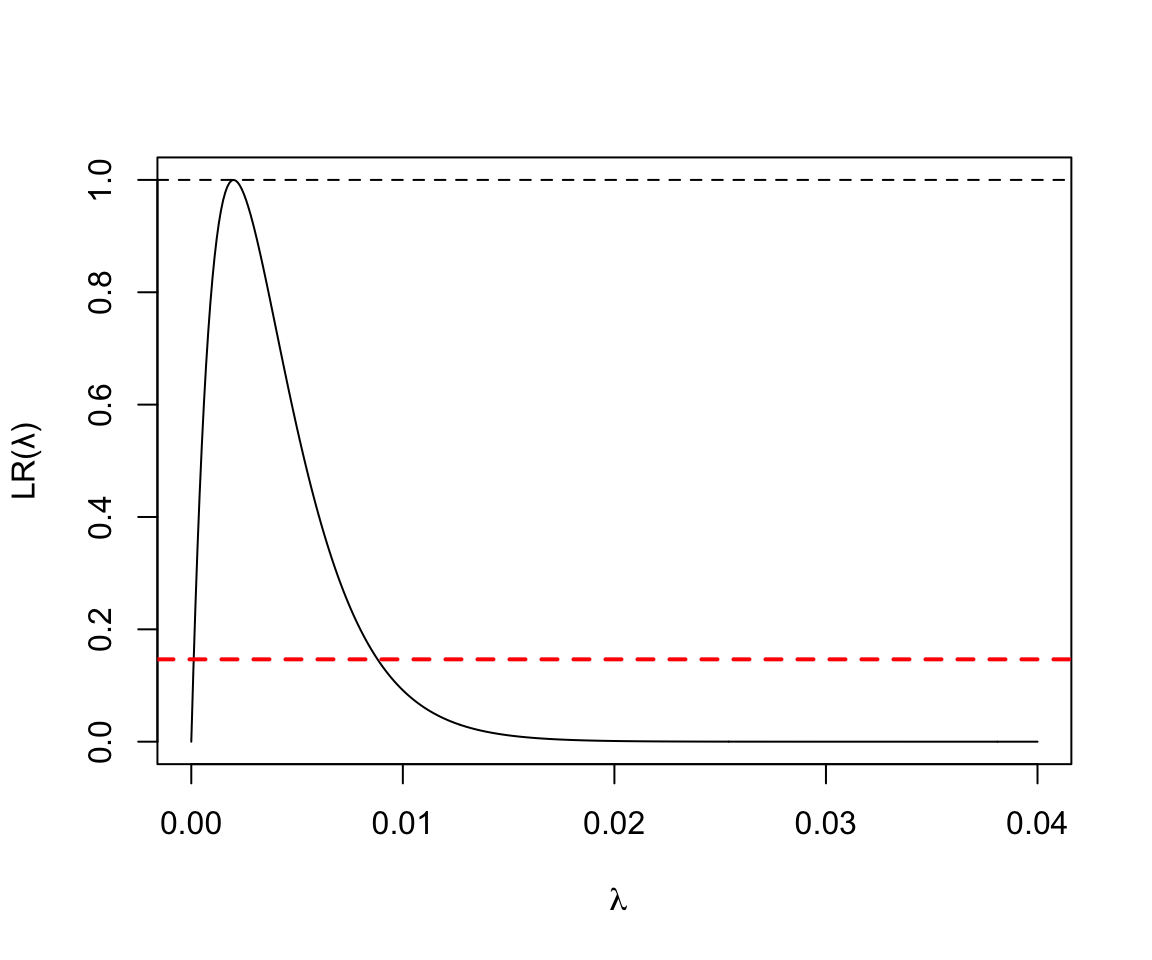
圖 119.13: Poisson Likelihood ratio for rate parameter D = 1, Y = 500
- 500人年的觀察中發現0人死亡
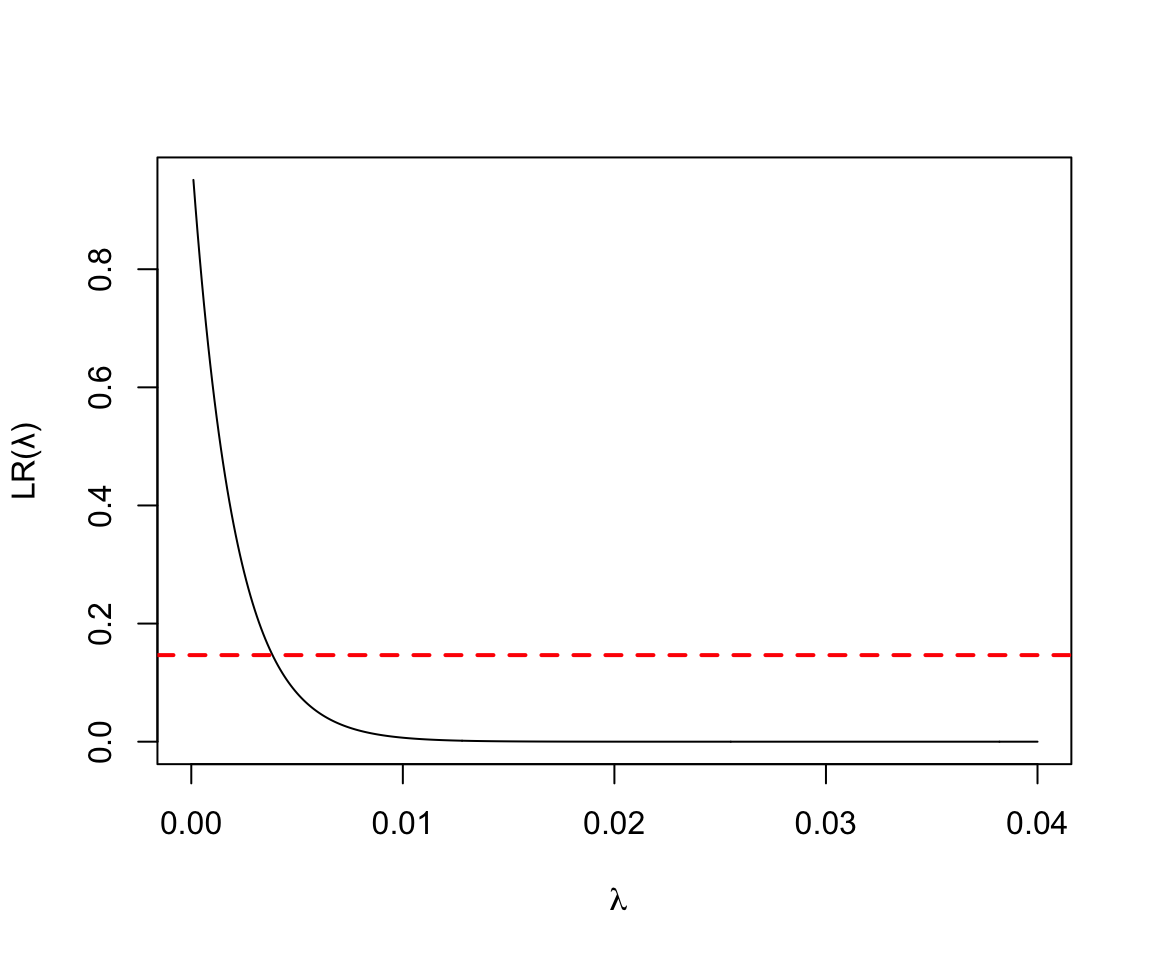
圖 119.14: Poisson Likelihood ratio for rate parameter D = 0, Y = 500
- 5000人年的觀察中發現10人死亡:
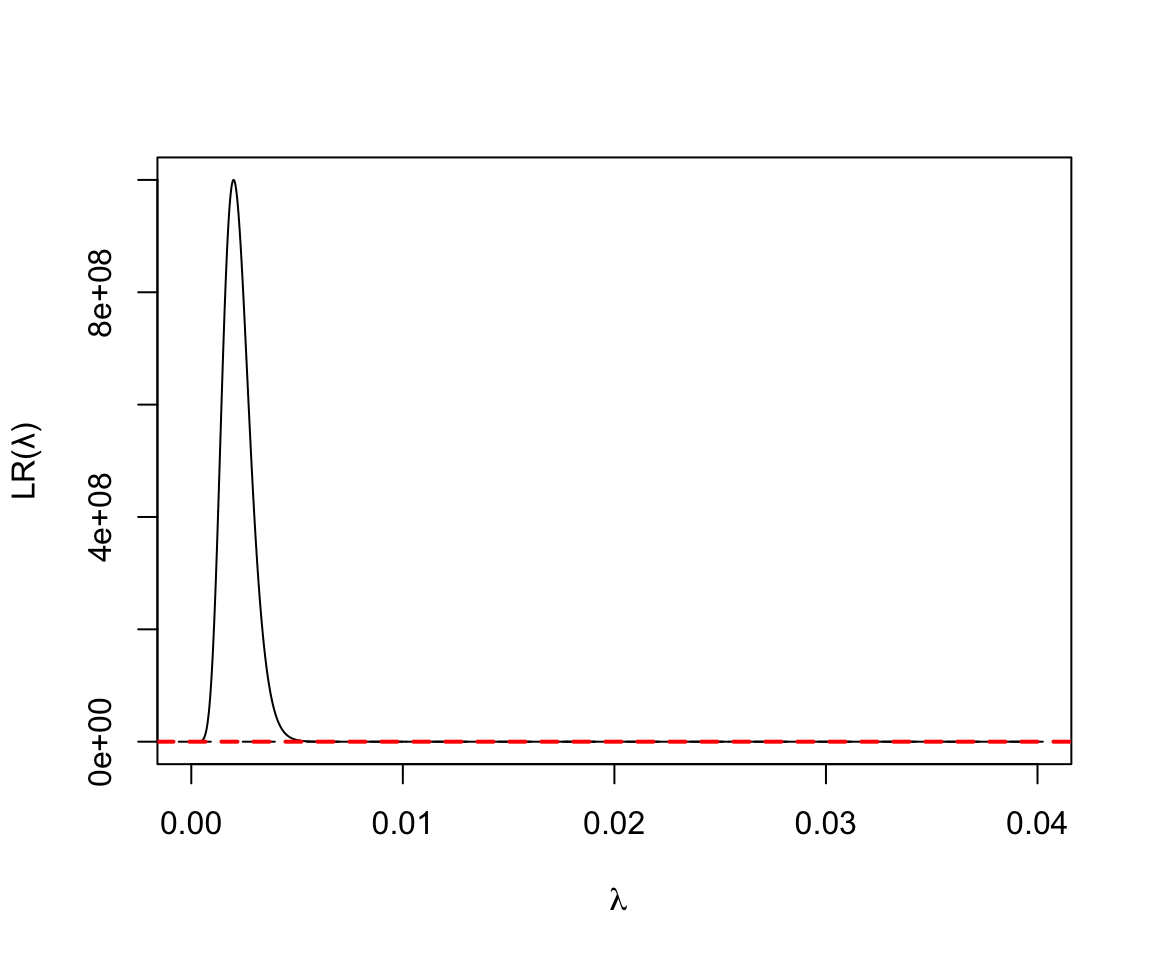
圖 119.15: Poisson Likelihood ratio for rate parameter D = 10, Y = 5000
- 5000人年的觀察中發現1人死亡:
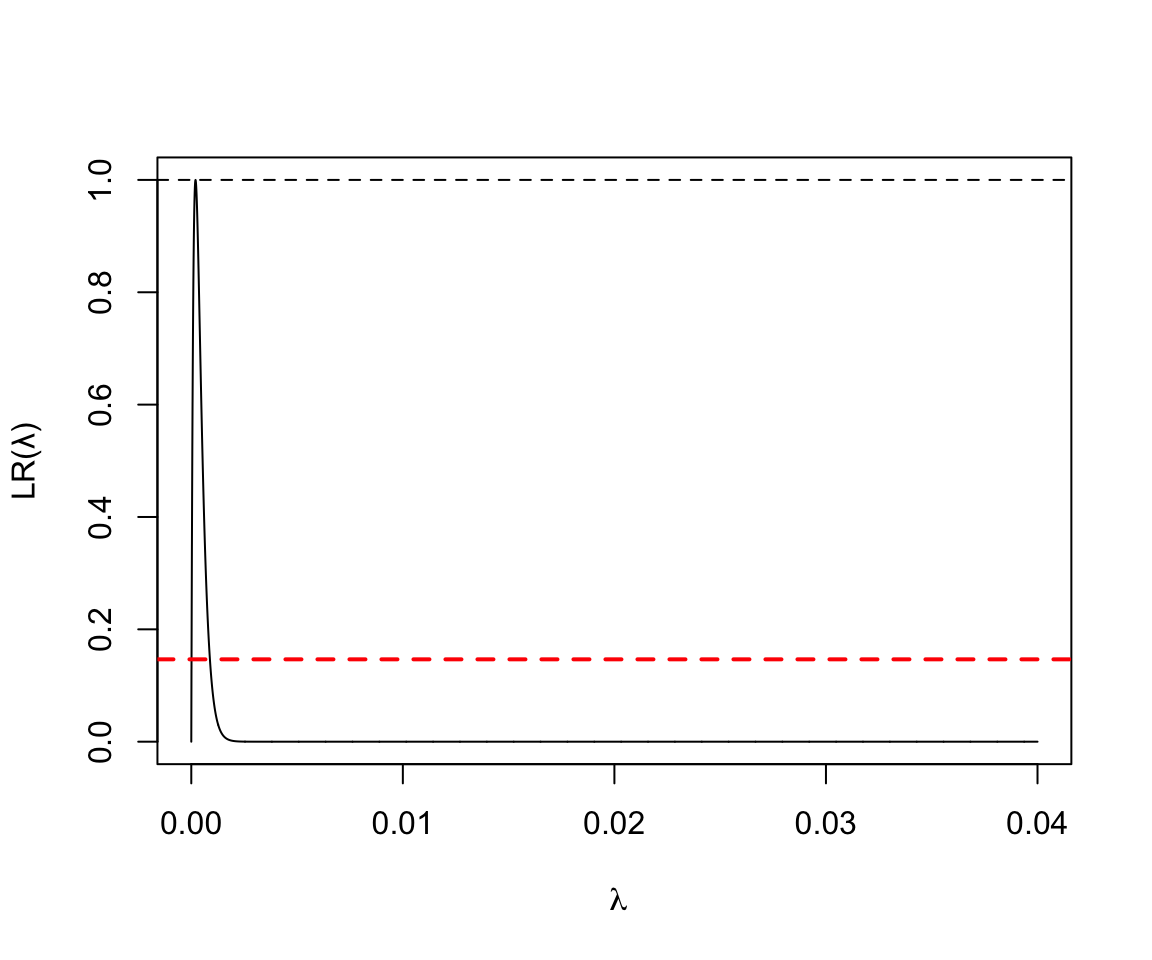
圖 119.16: Poisson Likelihood ratio for rate parameter D = 1, Y = 5000
和二項分佈時觀察到的結果一樣,當觀察值極端低的話,我們得到的似然函數的曲線就不再是左右對稱的類似正(常)態分佈的曲線了。
119.7 Q7 25人中15人選A
假如令25名受試對象從 A 和 B 兩種方案中選擇一個,他們各自的決定不影響其他人的選擇。觀察到15人選A,10人選B。繪製這個命題的二項分佈似然函數曲線:
- 10次實驗中4次失敗:
x <- seq(0,1,by=0.001)
y <- (x^15)*((1-x)^10) / ((15/25)^15*(10/25)^10)
plot(x, y, type = "l", ylab = "LR(\U03C0)", xlab = "\U03C0")
abline(v=15/25, lty=2)
abline(v=0.5, lty=2, lwd = 2, col = "blue")
abline(h=1.0, lty=2)
abline(h=0.1466, lty=2, lwd = 2, col = "red")
abline(h=(0.5^15)*((1-0.5)^10) / ((15/25)^15*(10/25)^10), lty=2, lwd = 2, col = "red")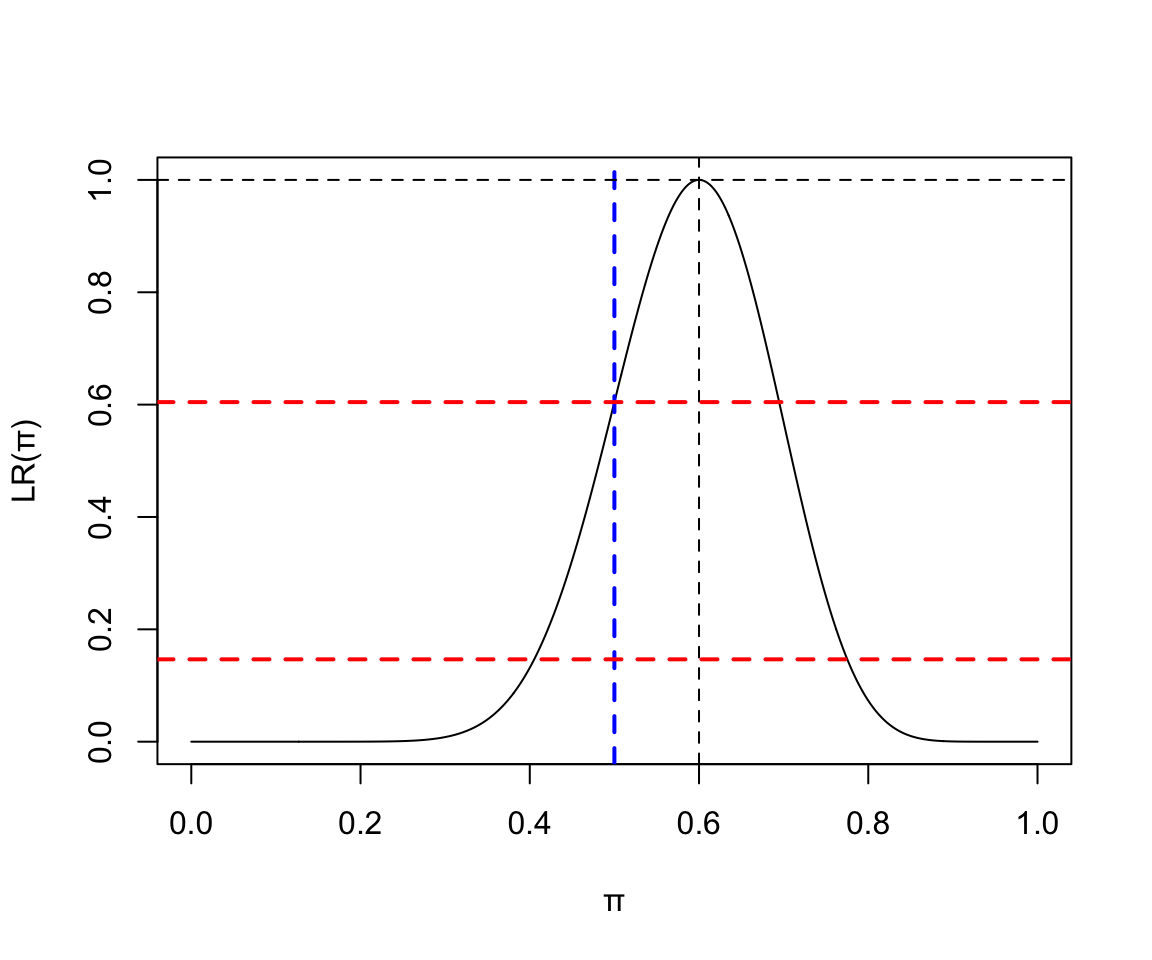
圖 119.17: Binomial(25, 15) Likelihood ratio
拿這個實驗的結果和我們認爲的零假設 “\(\pi = 0.5\),選A 和選B 的概率相同” 做假設檢驗會得到怎樣的 P 值?
##
## Exact binomial test
##
## data: 15 and 25
## number of successes = 15, number of trials = 25, p-value = 0.42436
## alternative hypothesis: true probability of success is not equal to 0.5
## 95 percent confidence interval:
## 0.38665350 0.78874519
## sample estimates:
## probability of success
## 0.6## [1] 0.60447931119.8 Q8 40人中24人選A
x <- seq(0,1,by=0.001)
y <- (x^24)*((1-x)^16) / ((24/40)^24*(16/40)^16)
plot(x, y, type = "l", ylab = "LR(\U03C0)", xlab = "\U03C0")
abline(v=24/40, lty=2)
abline(v=0.5, lty=2, lwd = 2, col = "blue")
abline(h=1.0, lty=2)
abline(h=0.1466, lty=2, lwd = 2, col = "red")
abline(h=(0.5^24)*((1-0.5)^16) / ((24/40)^24*(16/40)^16), lty=2, lwd = 2, col = "red")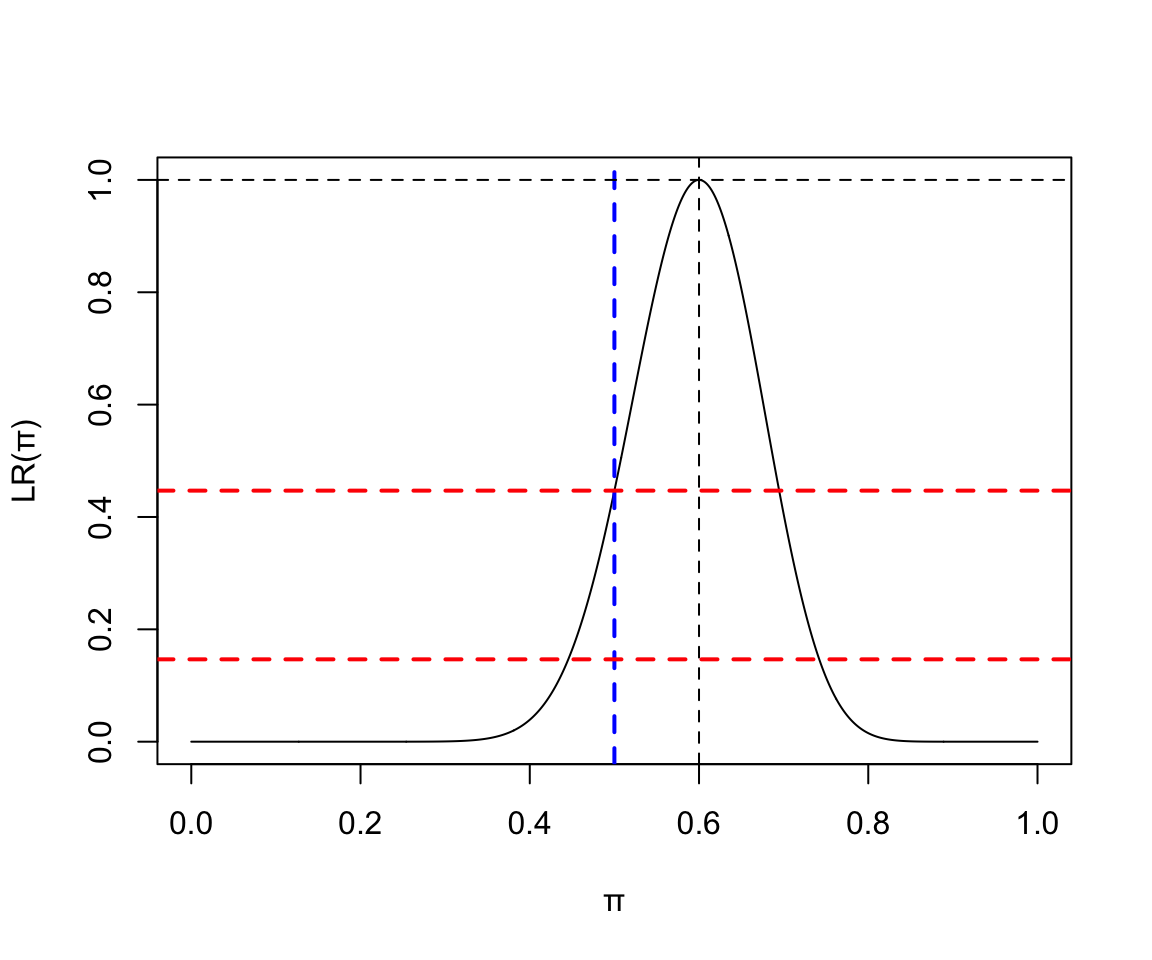
圖 119.18: Binomial(40, 24) Likelihood ratio
和相同的零假設做檢驗。
##
## Exact binomial test
##
## data: 24 and 40
## number of successes = 24, number of trials = 40, p-value = 0.26819
## alternative hypothesis: true probability of success is not equal to 0.5
## 95 percent confidence interval:
## 0.43326705 0.75135001
## sample estimates:
## probability of success
## 0.6## [1] 0.44689995119.9 Q9 60人中36人選A
x <- seq(0,1,by=0.001)
y <- (x^36)*((1-x)^24) / ((36/60)^36*(24/60)^24)
plot(x, y, type = "l", ylab = "LR(\U03C0)", xlab = "\U03C0")
abline(v=36/60, lty=2)
abline(v=0.5, lty=2, lwd = 2, col = "blue")
abline(h=1.0, lty=2)
abline(h=0.1466, lty=2, lwd = 2, col = "red")
abline(h=(0.5^36)*((1-0.5)^24) / ((36/60)^36*(24/60)^24), lty=2, lwd = 2, col = "red")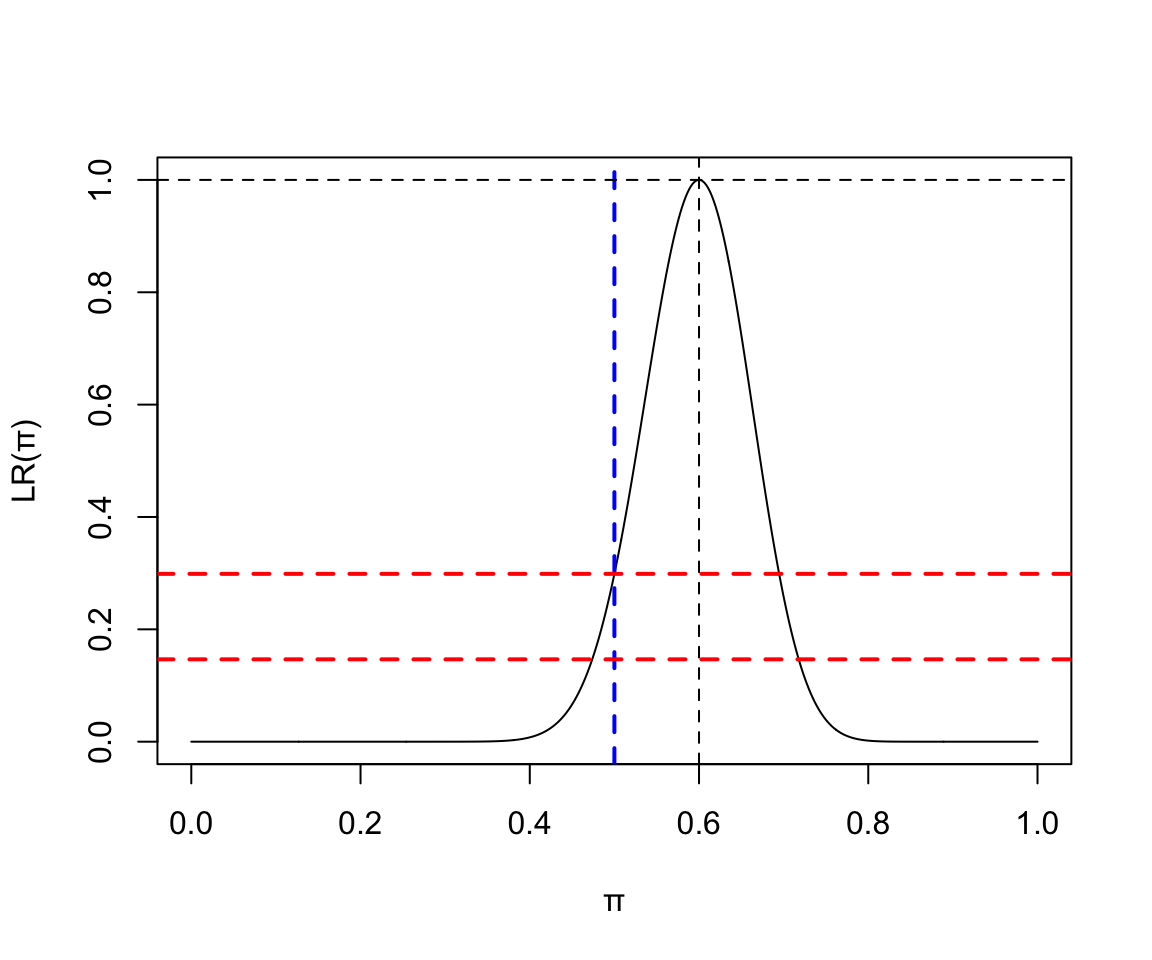
圖 119.19: Binomial(25, 15) Likelihood ratio
和相同的零假設做檢驗。
##
## Exact binomial test
##
## data: 36 and 60
## number of successes = 36, number of trials = 60, p-value = 0.155
## alternative hypothesis: true probability of success is not equal to 0.5
## 95 percent confidence interval:
## 0.46540544 0.72437842
## sample estimates:
## probability of success
## 0.6## [1] 0.29875519我們發現,當觀察數值的 \(\hat{\pi} = 0.6\) 保持不變,但數據量越多,p值就變得越小。
119.10 Q10 繪製精確 exact 和 近似 approximate 對數似然比函數
- 假設10名患者有4人最終死亡,繪製該實驗的精確對數似然比,和近似對數似然比函數圖
par(mai = c(1.2, 0.5, 1, 0.7))
pi <- seq(0.05, 0.9, by=0.001)
L <- (pi^4)*((1-pi)^6)
Lmax <- rep(max(L), length(pi))
LR <- L/Lmax
logLR <- log(LR)
# the exact binomial log likelihood ratio
plot(pi, logLR, type = "l", col = "red", ylim = c(-5, 0), yaxt="n",
ylab = "logLR(\U03C0)", xlab = "\U03C0")
# the approximate quadratic binomial log-likelihood ratio
quad <- -(pi-0.4)^2/(2*0.024)
lines(pi, quad, col="blue")
grid(NA, 5, lwd = 2) # add some horizontal grid on the background
axis(2, at=seq(-5,0,1), las=2)
axis(4, at=-1.92, las=2)
abline(h=-1.92, lty=1, col="red")
legend(x=0.15, y= -4.5 ,xpd = TRUE, legend=c("exact logLR","Quadratic approx"), bty = "n",
col=c("red","blue"), lty=c(1,1), horiz = TRUE)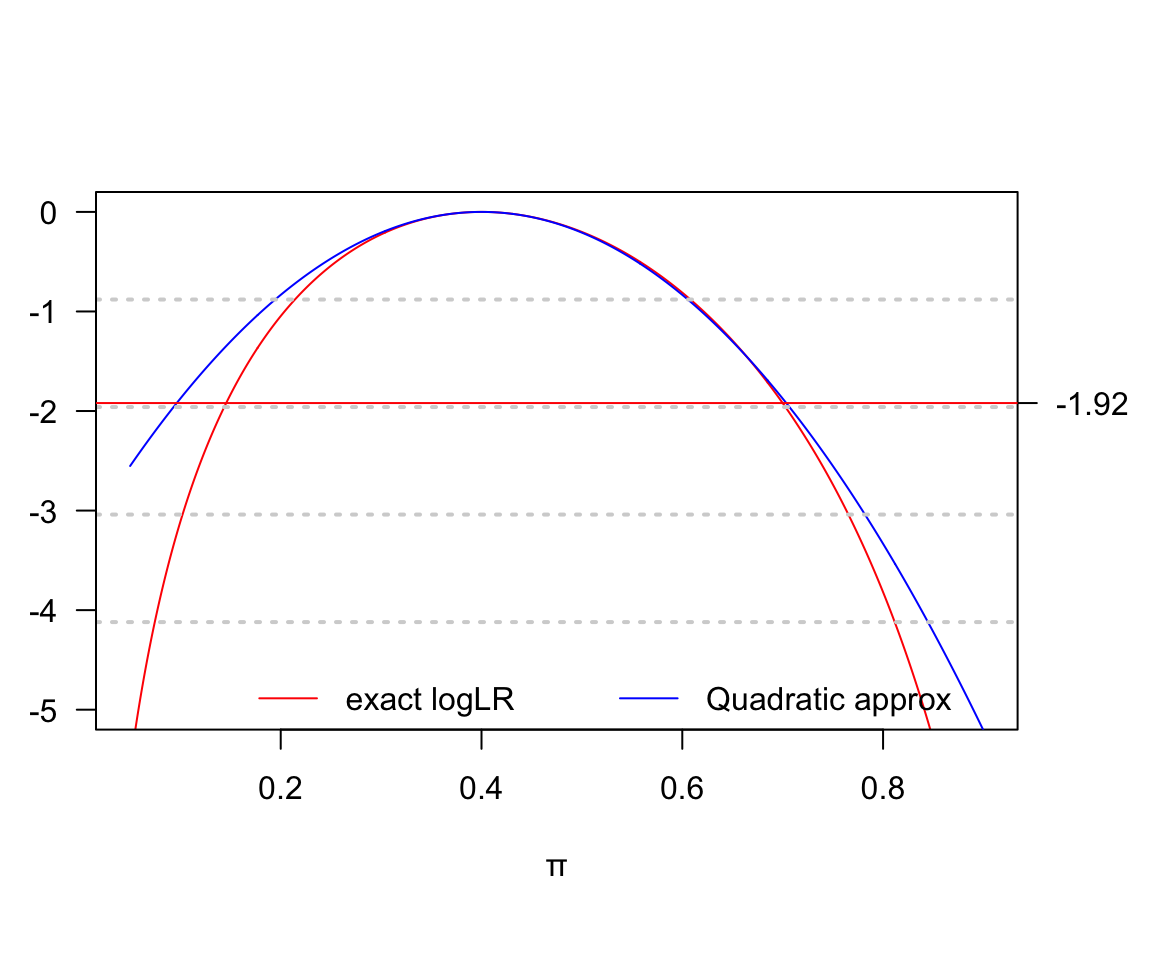
圖 119.20: Log likelihood for risk parameter: D = 4, H = 6
即便是只有10個觀察值的二項分佈數據,使用二次方程近似法給出的結果也較爲接近精確值。
119.11 Q11 繼續繪製精確 exact 和近似 approximate 對數似然比函數
- 假設另一個實驗有100名受試者,其中40人死亡,繪製該實驗的精確對數似然,和近似對數似然函數圖
par(mai = c(1.2, 0.5, 1, 0.7))
pi <- seq(0.05, 0.9, by=0.001)
L <- (pi^40)*((1-pi)^60)
Lmax <- rep(max(L), length(pi))
LR <- L/Lmax
logLR <- log(LR)
# the exact binomial log likelihood ratio
plot(pi, logLR, type = "l", col = "red", ylim = c(-5, 0), yaxt="n",
ylab = "logLR(\U03C0)", xlab = "\U03C0")
# the approximate quadratic binomial log-likelihood ratio
quad <- -(pi-0.4)^2/(2*0.0024)
lines(pi, quad, col="blue")
grid(NA, 5, lwd = 2) # add some horizontal grid on the background
axis(2, at=seq(-5,0,1), las=2)
axis(4, at=-1.92, las=2)
abline(h=-1.92, lty=1, col="red")
legend(x=0.5, y= -0.5 ,xpd = TRUE, legend=c("exact logLR","Quadratic approx"), bty = "n",
col=c("red","blue"),, lty=c(1,1), horiz = TRUE)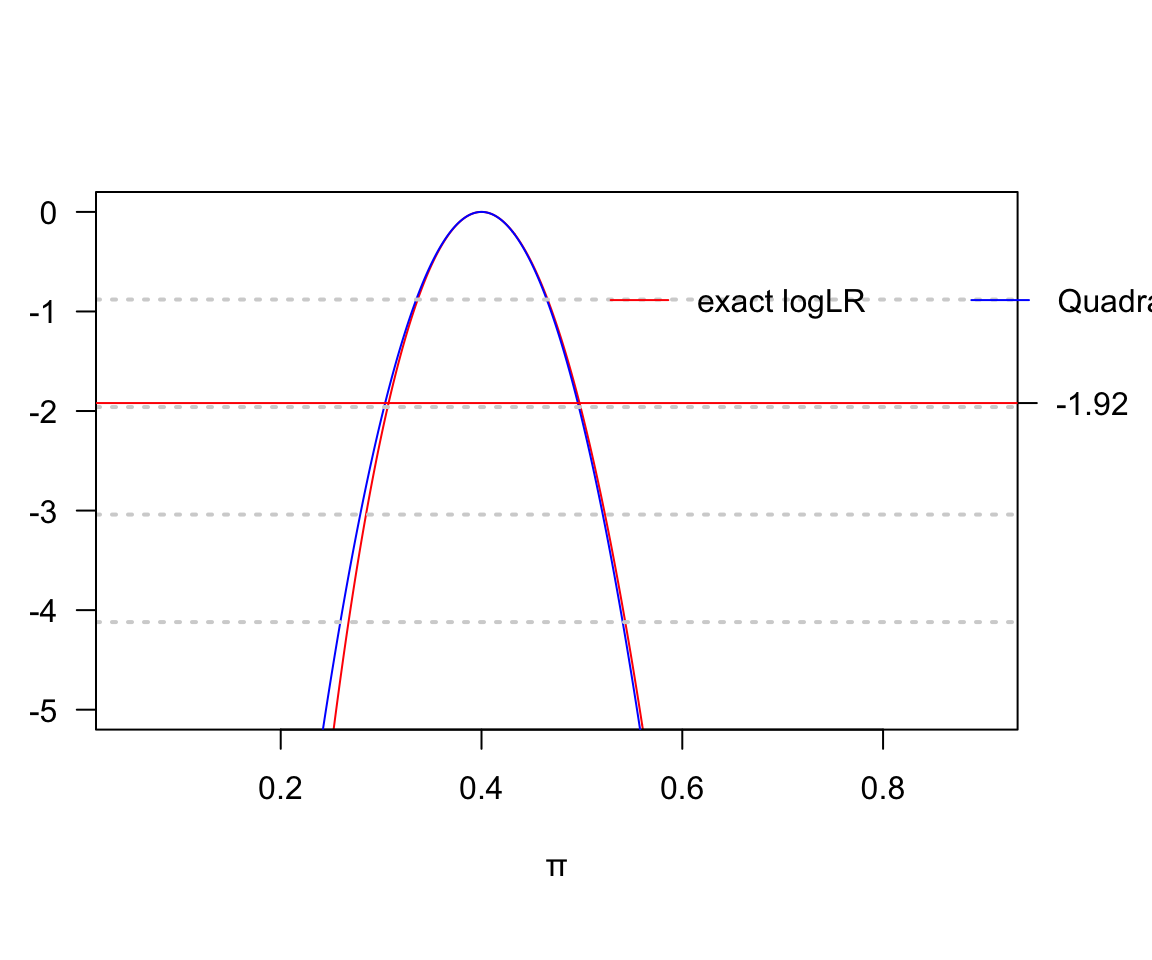
圖 119.21: Log likelihood for risk parameter: D = 40, H = 60
可以看見二次方程近似法和精確法計算的對數似然比函數在受試對象達到100人時已經十分接近。
119.12 Q12 繼續繪製精確 exact 和 近似 approximate 對數似然比函數
- 假設另一個實驗有1000名受試者,其中400人死亡,繪製該實驗的精確對數似然,和近似對數似然函數圖
par(mai = c(1.2, 0.5, 1, 0.7))
pi <- seq(0.05, 0.9, by=0.001)
L <- (pi^400)*((1-pi)^600)
Lmax <- rep(max(L), length(pi))
LR <- L/Lmax
logLR <- log(LR)
# the exact binomial log likelihood ratio
plot(pi, logLR, type = "l", col = "red", ylim = c(-5, 0), yaxt="n",
ylab = "logLR(\U03C0)", xlab = "\U03C0")
# the approximate quadratic binomial log-likelihood ratio
quad <- -(pi-0.4)^2/(2*0.00024)
lines(pi, quad, col="blue")
grid(NA, 5, lwd = 2) # add some horizontal grid on the background
axis(2, at=seq(-5,0,1), las=2)
axis(4, at=-1.92, las=2)
abline(h=-1.92, lty=1, col="red")
legend(x=0.5, y= -0.5 ,xpd = TRUE, legend=c("exact logLR","Quadratic approx"), bty = "n",
col=c("red","blue"),, lty=c(1,1), horiz = TRUE)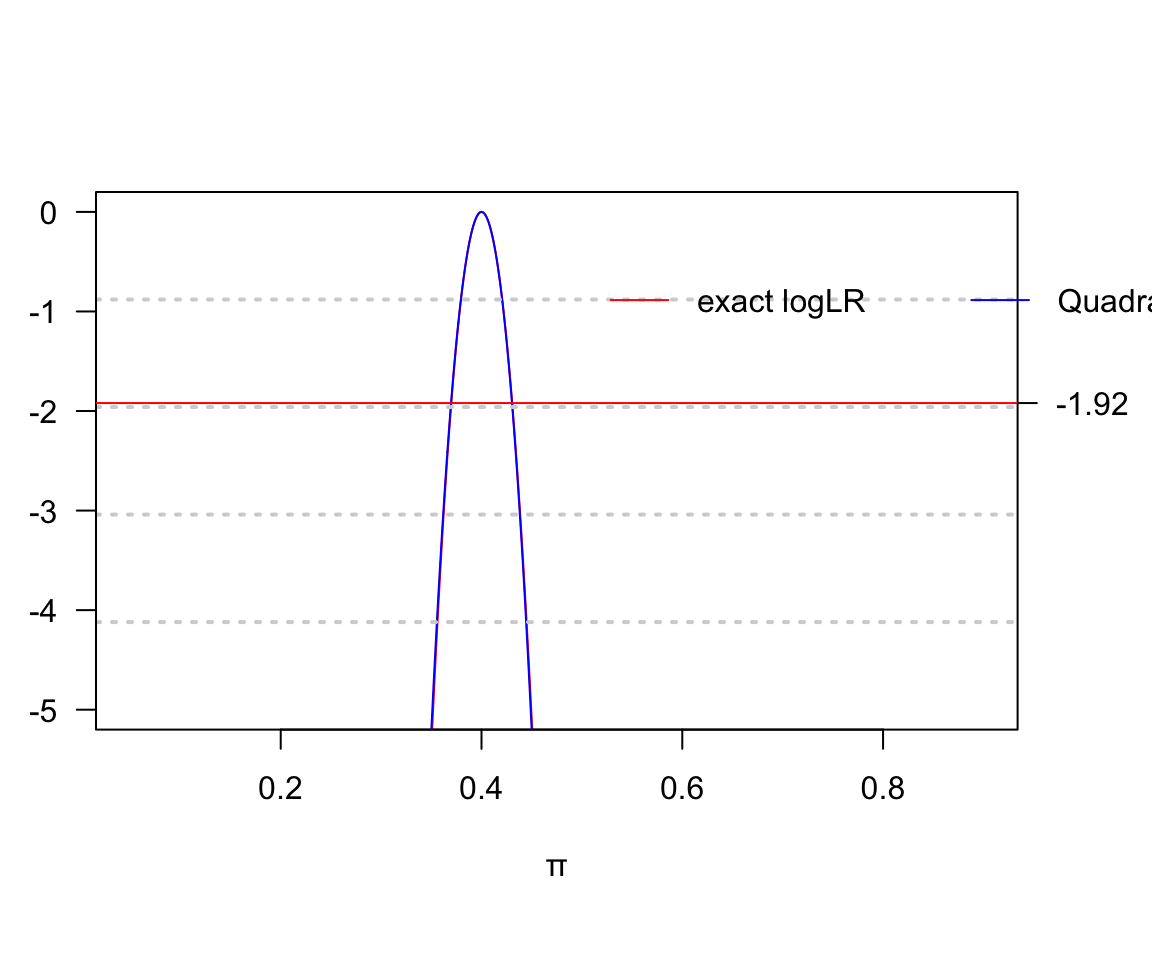
圖 119.22: Log likelihood for risk parameter: D = 40, H = 60
這裏當實驗受試對象人數爲1000人時,精確法和二次方程近似法給出的對數似然比函數曲線已經接近完美重疊。
119.13 Q13 2人死亡18人存活的實驗
- 假設此次實驗受試對象有20人,只有2人死亡的結果的時候的二項分佈對數似然比函數(精確法和近似法)
par(mai = c(1.2, 0.5, 1, 0.7))
pi <- seq(0, 0.3, by=0.0001)
L <- (pi^2)*((1-pi)^18)
Lmax <- rep(max(L), length(pi))
LR <- L/Lmax
logLR <- log(LR)
# the exact binomial log likelihood ratio
plot(pi, logLR, type = "l", col = "red", ylim = c(-5, 0), yaxt="n",
ylab = "logLR(\U03C0)", xlab = "\U03C0")
# the approximate quadratic binomial log-likelihood ratio
quad <- -(pi-0.1)^2/(2*(0.1*0.9/20))
lines(pi, quad, col="blue")
grid(NA, 5, lwd = 2) # add some horizontal grid on the background
axis(2, at=seq(-5,0,1), las=2)
axis(4, at=-1.92, las=2)
abline(h=-1.92, lty=1, col="red")
legend(x=0.1, y= -4.2 ,xpd = TRUE, legend=c("exact logLR","Quadratic approx"), bty = "n",
col=c("red","blue"), lty=c(1,1), horiz = TRUE)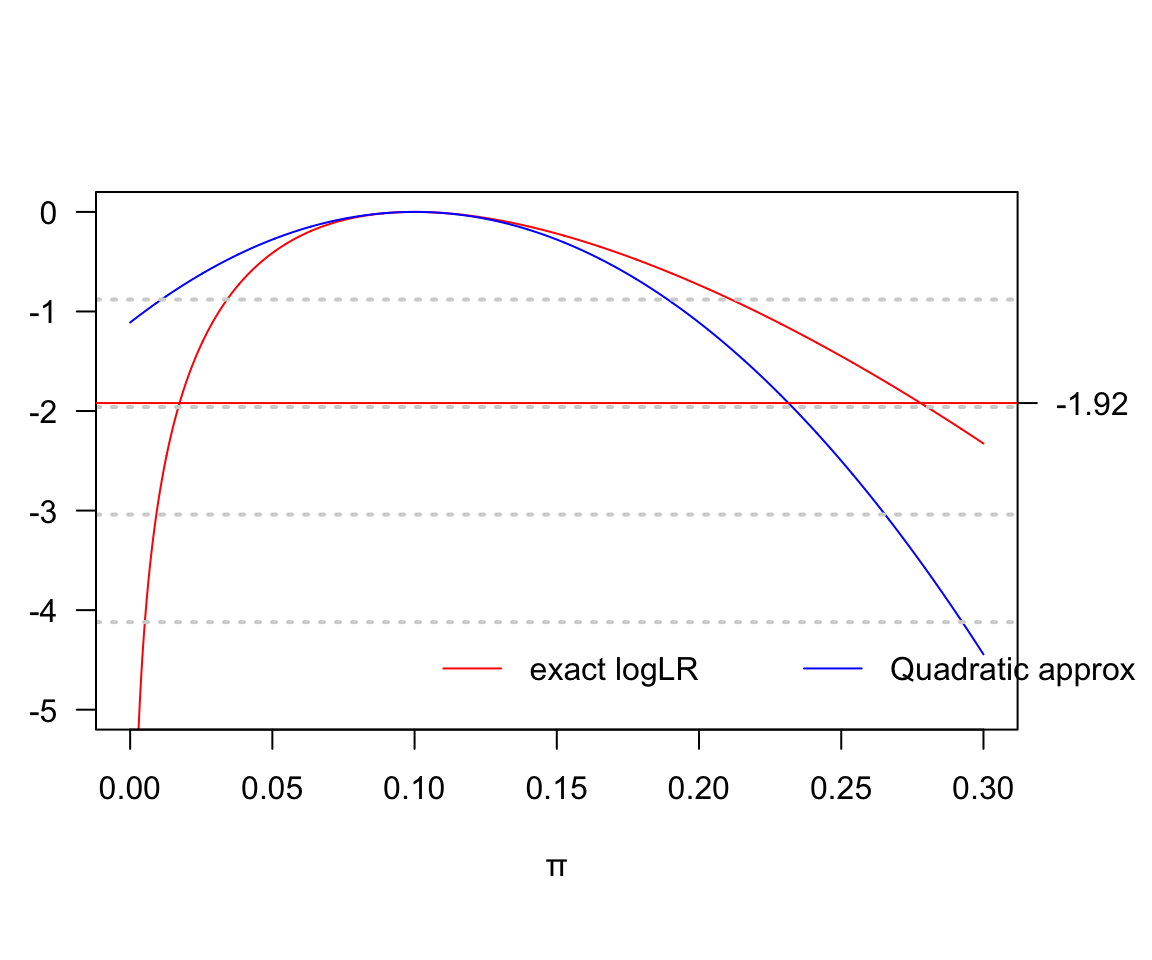
圖 119.23: Log likelihood for risk parameter: D = 2, H = 18
這裏我們看見20人這一較小的實驗規模中,如果出現了只有2個死亡病例的情況下,近似法和精確法之間的差別很大。而且近似法給出的藍色曲線的95%信賴區間的下限甚至是負的。
- 假設總人數是200人,觀察到了20人死亡的話,我們再來看看此時的對數似然比函數圖
par(mai = c(1.2, 0.5, 1, 0.7))
pi <- seq(0, 0.3, by=0.0001)
L <- (pi^20)*((1-pi)^180)
Lmax <- rep(max(L), length(pi))
LR <- L/Lmax
logLR <- log(LR)
# the exact binomial log likelihood ratio
plot(pi, logLR, type = "l", col = "red", ylim = c(-5, 0), yaxt="n",
ylab = "logLR(\U03C0)", xlab = "\U03C0")
# the approximate quadratic binomial log-likelihood ratio
quad <- -(pi-0.1)^2/(2*(0.1*0.9/200))
lines(pi, quad, col="blue")
grid(NA, 5, lwd = 2) # add some horizontal grid on the background
axis(2, at=seq(-5,0,1), las=2)
axis(4, at=-1.92, las=2)
abline(h=-1.92, lty=1, col="red")
legend(x=0.13, y= 0 ,xpd = TRUE, legend=c("exact logLR","Quadratic approx"), bty = "n",
col=c("red","blue"), lty=c(1,1), horiz = TRUE)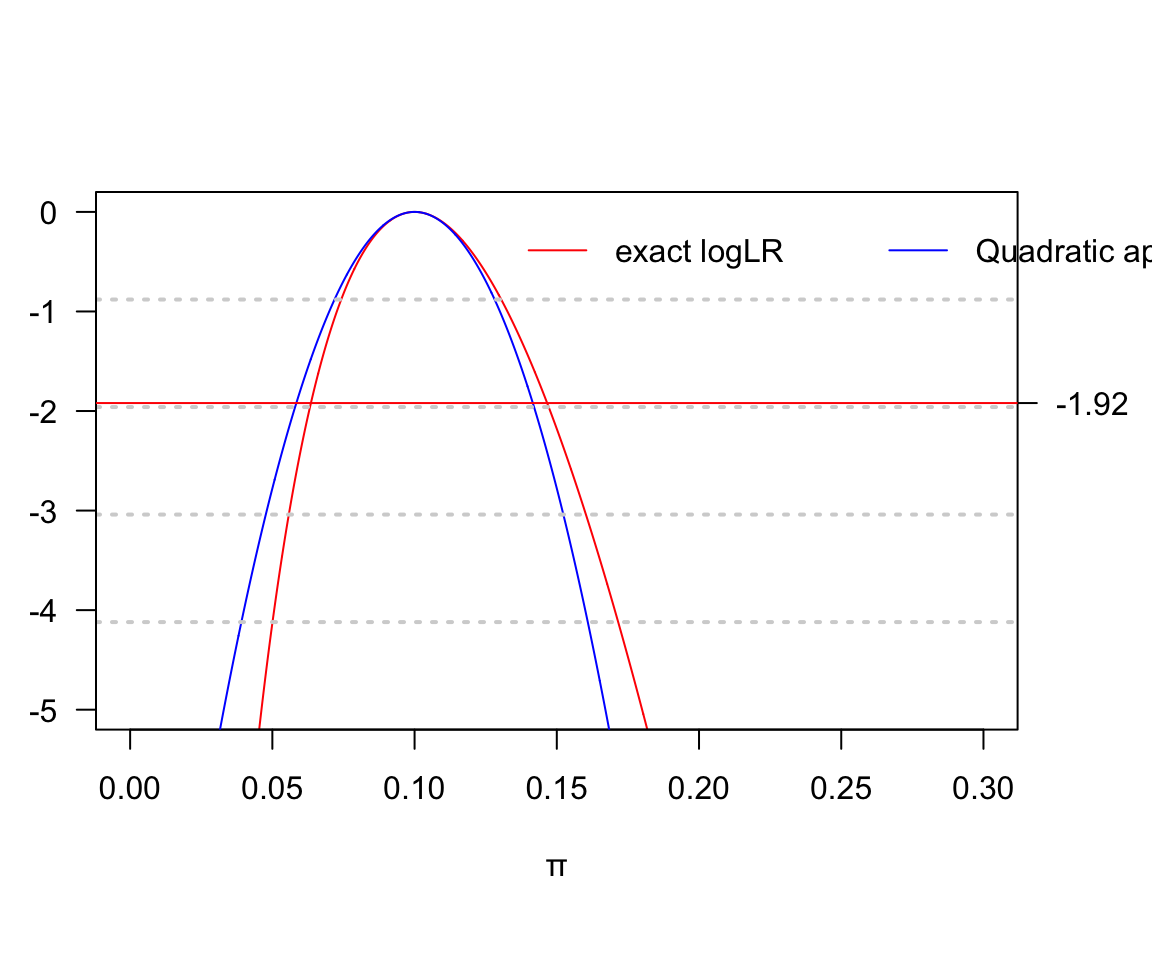
圖 119.24: Log likelihood for risk parameter: D = 20, H = 180
此時由於總體人數增多,雖然產生死亡的病例比例和之前相同,但是此時的二次方程近似法也給出了比之前較爲可以接受的近似曲線。也不會出現負的信賴區間下限的問題。
119.14 Q14 對數比值 logodds 的對數似然比函數
但是如果不是用百分比而是轉而使用對數比值 logodds 的話,我們發現近似法在對數比值尺度上也能避免出現負的信賴區間下限的問題。
. bloglik 2 18, logodds
Most likely value for logodds parameter -2.19722
cut-point -1.921
Likelihood based limits for logodds parameter -4.03622 -0.95459
Approx quadratic limits for logodds parameter -3.65820 -0.73625
Back on original risk scale
Most likely value for risk parameter 0.10000
Likelihood based limits for risk parameter 0.01736 0.27796
Approx quadratic limits for risk parameter 0.02513 0.32382
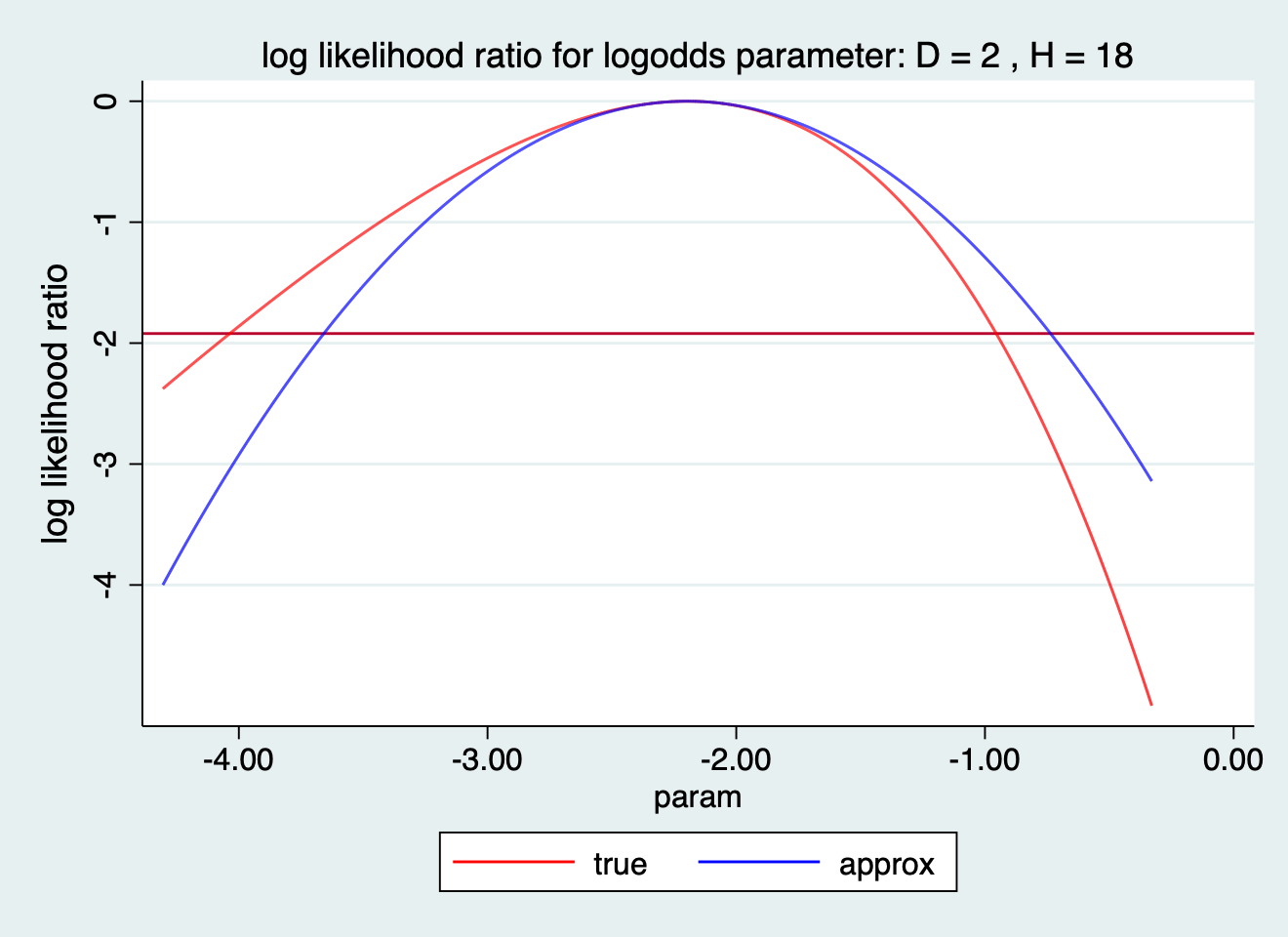
圖 119.25: log likelihood ratio for logodds paramter: D=2 H=18
119.15 Q15 繪製泊松分佈的對數似然比函數
- 假設實驗對象的觀察時間達是 500 人年 (person-year),觀察到了7人死亡的結果。此時的泊松分佈對數似然比函數是怎樣的?
泊松分佈的二次方程近似法:
$$ \[\begin{aligned} \hat\lambda = \frac{d}{p} = M ; S^2 = \frac{d}{p^2} \\ q(\lambda) = -\frac{1}{2}(\frac{\lambda - M}{S})^2 \\ 95\%\text{CI for } \lambda = \frac{d}{p} \pm 1.96 \frac{\sqrt{d}}{p} \end{aligned}\]$$
x <- seq(3, 25, by=0.1)/1000
# exact log likelihood ratio
y <- -500 * x + 7 + 7 * log( x * 500) - 7 * log(7)
plot(x, y, type = "l", ylab = "logLR(\u03BB)", xlab = ~lambda, yaxt="n",
col = "red")
# approximate log likelihood ratio
quad <- - 0.5 *(x - 7/500)^2 / (7/500^2)
lines(x, quad, col="blue")
grid(NA, 5, lwd = 2) # add some horizontal grid on the background
axis(2, at=seq(-5,0,1), las=2)
axis(4, at=-1.92, las=2)
abline(h=-1.92, lty=2, lwd = 2, col="red")
legend(x=0.01, y= -4.6 ,xpd = TRUE, legend=c("exact logLR","Quadratic approx"), bty = "n",
col=c("red","blue"), lty=c(1,1), horiz = TRUE)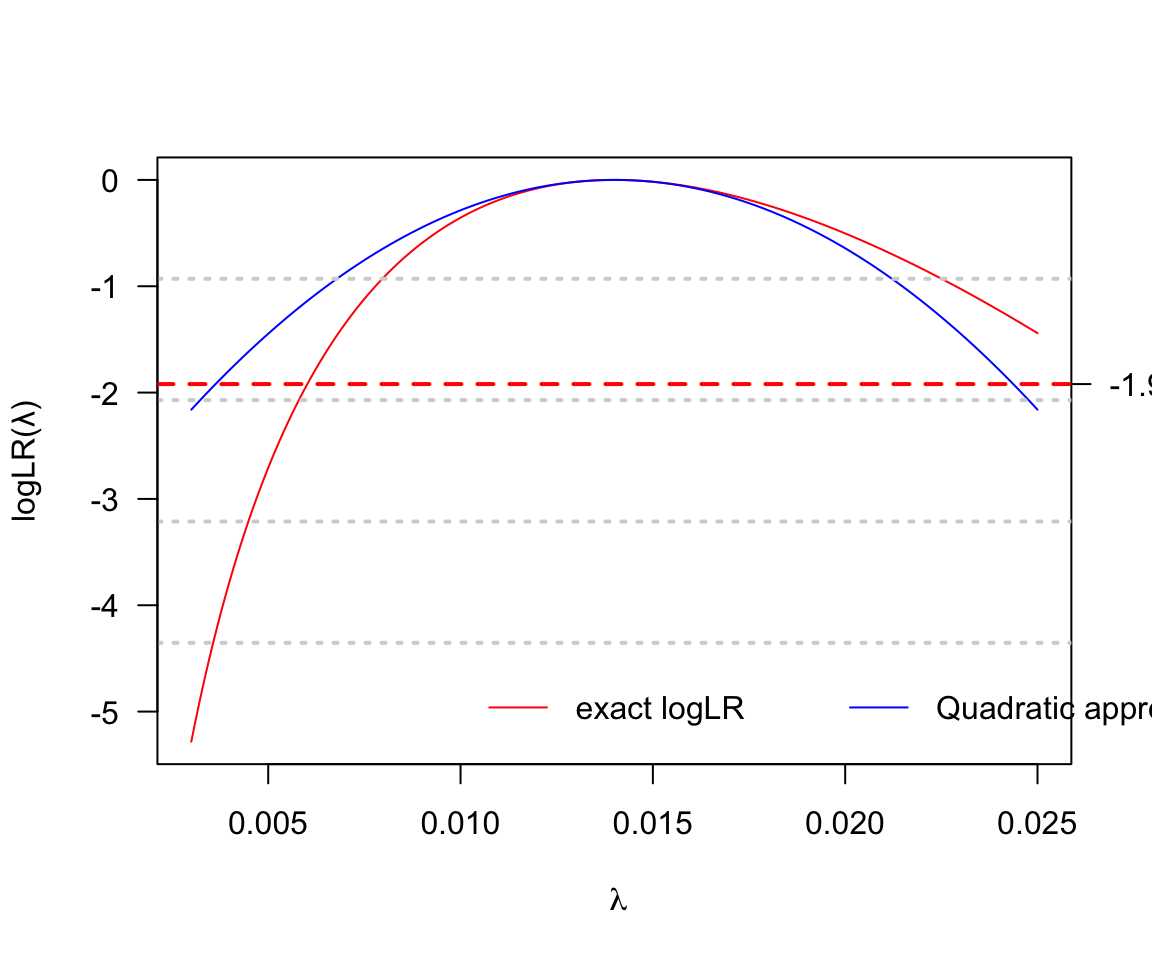
圖 119.26: Poisson Likelihood ratio for rate parameter D = 7, Y = 500
## [1] 0.0036286549## [1] 0.024371345119.16 Q16 繪製泊松分佈的對數率的對數似然比函數
. ploglik 7 500, lograte
ALL RATES PER 1000
Most likely value for log rate parameter 2.64
cut-point -1.921
Likelihood based limits for log rate parameter 1.79 3.30
Approx quadratic limits for log rate parameter 1.90 3.38
Back on original rate scale
Most likely value for rate parameter 14.00
Likelihood based limits for rate parameter 6.02 27.08
Approx quadratic limits for rate parameter 6.67 29.37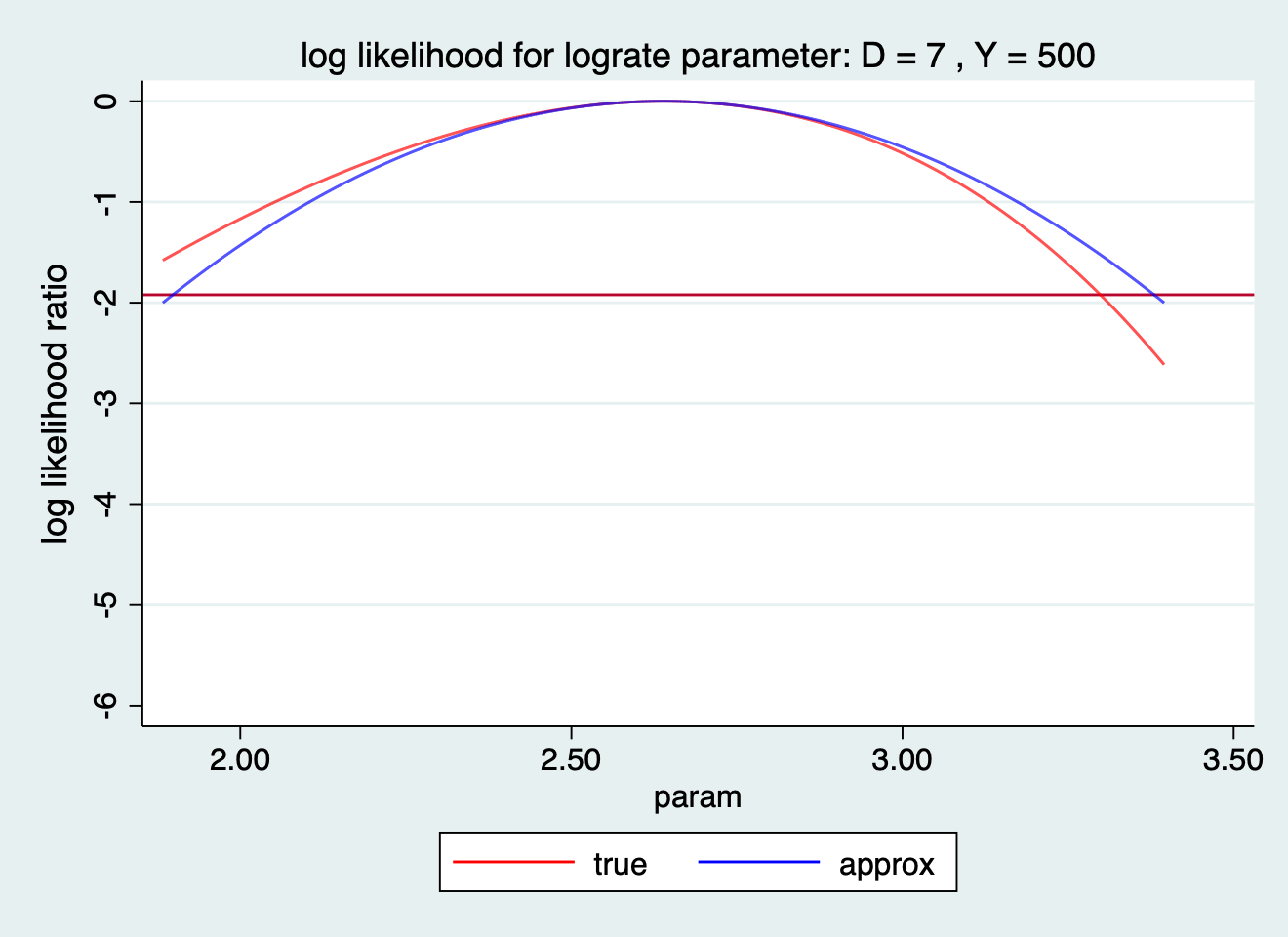
圖 119.27: log likelihood ratio for lograte paramter: D=7 Y=500
可見和比值類似,取對數以後的數值用來進行二次方程近似法給出的可信區間也比原始的率尺度更加接近“精確值”。
119.17 Q17 繪製極端情況下的泊松分佈對數似然比函數
- 原始的死亡率尺度
. ploglik 1 1000
ALL RATES PER 1000
Most likely value for rate parameter 1.00
cut-point -1.921
Likelihood based limits for rate parameter 0.06 4.40
Approx quadratic limits for rate parameter -0.96 2.96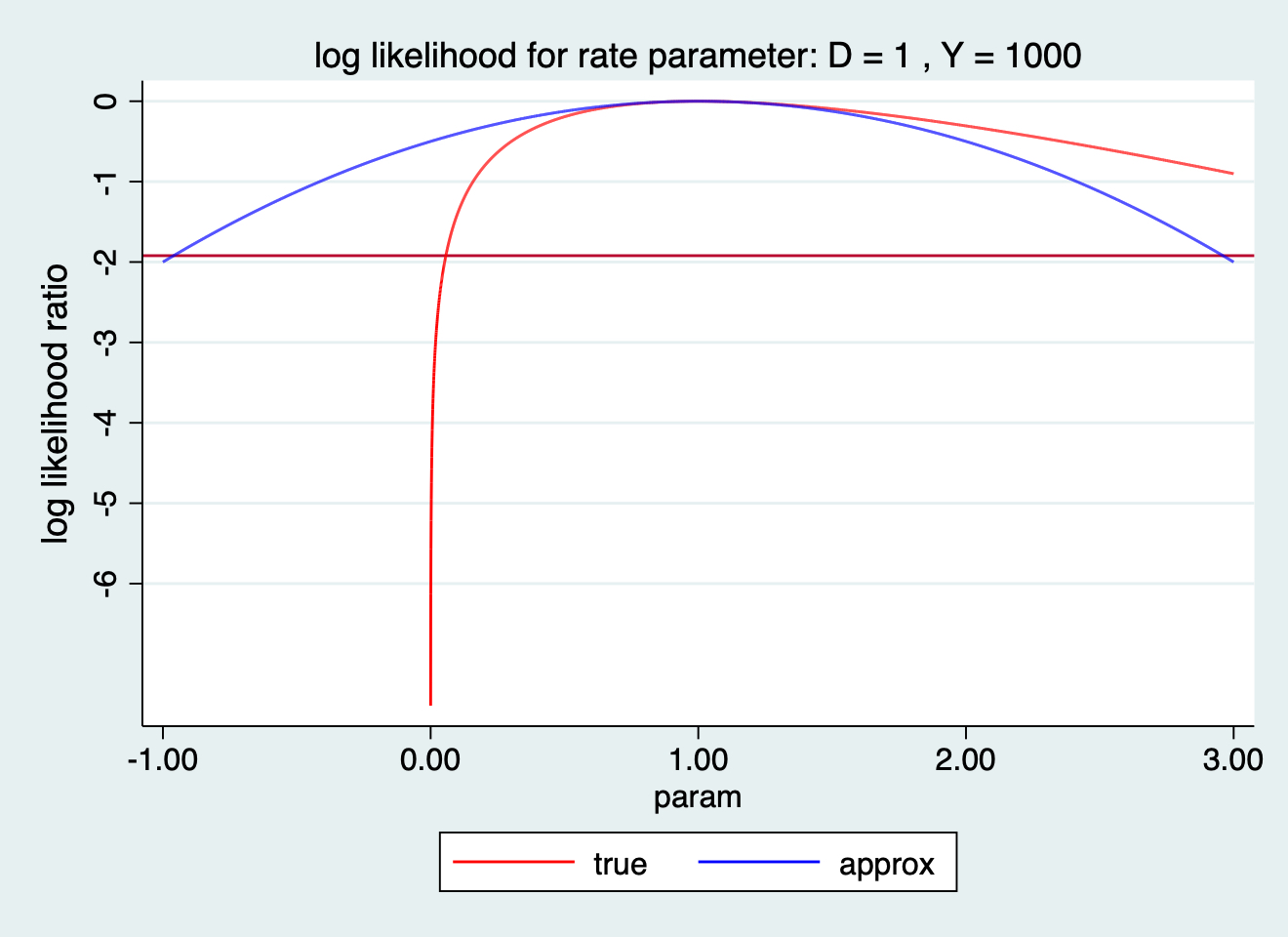
圖 119.28: log likelihood ratio for rate paramter: D=1 Y=1000
- 對數死亡率尺度
. ploglik 1 1000, lograte
ALL RATES PER 1000
Most likely value for log rate parameter 0.00
cut-point -1.921
Likelihood based limits for log rate parameter -2.86 1.48
Approx quadratic limits for log rate parameter -1.96 1.96
Back on original rate scale
Most likely value for rate parameter 1.00
Likelihood based limits for rate parameter 0.06 4.40
Approx quadratic limits for rate parameter 0.14 7.10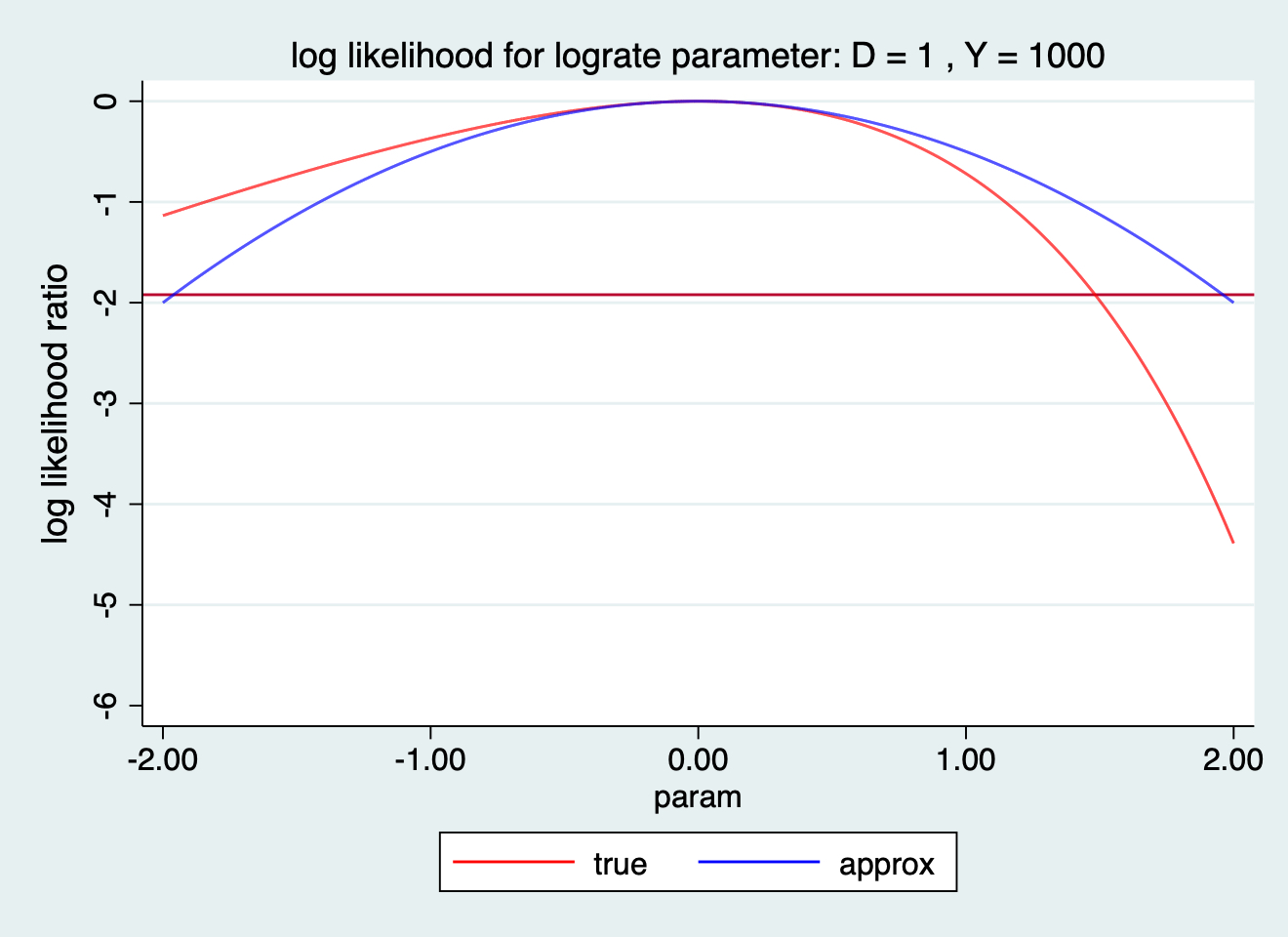
圖 119.29: log likelihood ratio for lograte paramter: D=1 Y=1000
對數尺度在泊松分佈的情況下,同樣在近似計算中避免了出現負的信賴區間下限的情況。