第 88 章 Cox 比例風險模型

88.1 本章概要

  • 學會寫下 Cox 比例風險函數的數學表達式
  • 能夠解釋 Cox 比例風險模型是怎樣通過偏似然的方法獲取 MLE 的，這個過程又是怎樣獲得估計風險度比 (hazard ratio)，和它的標準誤，p 值，以及信賴區間的
  • 比較 Cox 比例風險模型和全參數模型 (fully parametric models)，及非參數方法 (non-parametric methods)
  • 能夠解釋各種不同類型的（連續型，二進制型，或者多變量型）解釋（暴露）變量在 Cox 比例風險模型中獲得的參數估計的涵義
  • 學會使用統計軟件繪製的圖形方法來分析並解釋比例風險度的假設條件是否得到滿足
  • 能夠在 R 等統計包中準確地運行需要的 Cox 比例風險模型，並且會用這些統計包輔助進行模型性能評測

88.2 初步介紹 Cox 比例風險模型

如果可以認爲暴露（解釋）變量對風險度的作用是成比例的 (act proportionally on the hazard)，那麼對某個觀察對象來說，他/她/它的解釋變量如果用向量 \(\mathbf{X} = x\) 來表示的話，他/她/它的風險度方程和基線風險度 (baseline hazard) 之間的關係可以描述爲：

\[ h(t|x) = h_0(t)e^{\beta^Tx} \]

其中，\(h_0(t)\) 就是被比較的基線組成員(baseline individual)的風險度函數 (hazard function)，在 Weibull 模型或者指數模型中，這個基線風險 (baseline hazard) 是需要被模型根據數據來進行參數估計的 (parameterized)。但是，1972年，神一樣的人物 Cox (David R. Cox 1972) 提出，其實我們不需要對這個基線風險進行估計，可以忽略它在模型中的存在。正因為如此，這個模型被冠以發明者的名字 Cox proportional hazards model。因為此模型不對基線風險進行任何估計，但是對預測變量對於風險的效果 (effect of the explanatory variable) 用模型中的 \(\beta\) 進行參數估計，所以，它又被稱爲是半參數化模型 (semi-parametric model)。

下面的討論，我們保持和之前的章節使用相同的數學標記法。

  • \(i = 1, \dots, n\) 標記實驗對象的個體編號
  • \(x_i\) 表示她/他/它的解釋型變量（大多數情況下它是包含了多個變量的向量）
  • \(t_i\) 表示生存時間（刪失時間）
  • \(\delta_i\) 則是指示是使用生存時間，或者刪失時間的指示變量 (indicator)

那麼用這些標記法描述的 Cox 比例風險模型下的似然是：

\[ L= \prod_{i=1}^n\{ h_0(t)e^{\beta^Tx_i}\exp(-\int_0^{t_i} h_0(u)e^{\beta^Tx_i}du) \}^{\delta_i}\{ \exp(-\int_0^{t_i} h_0(u)e^{\beta^Tx_i}du) \}^{1-\delta_i} \]

是無法估計的，此時要用到偏似然法 (partial likelihood)，

88.3 偏似然法 (partial likelihood)

假定已知某一名實驗對象身上經過了生存時間 \(t_j\) 之後發生了研究者追蹤的事件 (event of interest)。我們用 \(i_j\) 標記該實驗對象，她/他/它身上具有的所有解釋變量則用 \(x_{i_j}\) 來表達。在無限接近時間點 \(t_j\) 之前的時刻，有一個包含了所有此時仍未發生事件的觀察對象的潛在對象集合 (risk set) \(R_j\)。觀察對象 \(i_j\) 也屬於這個潛在對象集合 \(R_j\)。這裏我們假定該時間無限短，短到有且僅有一個對象可以發生事件，即沒有人同時發生事件。如圖 88.1

Definition of risk sets.

圖 88.1: Definition of risk sets.

接下來我們思考這樣一個問題：在這組用 \(R_j\) 標記的潛在對象集合中，我們已知它們同時都存活到了時間點 \(t_j\)，且沒有發生刪失，那麼這組患者中的某個個體 \(i_j\)，它/他/她有一個解釋變量 \(x_i\)，它/他/她在這個時間點發生事件的條件概率 (conditional probability) 該怎麼計算？

\[ \frac{h_0(t_j)\exp(\beta^Tx_{i_j})}{\sum_{k\in R_j}h_0(t_j)\exp(\beta^Tx_k)} = \frac{\exp(\beta^Tx_{i_j})}{\sum_{k\in R_j}\exp(\beta^Tx_k)} \]

是的，你沒有看錯，基線風險度 \(h_0(t)\) 被完美的從分子和分母中抵消掉了，這就是它不需要被參數估計的原因。那麼，在所有發生事件的時間點上，我們都可以類似的計算其對應的條件概率，然後把所有發生事件時的條件概率相乘，就獲得了我們所需要的偏似然 (partial likelihood)，用 \(L_p\) 來表示：

\[ L_p = \prod_j \frac{\exp(\beta^Tx_{i_j})}{\sum_{k\in R_j}\exp(\beta^Tx_k)} \]

這個似然之所以被命名爲偏似然 (partial)，就因爲它並不是一個完整的生存過程，我們只巧妙地取用了生存過程中的一部分。而且目前爲止的統計學已經證明了，它和完整的標準似然在生存數據中其實是漸進一致的 (asymptotically the same)。這也就意味着，我們可以利用這個性質，忽略掉 \(h_0(t)\)，使用極大似然法來獲取全部的 \(\beta\) 的估計值。且我們知道這些 MLE \(\hat\beta\) 的方差 (variance) 可以通過計算 Fisher information matrix 的逆矩陣 (inverse of matrix) 來獲得。這樣我們就理解了 Cox 回歸的計算原理和過程。

該偏似然的對數如果用 \(l_p\) 表示：

\[ l_p = \sum_j \beta^T x_{i_j} - \sum_j \log(\sum_{k \in R_j} \exp \beta^T x_k) \]

在最簡單的只有一個解釋變量 \(x\) 的情況之下，\(\beta\) 可以通過對該對數似然求導數之後解下列的方程獲得：

\[ \frac{dl_p}{d\beta} = \sum_j x_{i_j} - \sum_j \frac{\sum_{k \in R_j} x_k \exp \beta x_k}{\sum_{k \in R_j} \exp \beta x_k} = 0 \]

如果 \(\beta\) 是多個需要被估計的 MLE 那麼就會同時獲得多個類似上述方程的聯立方程需要同時求解。在實際操作中，統計包會選擇使用迭代法 (iterative method) 去尋找符合這樣聯立方程的解作爲 MLE。

Example 88.1 給白血病患者數據套用 Cox 比例風險回歸模型 在這個數據中，42名白血病患者中各有21人分別在治療和對照組。研究者關心的事件是病情的緩解 (remission)。追蹤時間是從白血病診斷時起，單位是週數。那麼暴露變量就是被分配到治療組與否，其中被分配到對照組的患者的風險度被認爲是基線風險度 (baseline hazard)。於是這個模型其實可以簡單描述成：

\[ \begin{cases} h_0(t) & 對照組 \text{ control group} \\ h_0(t) e^\beta & 治療組 \text{ treatment group} \end{cases} \]

使用偏似然法計算該模型的參數我們獲得對數風險度比 (log hazard ratio) 的估計值 \(\hat\beta = -1.51\)，其對應的標準誤是 \(0.410\)，95% 信賴區間是 (-2.31, -0.71)。於是相應的，風險度比 \(\exp \hat\beta = 0.22\)，95% 信賴區間是 \((0.10, 0.49)\)。

該模型用 Stata 計算的過程如下

## 
## . infile group weeks remission using https://data.princeton.edu/wws509/datasets
## > /gehan.raw
## host not found
## r(631);
## 
## . label define group 1 "control" 2 "treated"
## 
## . label values group group
## no variables defined
## r(111);
## 
## . stset weeks, failure(remission)
## variable weeks not found
## r(111);
## 
## . stcox group
## variable group not found
## r(111);
## 
## . stcox group, nohr
## variable group not found
## r(111);
## 
## .

該模型用 R 計算的過程如下

gehan <- read.table("https://data.princeton.edu/wws509/datasets/gehan.raw", 
                    header =  FALSE, sep ="", 
                    col.names = c( "group", "weeks", "remission"))

cox.model <- coxph(Surv(time = weeks, event = remission) ~ as.factor(group), 
                     data = gehan, method = "breslow")
summary(cox.model)
## Call:
## coxph(formula = Surv(time = weeks, event = remission) ~ as.factor(group), 
##     data = gehan, method = "breslow")
## 
##   n= 42, number of events= 30 
## 
##                       coef exp(coef) se(coef)       z  Pr(>|z|)    
## as.factor(group)2 -1.50919   0.22109  0.40956 -3.6849 0.0002288 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##                   exp(coef) exp(-coef) lower .95 upper .95
## as.factor(group)2   0.22109     4.5231  0.099071   0.49339
## 
## Concordance= 0.69  (se = 0.041 )
## Likelihood ratio test= 15.21  on 1 df,   p=0.0001
## Wald test            = 13.58  on 1 df,   p=0.0002
## Score (logrank) test = 15.93  on 1 df,   p=7e-05

88.3.1 爲什麼使用 Cox 回歸模型？

理由很簡單，半參數回歸模型我們放棄了對基線風險度的估計，也就是放寬了對它的限制和假設，使模型估計的結果更高效可靠 (efficient and reliable)。Cox回歸模型現在已經廣爲人知且易於理解。

Example 88.2 稍微複雜一些的例子：EPIC-Norfolk 隊列研究數據分析乳腺癌的危險因子 EPIC-Norfolk 隊列研究是一個收集了25639名觀察對象的隊列。起點觀察時間是在1990年代，全部的觀察對象都在40歲以上。該隊列研究追蹤觀察對象的多種疾病診斷和死亡，同時收集了大量的觀察對象本身的生活習慣數據，其中有飲食習慣相關數據。這個例子中我們把事件定義爲被診斷爲乳腺癌，且乳腺癌的診斷不是其他部位轉移產生的癌症，即原發乳腺癌的診斷。那麼，男性觀察對象被排除，剩下12576名女性患者作爲潛在對象集合。另外再需要排除在隨訪開始時就已經患有任意一種癌症的女性，隨訪過程中如果在未觀察到乳腺癌時就發生了其他部位的癌症的話，在診斷爲其他癌症時就被定義爲是刪失值。其餘的刪失值還包括由於非乳腺癌原因的死亡事件，或者觀察對象離開研究而致隨訪中斷。我們使用年齡作爲分析的事件尺度，圖 88.2 是該隊列的 Kaplan-Meier 生存函數曲線。

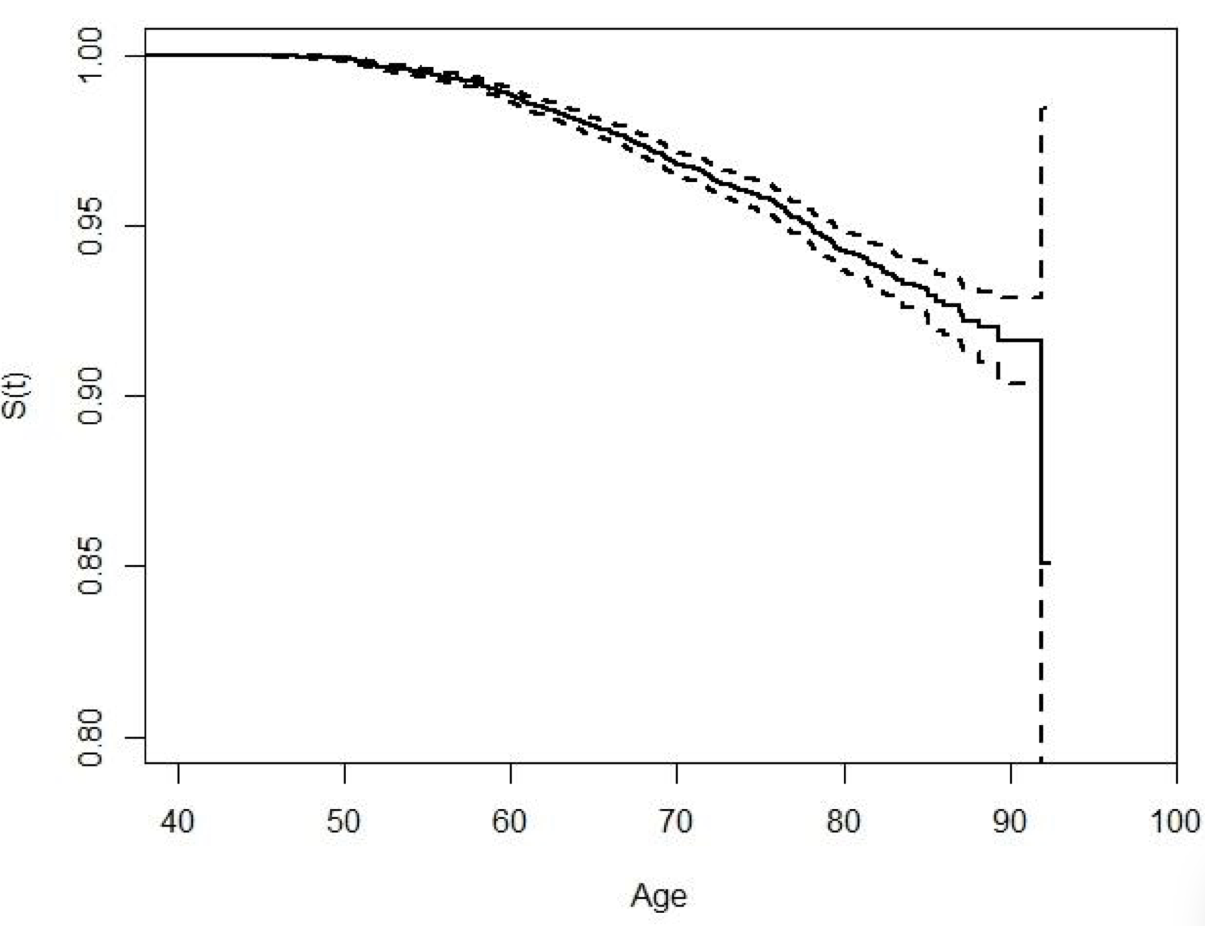
Kaplan-Meier estimate of the survival curve for women in the EPIC-Norfolk cohot (solid line), showing the 95% confidence limits (dotted lines)

圖 88.2: Kaplan-Meier estimate of the survival curve for women in the EPIC-Norfolk cohot (solid line), showing the 95% confidence limits (dotted lines)

例如我們現在的分析目的是想用該隊列收集的生活習慣分析飲酒量和被診斷爲乳腺癌的風險之間的關係。同時模型中我們還希望能夠調整其他可能的混雜因子。這裏我們先考慮兩個簡單的混雜因子，一個是家族乳癌史，還有一個是吸菸習慣。現實情況中你可能需要考慮更多的潛在混雜因子。飲酒量通過問卷調查獲得，並被換算成爲單位是每10g/天的連續型變量。家族乳癌史是二進制變量 (是/否)。吸菸習慣是三個分類的多類別變量（從未(ref)/曾經/現在吸菸）。那麼我們可以寫下這個比例風險模型的數學表達式：

\[ h(t; \mathbf{X}) = h_0(t) \exp\{ \beta_1 X_{\text{alc}} + \beta_2 X_{\text{FH}} + \beta_3 X_{\text{former-smoker}} + \beta_4 X_{\text{current-smoker}} \} \]

其中，

  • \(X_{\text{alc}}\) 是表示飲酒量的連續型變量。
  • \(X_{\text{FH}}\) 是表示是(=1)否(=0)有家族乳癌史的二進制變量。
  • \(X_{\text{former-smoker}}\) 是表示是(=1)否(=0)是曾經吸菸者的二進制變量。
  • \(X_{\text{current-smoker}}\) 是表示是(=1)否(=0)是現在吸菸者的二進制變量。

該模型的 Cox 比例風險模型分析的結果如下表：

Variable Hazard ratio 95% confidence interval p-value
\(X_{\text{alc}}\) 1.140 (1.041, 1.249) 0.005
\(X_{\text{FH}}\) 1.766 (1.337, 2.334) <0.001
\(X_{\text{former-smoker}}\) 0.875 (0.714, 1.047) 0.197
\(X_{\text{current-smoker}}\) 1.001 (0.749, 1.337) 0.995

你會解釋上面列出的風險度比的結果嗎？

88.4 處理相等的生存時間 handling tied survival times

在許多實驗和觀察研究中，生存時間會有相等的時候。也就是在某些時間點上，發生兩個及以上事件是可能的。這個可能是根據實驗對時間的定義精確度決定的。如果只是精確到週或者月，甚至是天，都有可能出現生存時間相同的情況。即使這樣，偏似然其實也是可以克服的。假如在時間點 \(t_j\) 時發生了 \(m_j\) 個事件。那麼此時，這些發生事件的對象組成的集合 \((i_{1_j}, i_{2_j}, \dots, i_{m_j})\)，如果他們的解釋變量向量是 \((x_{i_1}, x_{i_2}, \dots, x_{i_m})\) 的話，該時間點時刻發生時間的概率是

\[ \frac{h_0(t_j) \exp \beta^T x_{i_1} \times h_0(t_j) \exp \beta^T x_{i_2} \times \dots \times h_0(t_j) \exp \beta^T x_{i_m}}{\sum_{L \in R_{mj}} \prod _{l \in L} \exp \beta^T x_l} \\ = \frac{\exp(\beta^T x_{i_1} + \beta^T x_{i_2} + \dots + \beta^Tx_{i_m})}{\sum_{L \in R_{mj}}\prod _{l \in L} \exp \beta^T x_l} \]

如果數據中在相同時間點發生事件的件數較多，上面的方程變得繁瑣，因爲分母變得特別複雜。這時我們傾向於使用一個叫做 “Breslow” 估計法 (Breslow’s approximation) 來近似的計算上述方程以簡化計算：

\[ L_{p*} = \prod_j \frac{\exp(\beta^T x_{i_1} + \beta^T x_{i_2} + \dots + \beta^Tx_{i_m})}{\{ \sum_{k \in R_j} \exp \beta^T x_k \}^{m_j}} \]

R 裏的程序中也已經加入了這個近似法。

88.5 估計生存曲線

通常情況下，我們分析生存數據時只是爲了分析暴露變量和生存概率之間的關。於是基本上你看到大多數生存分析的報告和論文只是報告這些暴露變量的風險度比，及其對應的標準誤及信賴區間。那麼從我們本章目前爲止的介紹可以看出，在不需要估計基線風險 (baseline hazard) 的情況下啊，我們也可以求得我們想要的風險度比。

但是在另外一些時候，我們有期望能夠描述觀察對象中的模型估計生存概率（曲線）i.e. estimated survival curves。還有的時候，我們希望利用辛苦建立的模型來有效地預測擁有相應特徵的人羣的生存概率。例如我們在分析了白血病患者數據之後，可能希望用該數據獲得的模型來預測某些患者如果進入治療組或者放在對照組，20週以後的生存概率。這些情況下的估計和預測，就需要使用到被Cox回歸模型忽略掉的基線風險。

在全參數型模型中，如之前我們着重討論過的指數模型和 Weibull 模型，這並不是太大的問題，因爲在這些全參數模型中，基線風險也是被估計的參數之一，我們會獲得相應的基線風險估計值。怎樣在使用 Cox 回歸模型之後也能做相似的後續分析呢？

處理的思考方式是這樣的，假設某個研究對象是屬於“基線組 (baseline group)”的，那麼它/他/她身上具有的所有可能的解釋變量可以用 \(\mathbf{x}^* = (x^*_1, x^*_2, \dots, x^*_p)^T\) 表示。事實上這些變量由於是基線組，大多數可能都恰好等於零。當然也有特例，例如身高可能我們會選用平均身高作爲基線值，因爲身高爲零並不具有可比性。那麼用下面的表達式可以估計在時間點 \(t\) 時，時間段 \(t_k \leqslant t < t_{k+1}\)上的基線累積風險 (baseline cumulative hazard)：

\[ \hat H_0(t) = \sum_{j=1}^k\frac{d_j}{\sum_{l \in R_j}\exp\{ \hat\beta^T(x_l - x^*) \}} \]

其中 \(d_j\) 是在時間 \(t_j\) 時發生的事件的計數。這個方程被命名爲 “Nelson-Aalen” 估計法，或者叫 “Breslow” 估計法估計基線累積風險。從上述計算式我們可以進一步估計生存函數：

\[ \hat S(t;x) = \exp\{ - \hat H_0(t) \exp (\hat\beta^T x) \} \]

這樣就可以繪製Cox回歸模型估計的生存曲線了。

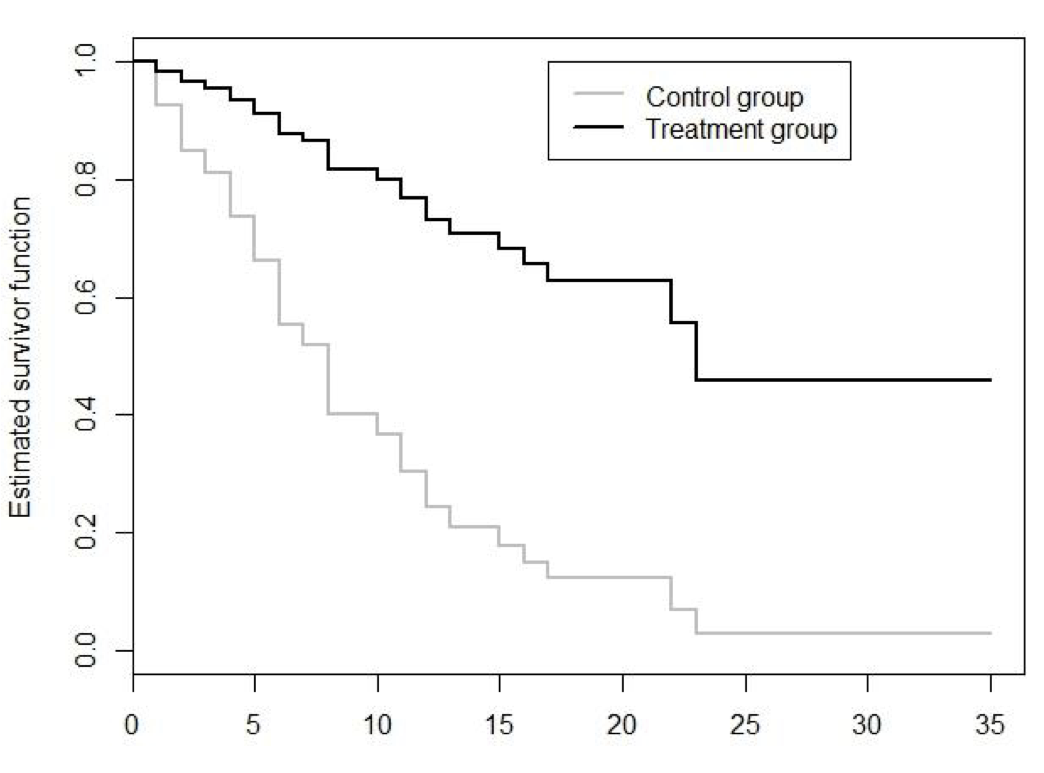
Leukaemia patients data: estimated survivor curves using the Cox proportional hazard model.

圖 88.3: Leukaemia patients data: estimated survivor curves using the Cox proportional hazard model.

Example 88.3 EPIC-Norfolk 隊列研究數據分析乳腺癌的危險因子： 之前分析過的模型中，加入了三個解釋變量 - 飲酒量（連續型），家族乳癌史（二進制型），吸菸習慣（分類型）。當你的模型類似這樣有多個模型時，不妨嘗試使用這幾個解釋變量的一些有特徵的值來繪製對應的不同組別對象的生存曲線。下圖 88.4 就是指定了四個特徵值的人的模型估計生存分析。

Breast cancer data: estimated survivor curves using the Cox proportional hazard model. [FH: family history]

圖 88.4: Breast cancer data: estimated survivor curves using the Cox proportional hazard model. [FH: family history]

88.6 Cox回歸模型中包涵的假設：

和諸多的統計模型一樣，Cox比例風險模型本身有它的前提條件。其中最顯而易見的有兩個：

\[ h(t|x) = h_0(t)e^{\beta^Tx} \]

  1. 比例風險假設 (proportional hazard assumption) - 解釋變量對與風險的作用所帶來的風險度比 (hazard ratio) 是不隨時間改變的 (hazard ratio is constant over time)。

  2. 模型構建合理假設 - 變量本身在模型中的形式是準確無誤的，特別是連續型變量。(We have correctly specified the form for how continuous explanatory variables act on the hazard);

這兩個假設本身可能互相影響，其中比例風險假設可能在連續型變量保持不變的時候不能得到滿足，也可能當你修改了連續型變量的形式的時候（例如改成二次方，或者三次方形式）得到滿足。

  1. 第三個不太明顯的假設是，刪失值是無有效生存信息的 (Uninformative censoring)。

88.7 評估比例風險假設 assessing the proportional hazard assumption

在一些簡單的情況下，如單一的二進制暴露變量。我們可以簡單的使用繪圖的方式來分析模型的比例風險假設是否得到滿足。比例風險模型下，我們有 \(h(t|x) = h_0(t)e^{\beta^Tx}\)，此時 \(x = 0 \text{ or } 1\)。用我們熟悉的生存數據函數，我們可以把它該寫成：

\[ S(t; x) = \exp\{ -\int_0^t h_0(u) e^{\beta x} du \} \]

把這個方程左右兩邊同時去對數，並轉移負號：

\[ -\log S(t;x) = e^{\beta x} \int_0^t h_0(u) du = e^{\beta x} H_0(t) \]

其中 \(H_0(t)\) 是基線累積風險函數，我們再對之同時取等式兩邊對數：

\[ \log\{ -\log S(t;x)\} = \log H_0(t) + \beta x \]

所以當 \(x\) 是二進制變量時，上面的式子等價於

\[ \log\{ -\log S(t;0)\} = \log H_0(t) \\ \log\{ -\log S(t;1)\} = \log H_0(t) + \beta \]

所以也就是說，如果比例風險假設是OK的，那麼把 \(\log\{ -\log S(t;0)\}\) 和 \(\log\{ -\log S(t;1)\} = \log H_0(t)\) 同時繪製在縱軸，橫軸是時間的話，你會看見兩條不會交叉，接近平行的曲線。此時，你可以比較有自信地認爲比例風險假設應該不太有可能被違背。特別是當你觀察到這樣兩條曲線如果產生了交叉，那可能就要重新考慮是否這個假設還能被認爲是合適的。

相似的方法你可以把它推廣到其他多分類型變量中去，區別在與多分類變量的上述曲線你會有多於兩條的最好是都互相平行的曲線，以確保假設得到滿足。

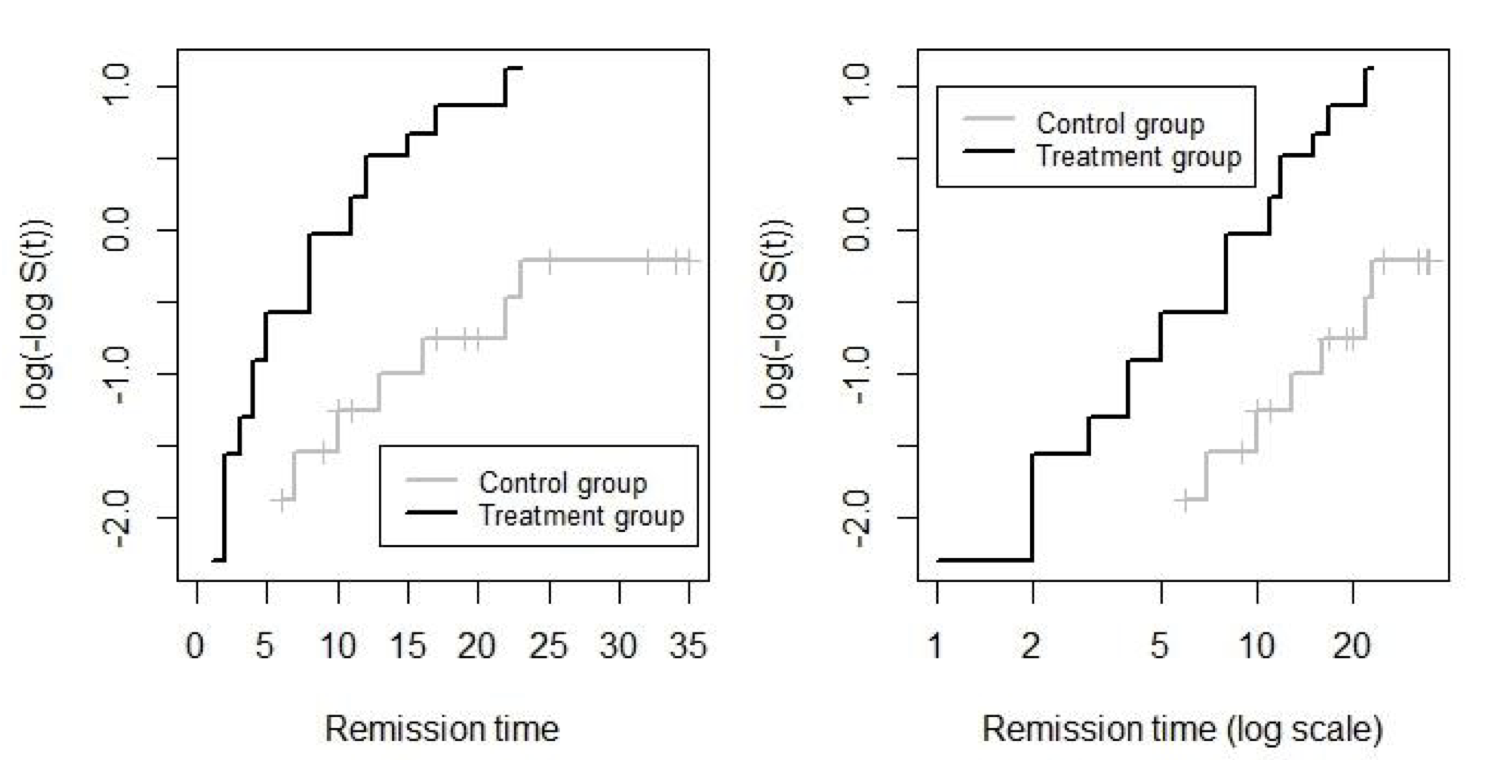
Plots of log{-logS(t;x)} against time and log time to remission among leukaemia patients in treatment and control groups

圖 88.5: Plots of log{-logS(t;x)} against time and log time to remission among leukaemia patients in treatment and control groups

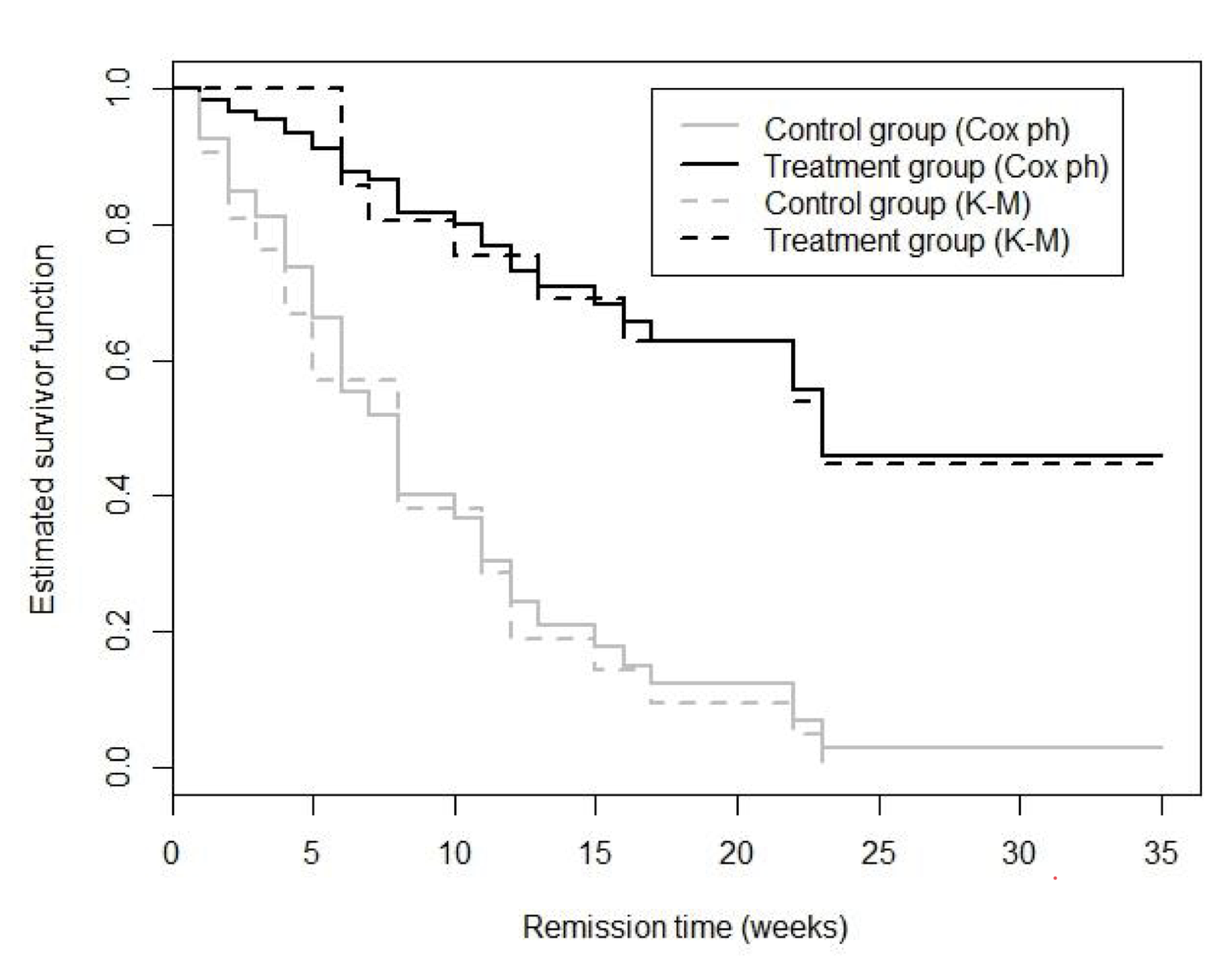
Leukaemia patient data: estimated survivor curves using the Cox proportional hazards model and using Kaplan-Meier.

圖 88.6: Leukaemia patient data: estimated survivor curves using the Cox proportional hazards model and using Kaplan-Meier.

88.8 該用半參數模型還是用全參數模型

  • 如果說指數模型或者 Weibull 模型是合理的，通常此時用 Cox 半參數模型也是合理的；
  • 如果指數模型或者 Weibull 模型都是合理的，那麼 Cox 半參數模型給出的估計，其實不會和指數模型或者 Weibull 模型相差甚遠。指數模型或者 Weibull 模型可能給出的估計會相對更精確 (更小的標準誤)，但是實際應用中這種更加精確的程度其實十分有限；
  • 另外，使用指數模型或者 Weibull 模型，重要的基線風險是否被模型擬合正確將會是關鍵 (baseline hazard mis-specified?)，但是使用 Cox 模型，就可以避免這個假設，忽略掉基線風險；
  • 2002 年，(Royston and Parmar 2002) 提出第三種生存數據模型，“flexible parametric survival models”，結合了參數和半參數模型的長處，正在變得流行起來。在這個新型靈活參數生存模型中，使用了三次方程平滑曲線 (cubic splines modelled smoothly) 擬合對數基線累積風險 (log cumulative baseline hazard)。

88.9 Practical Survival 04

##########################################################
##########################pbc data########################
##########################################################
library(survival)
library(haven)
pbc <- read_dta("../backupfiles/pbcbase.dta")


##question 1##

pbc.cox1<-coxph(Surv(time,d) ~ as.factor(treat),data=pbc)
summary(pbc.cox1)
## Call:
## coxph(formula = Surv(time, d) ~ as.factor(treat), data = pbc)
## 
##   n= 191, number of events= 96 
## 
##                       coef exp(coef) se(coef)       z Pr(>|z|)
## as.factor(treat)2 -0.15501   0.85640  0.20556 -0.7541   0.4508
## 
##                   exp(coef) exp(-coef) lower .95 upper .95
## as.factor(treat)2    0.8564     1.1677   0.57241    1.2813
## 
## Concordance= 0.503  (se = 0.028 )
## Likelihood ratio test= 0.57  on 1 df,   p=0.5
## Wald test            = 0.57  on 1 df,   p=0.5
## Score (logrank) test = 0.57  on 1 df,   p=0.5
pbc.cox2<-coxph(Surv(time,d)~bil0,data=pbc)
summary(pbc.cox2)
## Call:
## coxph(formula = Surv(time, d) ~ bil0, data = pbc)
## 
##   n= 191, number of events= 96 
## 
##           coef exp(coef)  se(coef)      z  Pr(>|z|)    
## bil0 0.0067119 1.0067345 0.0007971 8.4203 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##      exp(coef) exp(-coef) lower .95 upper .95
## bil0    1.0067    0.99331    1.0052    1.0083
## 
## Concordance= 0.777  (se = 0.023 )
## Likelihood ratio test= 43.38  on 1 df,   p=5e-11
## Wald test            = 70.9  on 1 df,   p=<2e-16
## Score (logrank) test = 93.31  on 1 df,   p=<2e-16
##question 2##

pbc.1<-survfit(Surv(time,d)~as.factor(treat),data=pbc)

plot(pbc.1,mark.time=F,
col=c("blue","red"),fun="cloglog",xlab="time (log scale)",ylab="log(-log S(t))")
legend(0.02,0,c("Treat=1","Treat=2"),col=c("blue","red"),lty=1)

pbc$bil_q<-cut(pbc$bil0,breaks=quantile(pbc$bil0,probs=seq(0,1,0.25)))

pbc.2<-survfit(Surv(time,d)~as.factor(bil_q),data=pbc)

plot(pbc.2,mark.time=F,
col=c("blue","red","green","yellow"),fun="cloglog",xlab="time (log scale)",ylab="log(-log S(t))")
legend(0.02,0,c("bil0: group 1","bil0: group 2","bil0: group 3","bil0: group 4"),col=c("blue","red","green","yellow"),lty=1)

pbc.cox<-coxph(Surv(time,d)~treat,data=pbc)

plot(survfit(pbc.cox,newdata=data.frame(treat=c(0,1))),mark.time=F,col=c("grey","black"),xlab="Time",ylab="Estimated survivor function")

pbc.km<-survfit(Surv(time,d)~as.factor(treat),data=pbc)

lines(pbc.km,mark.time=F,col=c("grey","black"),lty=2,add=T)

legend(8,1,c("Treat=1, Cox","Treat=2, Cox","Treat=1, Kaplan-Meier","Treat=2, Kaplan-Meier"),col=c("grey","black","grey","black"),lty=c(1,1,2,2))

#question 3

pbc.cox<-coxph(Surv(time,d)~treat+bil0,data=pbc)
summary(pbc.cox)
## Call:
## coxph(formula = Surv(time, d) ~ treat + bil0, data = pbc)
## 
##   n= 191, number of events= 96 
## 
##              coef   exp(coef)    se(coef)       z Pr(>|z|)    
## treat -0.38381178  0.68125964  0.21425185 -1.7914  0.07323 .  
## bil0   0.00711080  1.00713614  0.00083482  8.5177  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##       exp(coef) exp(-coef) lower .95 upper .95
## treat   0.68126    1.46787   0.44765    1.0368
## bil0    1.00714    0.99291   1.00549    1.0088
## 
## Concordance= 0.746  (se = 0.026 )
## Likelihood ratio test= 46.6  on 2 df,   p=8e-11
## Wald test            = 72.98  on 2 df,   p=<2e-16
## Score (logrank) test = 96.22  on 2 df,   p=<2e-16
pbc.km.bil0.1<-survfit(Surv(time,d)~as.factor(bil_q),data=subset(pbc,treat==1))
pbc.km.bil0.2<-survfit(Surv(time,d)~as.factor(bil_q),data=subset(pbc,treat==2))

par(mfrow=c(1,2))

plot(pbc.km.bil0.1,mark.time=F,col=c("blue","red","green","yellow"),fun="cloglog",xlab="time (log scale)",ylab="log(-log S(t))",main="Treatment group 1")
legend(0.02,1,c("bil0: group 1","bil0: group 2","bil0: group 3","bil0: group 4"),col=c("blue","red","green","yellow"),lty=1)

plot(pbc.km.bil0.2,mark.time=F,col=c("blue","red","green","yellow"),fun="cloglog",xlab="time (log scale)",ylab="log(-log S(t))",main="Treatment group 2")
legend(0.02,1,c("bil0: group 1","bil0: group 2","bil0: group 3","bil0: group 4"),col=c("blue","red","green","yellow"),lty=1)

#question 4

pbc.cox.sq<-coxph(Surv(time,d)~treat+bil0+I(bil0^2),data=pbc)
summary(pbc.cox.sq)
## Call:
## coxph(formula = Surv(time, d) ~ treat + bil0 + I(bil0^2), data = pbc)
## 
##   n= 191, number of events= 96 
## 
##                   coef    exp(coef)     se(coef)       z  Pr(>|z|)    
## treat     -0.406076880  0.666258943  0.211007470 -1.9245    0.0543 .  
## bil0       0.021833018  1.022073102  0.003126447  6.9833 2.883e-12 ***
## I(bil0^2) -0.000033812  0.999966188  0.000008092 -4.1785 2.935e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##           exp(coef) exp(-coef) lower .95 upper .95
## treat       0.66626     1.5009   0.44059   1.00752
## bil0        1.02207     0.9784   1.01583   1.02836
## I(bil0^2)   0.99997     1.0000   0.99995   0.99998
## 
## Concordance= 0.769  (se = 0.024 )
## Likelihood ratio test= 74.21  on 3 df,   p=5e-16
## Wald test            = 86.87  on 3 df,   p=<2e-16
## Score (logrank) test = 109.58  on 3 df,   p=<2e-16
exp(pbc.cox.sq$coef[1]+60*pbc.cox.sq$coef[2]+(60^2)*pbc.cox.sq$coef[3])/exp(50*pbc.cox.sq$coef[2]+(50^2)*pbc.cox.sq$coef[3])
##      treat 
## 0.79856415
#question 5
pbc.cox.sq<-coxph(Surv(time,d)~treat+bil0+I(bil0^2),data=pbc)

par(mfrow=c(1,1))

plot(survfit(pbc.cox.sq,newdata=data.frame(treat=c(0,1),bil0=50)),mark.time=F,col=c("grey","black"),xlab="Time",ylab="Estimated survivor function")
legend(7,1,c("Treatment group 1","Treatment group 2"),col=c("grey","black"),lty=1)

##########################################################
##########################whitehall#######################
##########################################################
whl <- read.table("../backupfiles/whitehall.csv",sep=",",header=T)

whl$agecat<-cut(whl$agein, breaks=c(40,50,55,60,65,70),right=F,labels=F)

my.mod1<-coxph(Surv(time=timein,time2=timeout,event=chd,origin=timein)~grade,data=whl)
summary(my.mod1)
## Call:
## coxph(formula = Surv(time = timein, time2 = timeout, event = chd, 
##     origin = timein) ~ grade, data = whl)
## 
##   n= 1677, number of events= 154 
## 
##          coef exp(coef) se(coef)     z   Pr(>|z|)    
## grade 0.71396   2.04207  0.16368 4.362 0.00001289 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##       exp(coef) exp(-coef) lower .95 upper .95
## grade    2.0421     0.4897    1.4817    2.8145
## 
## Concordance= 0.585  (se = 0.02 )
## Likelihood ratio test= 17.94  on 1 df,   p=2e-05
## Wald test            = 19.03  on 1 df,   p=1e-05
## Score (logrank) test = 19.85  on 1 df,   p=8e-06
my.mod2<-coxph(Surv(time=timein,time2=timeout,event=chd,origin=timein)~grade+as.factor(agecat),data=whl)
summary(my.mod2)
## Call:
## coxph(formula = Surv(time = timein, time2 = timeout, event = chd, 
##     origin = timein) ~ grade + as.factor(agecat), data = whl)
## 
##   n= 1677, number of events= 154 
## 
##                        coef exp(coef) se(coef)      z  Pr(>|z|)    
## grade               0.28128   1.32483  0.17555 1.6022 0.1091028    
## as.factor(agecat)2  0.97495   2.65104  0.25820 3.7759 0.0001594 ***
## as.factor(agecat)3  1.48454   4.41294  0.24190 6.1370 8.409e-10 ***
## as.factor(agecat)4  1.53513   4.64193  0.27109 5.6627 1.490e-08 ***
## as.factor(agecat)5  2.57802  13.17110  0.37706 6.8372 8.077e-12 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##                    exp(coef) exp(-coef) lower .95 upper .95
## grade                 1.3248   0.754816   0.93913    1.8689
## as.factor(agecat)2    2.6510   0.377210   1.59821    4.3974
## as.factor(agecat)3    4.4129   0.226606   2.74677    7.0898
## as.factor(agecat)4    4.6419   0.215428   2.72862    7.8968
## as.factor(agecat)5   13.1711   0.075924   6.29025   27.5788
## 
## Concordance= 0.706  (se = 0.019 )
## Likelihood ratio test= 84.15  on 5 df,   p=<2e-16
## Wald test            = 80.17  on 5 df,   p=8e-16
## Score (logrank) test = 103.3  on 5 df,   p=<2e-16
#We can do the same thing as follows (note the change in the Surv function)

my.mod1<-coxph(Surv(time=(timeout-timein),event=chd)~grade,data=whl)
summary(my.mod1)
## Call:
## coxph(formula = Surv(time = (timeout - timein), event = chd) ~ 
##     grade, data = whl)
## 
##   n= 1677, number of events= 154 
## 
##          coef exp(coef) se(coef)     z   Pr(>|z|)    
## grade 0.71396   2.04207  0.16368 4.362 0.00001289 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##       exp(coef) exp(-coef) lower .95 upper .95
## grade    2.0421     0.4897    1.4817    2.8145
## 
## Concordance= 0.585  (se = 0.02 )
## Likelihood ratio test= 17.94  on 1 df,   p=2e-05
## Wald test            = 19.03  on 1 df,   p=1e-05
## Score (logrank) test = 19.85  on 1 df,   p=8e-06
my.mod2<-coxph(Surv(time=(timeout-timein),event=chd)~grade+as.factor(agecat),data=whl)
summary(my.mod2)
## Call:
## coxph(formula = Surv(time = (timeout - timein), event = chd) ~ 
##     grade + as.factor(agecat), data = whl)
## 
##   n= 1677, number of events= 154 
## 
##                        coef exp(coef) se(coef)      z  Pr(>|z|)    
## grade               0.28128   1.32483  0.17555 1.6022 0.1091028    
## as.factor(agecat)2  0.97495   2.65104  0.25820 3.7759 0.0001594 ***
## as.factor(agecat)3  1.48454   4.41294  0.24190 6.1370 8.409e-10 ***
## as.factor(agecat)4  1.53513   4.64193  0.27109 5.6627 1.490e-08 ***
## as.factor(agecat)5  2.57802  13.17110  0.37706 6.8372 8.077e-12 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##                    exp(coef) exp(-coef) lower .95 upper .95
## grade                 1.3248   0.754816   0.93913    1.8689
## as.factor(agecat)2    2.6510   0.377210   1.59821    4.3974
## as.factor(agecat)3    4.4129   0.226606   2.74677    7.0898
## as.factor(agecat)4    4.6419   0.215428   2.72862    7.8968
## as.factor(agecat)5   13.1711   0.075924   6.29025   27.5788
## 
## Concordance= 0.706  (se = 0.019 )
## Likelihood ratio test= 84.15  on 5 df,   p=<2e-16
## Wald test            = 80.17  on 5 df,   p=8e-16
## Score (logrank) test = 103.3  on 5 df,   p=<2e-16
#using age as the time scale with delayed entry 

my.mod3<-coxph(Surv(time=timein,time2=timeout,event=chd,origin=timebth)~grade,data=whl)
summary(my.mod3)
## Call:
## coxph(formula = Surv(time = timein, time2 = timeout, event = chd, 
##     origin = timebth) ~ grade, data = whl)
## 
##   n= 1677, number of events= 154 
## 
##          coef exp(coef) se(coef)      z Pr(>|z|)  
## grade 0.34027   1.40533  0.16794 2.0262  0.04274 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##       exp(coef) exp(-coef) lower .95 upper .95
## grade    1.4053    0.71158    1.0112    1.9531
## 
## Concordance= 0.555  (se = 0.022 )
## Likelihood ratio test= 4.02  on 1 df,   p=0.05
## Wald test            = 4.11  on 1 df,   p=0.04
## Score (logrank) test = 4.14  on 1 df,   p=0.04
my.mod4<-coxph(Surv(time=timein,time2=timeout,event=chd,origin=timebth)~grade+as.factor(agecat),data=whl)
summary(my.mod4)
## Call:
## coxph(formula = Surv(time = timein, time2 = timeout, event = chd, 
##     origin = timebth) ~ grade + as.factor(agecat), data = whl)
## 
##   n= 1677, number of events= 154 
## 
##                       coef exp(coef) se(coef)      z Pr(>|z|)  
## grade              0.26575   1.30441  0.17541 1.5150  0.12976  
## as.factor(agecat)2 0.32814   1.38839  0.28010 1.1715  0.24140  
## as.factor(agecat)3 0.54328   1.72165  0.29050 1.8701  0.06146 .
## as.factor(agecat)4 0.31074   1.36444  0.33982 0.9144  0.36049  
## as.factor(agecat)5 1.14826   3.15269  0.44609 2.5741  0.01005 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##                    exp(coef) exp(-coef) lower .95 upper .95
## grade                 1.3044    0.76663   0.92493    1.8396
## as.factor(agecat)2    1.3884    0.72026   0.80184    2.4040
## as.factor(agecat)3    1.7217    0.58084   0.97425    3.0424
## as.factor(agecat)4    1.3644    0.73290   0.70096    2.6559
## as.factor(agecat)5    3.1527    0.31719   1.31513    7.5578
## 
## Concordance= 0.58  (se = 0.026 )
## Likelihood ratio test= 12.07  on 5 df,   p=0.03
## Wald test            = 13.08  on 5 df,   p=0.02
## Score (logrank) test = 13.56  on 5 df,   p=0.02

References

Cox, David R. 1972. “Models and Life-Tables Regression.” JR Stat. Soc. Ser. B 34: 187–220.
Royston, Patrick, and Mahesh KB Parmar. 2002. “Flexible Parametric Proportional-Hazards and Proportional-Odds Models for Censored Survival Data, with Application to Prognostic Modelling and Estimation of Treatment Effects.” Statistics in Medicine 21 (15): 2175–97.