第 91 章 生存分析的其他手段
91.1 分層Cox生存分析 stratified Cox proportional hazards model
Under the Cox proportional hazards model, the effect of each explanatory variable on the hazard is assumed to be such that the ratio of hazards is constant accross the time scale (the proportional hazards assumption). In applications with several explanatory variabls, the effect of some of these variables may not be proportional. When the aim of the analysis is not focussed on these particular variables, for example if they are just being used as adjustment variables and are not the main exposures of interest, then the proportionality assumption can be relaxed just for those variables by fitting a stratified Cox proportional hazards model.
In the stratified Cox proportional hazards model, instead of assuming that the proportional hazards model holds overall, we assume that the proportional hazards assumption holds within groups (or strata) of individuals.
\[ h(t|x,s) = h_{0s} (t)e^{\beta^T x} \]
Each stratum, s, has a separate baseline hazard \(h_{0s}(t)\). However, the other explanatory variables x are assumed to act in the same way on the baseline hazard in each stratum, i.e. the \(\beta\) are the same accross strata.
91.2 加速失效(死亡)模型 Accelerated failure time (AFT) model
加速失效模型,AFT 模型的特點是不管所謂的風險概念,而是對每個患者真正的生存時間進行模型化處理,其實個人更加喜歡這個模型,因為它很直觀地告訴你某類人的生存時間就是比另一類人短,而不是告訴你一個抽象的一組的風險低於或者高於另一組,因為很多人無法理解什麼是風險 (hazard),正如很多人無法理解什麼是比值 (odds) 一樣。同樣還因為風險比例模型還要考慮是否對基線風險進行參數估計的取捨問題。
所以,我們先來回憶一下風險比例模型的定義。當解釋變量 (explanatory variable) 是一個二分類型變量,例如治療組和對照組。我們用 \(h_0(t)\) 表示在時間點 \(t\) 時,對照組 (control or baseline group) 的風險度方程 (hazard function)。那麼當比例風險成立時 (proportional hazard),治療組的風險度方程和對照組的風險度方程成比例,如下面的式子所示:
\[ h_1(t) = \psi_{PH}h_0(t) \]
在比例風險模型中,我們需要進行估計的(to be estimated),就是上面式子中的比例係數 \(\psi_{PH}\)。另外,基線風險度,baseline hazard \(h_0(t)\),也是可參數化的 (can be parameterized)。例如我們認爲生存數據服從指數分佈 (exponential distribution, see Chapter 85.8.1) 時,對照組的風險度被認爲不隨着時間而變化,是恆定的 (\(h_0(t) = \lambda\))。如果我們認爲對照組風險度其實是會隨着時間而單調遞增或者單調遞減時,那麼它服從 Weibull 分佈 (see Chapter 85.8.2) 基線的風險度就是 \(h_0(t) = \kappa \lambda t^{\kappa -1}\)。在一般常用的 Cox 比例風險模型中,這個基風險度被忽略而不進行參數化。
其實有時候我們可以簡單一點地思考這個生存數據,讓我們換一個角度看待我們的研究問題到底問的是什麼。發自我們內心的,其實,如果你也承認,我們會更加關心的是治療組,相比對照組的患者,生存時間 (survival time)上有沒有差異,而不是抽象的(難以理解的)風險度 (hazard) 的差異。
所以,我們這一章節想要討論的加速失效(死亡)模型,簡稱 AFT 模型就是用於比較組與組之間生存時間 \((T)\) 差異的模型。假設 \(T_0\) 是對照組(基線組 baseline group)的生存時間,那麼 \(T_1\) 表示治療組的生存時間,假如治療本身對生存時間的影響可以使用乘法的方式來表達,那麼治療組和對照組之間生存時間的關係可以描述成:
\[ T_1 = \psi_{AFT}T_0 \]
在 AFT 模型中,\(\psi_{AFT}\) 就是加速指數,它的直接涵義就是,治療組患者的死亡時間被“加速”或者“減緩”了。也就是它可以回答,治療組的患者是不是更快的痊癒?或者更快的死亡?這樣明了的問題。假設我們估計說,\(\psi_{AFT} = 2\),這就可以被解釋成是,治療組患者的生存時間,是對照組患者生存時間的兩倍,也就是說,治療使得患者發生死亡的時間被推遲了。
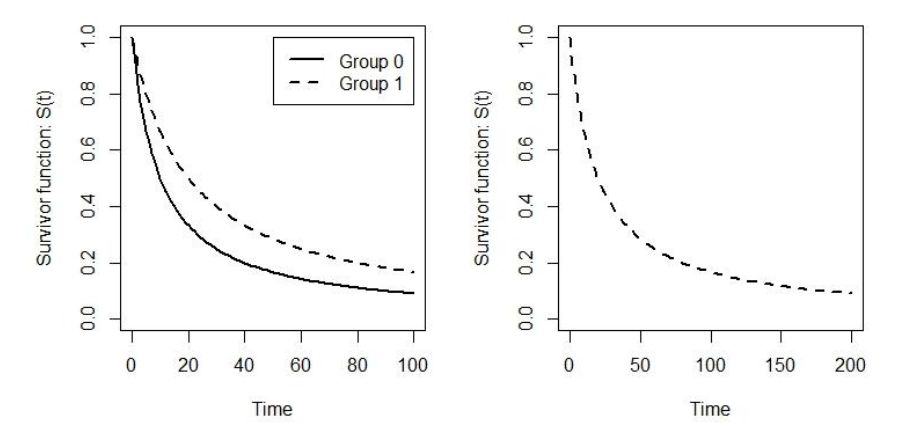
圖 91.1: The survival curve in the treatment and control groups when accelerated factor = 2 (left); and the survivor curve for the treatment group again (right), but with the scale of the time axis changed.
91.2.1 詳細推導
繼續一邊和比例風險模型對比一邊推導加速失效模型。在比例風險模型中 \(h_1(t) = \psi_{PH}h_0(t)\),我們常常用 \(e^{\beta_{PH}}\) 取代 \(\psi_{PH}\)。這樣一來,就可以避免估計風險比例係數時只能是正數這樣的取值範圍限制,也就是指數函數中的 \(\beta_{PH}\) 現在就又可以取所有實數啦,可正,可負。所以我們也可以用類似的思維對加速失效模型的加速度參數進行參數化分析,通常情況下,這個加速度指數用 \(e^{-\beta_{AFT}}\) 進行參數化分析,稍後的解釋可以讓我們更加理解這裏爲什麼被加上了一個減號:
\[ T_1 = T_0 e^{-\beta_{AFT}} \]
在AFT模型中,用生存方程會更加直觀。對照組(基線組)的生存方程用 \(S_0(t)\) 表示的話,那麼治療組的生存方程 \(S_1(t)\) 可以表示爲:
\[ \begin{aligned} S_1(t) & = \text{Pr}(T_1 > t) \\ & = \text{Pr}(e^{-\beta_{AFT}}T_0 > t) \\ & = \text{Pr}(T_0 > te^{\beta_{AFT}}) \\ & = S_0(e^{\beta_{AFT}}t) \end{aligned} \]
也就是說,治療組的生存方程和對照組是相同的,只是時間 \(t\) 被替換成了 \(e^{\beta_{AFT}}t\)。這樣一來,治療組,對照組患者的生存方程的分佈形狀 (shape of survival distribution),其實是相同的,但是兩組之間的時間軸在前進的速度上有差異(更快了,或者更慢了)。也就是說,治療組相比較對照組,在走到同一個終點(死亡)之前的時間過程中,被按了快進鍵(或者減速鍵)。所以如果 \(e^{\beta_{AFT}} > 1\),那麼治療組的患者發生(死亡)事件之前的時間較短,所以治療加速了死亡進程。如果 \(e^{\beta_{AFT}} < 1\),那麼治療組患者發生(死亡)事件之前的時間較長,所以治療延長了死亡進程。所以你會看見,這個 \(e^{\beta_{AFT}}\) 沒有類似風險度比 (hazard ratio) 那樣的意義,它是一個加速度指數。人最終都是會走向死亡的,只是時間長短的問題。
91.2.2 再詳細推導
目前爲止,我們只討論了當解釋變量是一個而分類變量時的情況。更加一般性地,當我們有一串觀察變量組成的向量 (a vector of explanatory variables) \(\mathbf{x}\),在AFT模型下它的生存方程可以描述成:
\[ S(t;\mathbf{x}) = S_0(te^{\beta_{AFT}^T\mathbf{x}}) \]
上述模型中,\(S_0\) 是基線組個體的生存方程,其中 \(\beta_{AFT}\) 則變成了各解釋變量的回歸係數構成的向量 (a vector of parameters)。
那麼,很容易地,我們可以寫下一般情況下,AFT模型中的風險度方程 (hazard function, \(h(t;\mathbf{x})\)),和生存概率密度方程 (probability density function, \(f(t;\mathbf{x})\)):
\[ \begin{aligned} h(t;\mathbf{x}) & = h_0(te^{\beta_{AFT}^T\mathbf{x}})e^{\beta_{AFT}^T\mathbf{x}} \\ f(t;\mathbf{x}) & = f_0(te^{\beta_{AFT}^T\mathbf{x}})e^{\beta_{AFT}^T\mathbf{x}} \end{aligned} \]
91.2.3 風險比例模型(PH)和加速失效(死亡)模型(AFT)的比較
詳細比較兩種模型下,風險度方程和生存方程表達的不同。這裏我們繼續用簡單的二分類變量(治療組,對照組)來簡化數學模型:
| 模型 | 風險度方程 (hazard function) | 生存方程 (survivor function) |
|---|---|---|
| PH | 對照組: \(h_0(t)\) | 對照組: \(S_0(t) = \exp\{-\int_0^th_0(u) du\}\) |
| 治療組: \(h_1(t) = e^{\beta_{PH}}h_0(t)\) | 治療組: \(S_1(t) = S_0(t)^{\exp(\beta_{PH})} = \exp\{ -e^{\beta_{PH}}\int_0^th_0(u) du \}\) | |
| AFT | 對照組: \(h_0(t)\) | 對照組: \(S_0(t) = \exp\{-\int_0^th_0(u) du\}\) |
| 治療組: \(h_1(t) = e^{\beta_{AFT}} h_0( e^{\beta_{AFT}} t)\) | 治療組: \(S_1(t) = S_0(e^{\beta_{AFT}}t) = \exp\{-e^{\beta_{AFT}}\int_0^th_0(e^{\beta_{AFT}}u)du\}\) |
91.2.4 Weibull 模型也是一種 AFT 模型
上述的討論,是對AFT模型的一般化的討論。但是和風險比例模型相似的,AFT模型其實也是一大類的生存分析模型 (a family of models)。這裏我們討論一下 Weibull 模型的另一種表達方式。
Weibull 模型下,對照組的生存方程 (survival function, \(S_0(t)\)) 被描述爲:
\[ S_0(t) = \exp\{-\lambda t^{\kappa}\} \]
那麼,治療組的生存方程 (\(S_1(t)\)) 可以被描述爲:
\[ S(t;\mathbf{x}) = \exp\{-\lambda(te^{\beta_{AFT}^T\mathbf{x}})^\kappa\}= \exp\{-\lambda e^{\kappa \beta_{AFT}^T\mathbf{x}} t^\kappa\} \]
你如果仔細觀察,認真思考,就不難發現,其實這個治療組的生存方程,也是服從Weibull分佈的方程,只是和對照組生存方程相比,\(\lambda\) 被替換成了 \(\lambda e^{\kappa \beta_{AFT}^T\mathbf{x}}\)。也就是說,不論是對照組還是治療組,患者的生存時間都服從Weibull分佈,差別只在於某些解釋變量 (explanatory variables) 改變了 Weibull 分佈的某些參數。所以我們說,Weibull分佈,也是一種特殊形態的AFT模型。
但是,我們之前探討 Weibull 模型時,只討論了它在風險比例前提下的形式:
\[ S(t;\mathbf{x}) = \exp\{-\lambda e^{\beta^T_{PH}\mathbf{x}} t^\kappa \} \]
一個 Weibull 模型在 AFT 模型下的生存方程是:
\[ S(t;\mathbf{x}) = \exp \{ -\lambda e^{\kappa \beta^T_{AFT}\mathbf{x}} t^\kappa \} \]
所以當你用 Weibull 模型時,其實可以自由在兩種類型 (PH or AFT) 之間自由切換:
\[ \exp(\beta^T_{PH}) = \exp(\kappa\beta^T_{AFT}) \]
Weibull 模型和其特殊形態–指數模型,為唯二的兩個,可以在 PH 模型和 AFT 模型之間自由切換的模型。