第 17 章 正態誤差模型 Normal error models
正態誤差模型,其實沒有其名字那麼複雜,就是討論在正態分布條件下,均值和方差都需要被估計 (都是未知狀態) 的模型。
本章還介紹
- \(F\) 分佈和 \(t\) 分佈,試着闡述如何將 \(t\) 分佈應用於兩個獨立樣本均值的比較;
- \(\chi^2\) 分佈在統計學中各種常用分佈中的中心位置。
17.1 服從正態分佈的隨機變量
\[ X_1,\cdots,X_n \stackrel{i.i.d}{\sim} N(\mu,\sigma^2) \Leftrightarrow \bar{X} \sim N(\mu, \frac{\sigma^2}{n}) \]
如果總體方差 \(\sigma^2\) 已知 (理想狀態,現實中不太可能):
\[ \begin{aligned} & Z=\frac{\bar{X}-\mu}{\sigma/\sqrt{n}} \sim N(0,1) \\ & 95\% \text{CI for } \mu = \bar{X} \pm Z_{0.975}\frac{\sigma}{\sqrt{n}} \\ & \text{H}_0: \mu=\mu_0 \Rightarrow \frac{\bar{X}-\mu_0}{\sigma/\sqrt{n}} \sim N(0,1) \end{aligned} \]
如果總體方差 \(\sigma^2\) 是未知的,腫麼辦? (模型中出現了兩個參數 \(\mu \;\&\; \sigma^2\))
\[ T=\frac{\bar{X}-\mu_0}{\hat\sigma/\sqrt{n}} \sim ????????? \]
17.2 \(F\) 分佈和 \(t\) 分佈的概念
如果 \(X\sim N(0,1)\),那麼 \(X^2 \sim \chi^2_1\) (Section 11)。類似地,如果 \(X_1,\cdots,X_n \stackrel{i.i.d}{\sim} N(0,1)\) 那麼 \(\sum_{i=1}^n X^2_i \sim \chi^2_k\)。
\(F\) 分佈和 \(t\) 分佈是建立在 \(\chi^2\) 分佈的基礎上的:
- \(F\) 分佈: \(Y_1, Y_2\) 是獨立的兩個隨機變量,且 \(Y_1 \sim \chi^2_{k_1}; Y_2 \sim \chi^2_{k_2}\),那麼
\[ F=\frac{Y_1/k_1}{Y_2/k_2} \sim F_{k_1, k_2} \]
- \(t\) 分佈,是 \(F\) 分佈的特殊情況 \((k_1=1)\):
\[ T\sim t_{k_2} \Rightarrow T^2 = \frac{Y_1/1}{Y_2/k_2} \sim F_{1,k_2} \]
此時我們再來考慮正態分佈模型中有兩個參數 \(\mu, \sigma^2\) 需要被估計的模型:
\[ Y_i \stackrel{i.i.d}{\sim} N(\mu,\sigma^2) \text{ where } i = 1, \cdots, n \]
其實可以改寫爲
\[ \begin{aligned} & Y_i = \mu + \varepsilon_i \\ & \text{Where } \varepsilon_i \stackrel{i.i.d}{\sim} N(0,\sigma^2) \end{aligned} \]
其中 \(\varepsilon_i \stackrel{i.i.d}{\sim} N(0,\sigma^2)\) 就是正態誤差 normal (random) error。\(Y_i = \mu + \varepsilon_i\) 就是正態誤差模型 normal error model。誤差的含義就是統計模型中的隨機誤差 (模型不能解釋的部分)。如果一個正態誤差模型像前面的式子這樣沒有其他變量,那麼所有的觀察值 \(Y_i\),就是由總體均值 \(\mu\) population mean,和隨機誤差 \(\varepsilon\) random error 來說明 (就是這個式子 \(Y_i = \mu + \varepsilon_i\))。
如果觀察值 \(Y_i\) 的一部分除了可以用均值解釋,還可以由某個變量 \(x\) 來說明 (叫做解釋變量 explanatory variable 詳見線性迴歸部分 Section 27.3.3),即:
\[ \begin{aligned} &Y_i | x \stackrel{i.i.d}{\sim} N(\mu+\beta x_i, \sigma^2)\\ & E(Y|x) = \mu+\beta x, \text{Var}(Y|x) = \sigma^2 \\ & \text{ or } Y_i|x = \mu + \beta x_i + \varepsilon_i ; \text{ where } \varepsilon_i \stackrel{i.i.d}{\sim} N(0, \sigma^2) \end{aligned} \]
上面的模型會在後面講線性迴歸的部分深入探討,此處簡單用下面的圖形來輔助理解。圖 17.1 中繪製的是 \(Y_i|x = \mu + \beta x_i + \varepsilon_i ; \text{ where } \varepsilon_i \stackrel{i.i.d}{\sim} N(0, \sigma^2)\) 的示意圖,用 \(x_i\) 標記兩個組,其中 \(x_i = 0\) 時爲組 A 的人的觀察值,\(x_i=1\) 時爲組 B 的人的觀察值。兩組的平均值如 Y 軸顯示的那樣,組 A 是 \(\mu\),組 B 是 \(\mu+\beta\)。所以,這裏可以看到,正態誤差模型是假定兩組具有相同的方差的 common variance,如圖 17.2。如果解釋變量 (explanatory variable) 是一個連續型變量,則解釋爲在 X 軸上的任意一點對應的 Y 值的誤差都服從相同的方差,如圖 17.3
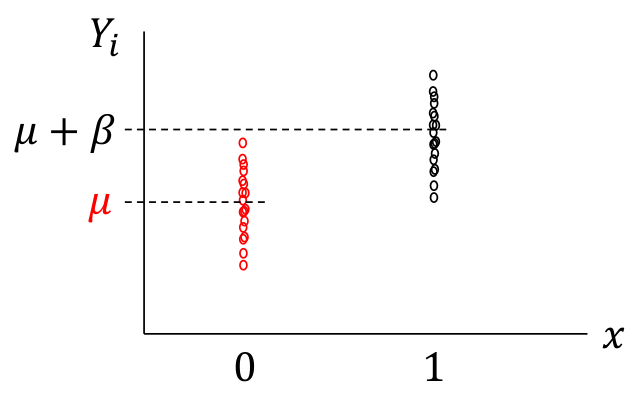
圖 17.1: Normal error models with categorical explanatory variable
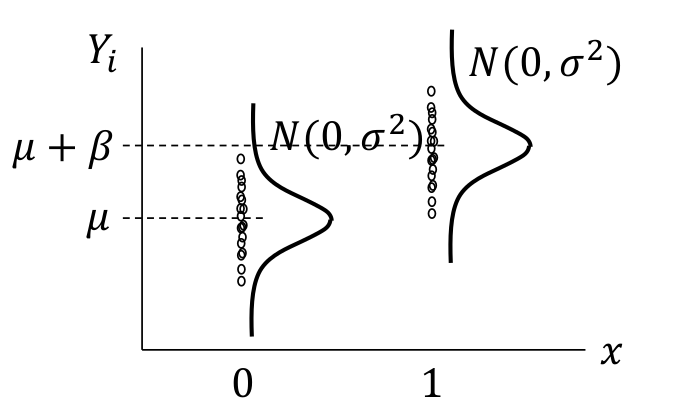
圖 17.2: Normal error models shown with common error variance
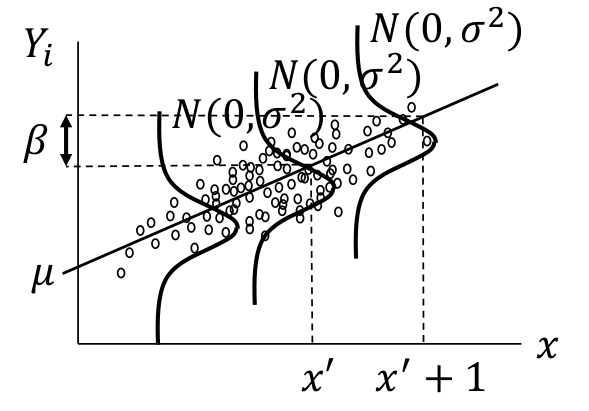
圖 17.3: Normal error models shown with continuous variable and common error variance
17.3 兩個參數的模型
17.3.1 一組數據兩個參數
如果觀察數據 \(\underline{x} = x_1, \cdots, x_n\) 是互相獨立的,該觀察數據的模型可以用一個包含兩個參數 \(\theta,\phi\) 的概率方程 \(f\) 來描述,那麼這個包含兩個參數的概率方程的似然和對數似然分別是:
\[ \begin{aligned} L(\theta, \phi | \underline{x}) &= \prod_{i=1}^nf(x_i | \theta, \phi) \\ \ell(\theta, \phi | \underline{x}) &= \sum_{i=1}^n\text{log}f(x_i | \theta, \phi) \end{aligned} \]
兩個參數的 \(\text{MLE}\) 可以通過對對數似然方程進行兩次偏微分,然後解連立方程組:
\[ \left\{ \begin{array}{ll} \frac{\partial\ell}{\partial\theta} = 0\\ \frac{\partial\ell}{\partial\phi} = 0 \\ \end{array} \right. \]
17.3.2 兩組數據各一個參數
如果是兩組獨立數據,各由一個參數描述他們各自的概率方程:
\[ X_1, \cdots, X_n \stackrel{i.i.d}\sim f(\theta_1) \\ Y_1, \cdots, Y_m \stackrel{i.i.d}\sim f(\theta_2) \]
那麼以兩組數據爲聯合條件 (應該可以理解爲同時觀察到時的) 的聯合似然 (joint likelihood):
We describe the likelihood as the joint likelihood, conditional on jointly observing both datasets:
\[ L(\theta_1, \theta_2|\underline{x},\underline{y}) = \prod_{i=1}^nf_1(x_{1i}|\theta_1) \times \prod_{i=1}^mf_2(y_{i}|\theta_2) \]
所以,聯合之後的對數似然方程就是兩個對數似然方程之和:
\[ \ell(\theta_1,\theta_2|\underline{x},\underline{y}) = \sum_{i=1}^n\text{log} f(x_i|\theta_1) + \sum_{i=1}^m\text{log} f(y_i|\theta_2) \]
你會發現,分成兩組數據兩個獨立的概率方程之後的聯合對數似然方程求 \(\text{MLE}\) 時需要用偏微分。可是偏微分之後的結果,和兩組數據合二爲一,用含有兩個參數的概率方程,計算其 \(\text{MLE}\) 的結果會完全相同。
17.4 正態分佈概率密度方程中總體均值和方差都未知 (單樣本 \(t\) 檢驗 one sample \(t\) test 的統計學推導)
此時的情況如同前面的把兩組數據合二爲一的情況,用正態分佈的概率方程,然後有兩個參數 \(\mu, \sigma^2\)。
\[ Y_1,\cdots,Y_n \stackrel{i.i.d}{\sim} N(\mu, \sigma^2) \\ \ell(\mu, \sigma^2 | \underline{y}) = -\frac{n}{2}\text{log}\sigma^2 - \frac{1}{2\sigma^2}\sum^n_{i=1} (x_i - \mu)^2 \]
\[ \begin{aligned} & \mu: \frac{\partial \ell}{\partial \mu} = \frac{\sum^n_{i=1}(y_i-\mu)}{2\sigma^2} = 0 \Rightarrow \hat\mu = \bar{y}\\ & \sigma^2: \frac{\partial \ell}{\partial (\sigma^2)} = -\frac{n}{2\sigma^2} + \frac{1}{2(\sigma^2)^2}\sum^n_{i=1}(y_i-\mu)^2 \\ & \text{ Substituting } \mu=\hat\mu = \bar{y} \text{ and set equal to } 0\\ & \frac{n}{2\sigma^2} + \frac{1}{2(\sigma^2)^2}\sum^n_{i=1}(y_i-\bar{y})^2 = 0 \\ & \Rightarrow \hat\sigma^2 = \frac{1}{n}\sum^n_{i=1}(y_i - \bar{y})^2 \end{aligned} \]
有沒有覺得這裏的方差的極大似然估計似曾相識 (Section 10.3)。在早期的章節中,我們學到了分部法 (“把樣本和總體均值之間的差的平方和分成兩部分”):
\[ \begin{aligned} \sum^n_{i=1}(y_i-\mu)^2 & = \sum^n_{i=1}(y_i - \bar{y} + \bar{y} -\mu)^2 \\ & = \sum^n_{i=1}(y_i - \bar{y})^2 + \sum^n_{i=1}(\bar{y}-\mu)^2 \\ \Rightarrow \sum^n_{i=1}(y_i - \bar{y})^2 & = \sum^n_{i=1}(y_i-\mu)^2 - \sum^n_{i=1}(\bar{y}-\mu)^2 \end{aligned} \]
當時分的是平方和,這裏再介紹一種把概率分部的方法 partition the probabilities。
We can “partition” the probability of observing the data, conditional on unknown \(\mu\) and \(\sigma^2\), into
- the probability of observing the data conditional on the observed sample mean \(\bar{y}\) and unknown \(\sigma^2\) ;
- the probability of observing the sample mean \(\bar{y}\) conditional on the two unknown parameters.
\[ \begin{aligned} & \text{Prob}(\underline{y} | \mu, \sigma^2) = \text{Prob}(\underline{y}|\bar{y}, \sigma^2) \times \text{Prob}(\bar{y}|\mu, \sigma^2) \\ &\Rightarrow \text{Prob}(\underline{y} | \bar{y}, \sigma^2) = \frac{\text{Prob}(\underline{y} | \mu, \sigma^2)}{\text{Prob}(\bar{y}|\mu, \sigma^2)} \end{aligned} \]
看到這裏你是否會想起概率論中討論的條件概率方程 (Section 1.2):
\[ f(x|Y=y) = \frac{f(x,y)}{f(y)} \]
利用上述概率分佈的方法,我們可以進而推導方差 \(\sigma^2\) 的 \(\text{MLE}\):
\[ \begin{aligned} f(\underline{y} | \bar{y}, \sigma^2) &= \frac{ \color{red}{f(\underline{y} | \mu, \sigma^2)} }{f(\bar{y}|\mu, \sigma^2)} \\ &= \frac{ \color{red}{(\frac{1}{\sqrt{2\pi\sigma^2}})^ne^{-\frac{1}{2\sigma^2}\sum^n_{i=1}(y_i - \mu)^2}} }{(\frac{1}{\sqrt{2\pi\sigma^2/n}})e^{-\frac{1}{2\sigma^2/n}(\bar{y}-\mu)^2}} \\ \Rightarrow \ell(\sigma^2| \underline{y}, \bar{y}) &= \color{red}{-\frac{n}{2}\text{log}\sigma^2 - \frac{1}{2\sigma^2}\sum^n_{i=1}(y_i-\mu)^2} \\ & \;\;\;+\frac{1}{2}\text{log}\frac{\sigma^2}{n} + \frac{1}{2\sigma^2/n}(\bar{y}-\mu)^2 \\ &= -\frac{n-1}{2}\text{log}\sigma^2 - \frac{1}{2\sigma^2}(\sum^n_{i=1}(y_i-\mu)^2 - n(\bar{y}-\mu)^2) \\ \text{Because } &\sum^n_{i=1}(y_i - \bar{y})^2 = \sum^n_{i=1}(y_i-\mu)^2 - \sum^n_{i=1}(\bar{y}-\mu)^2 \\ \Rightarrow \ell(\sigma^2| \underline{y}, \bar{y}) &= -\frac{n-1}{2}\text{log}\sigma^2 -\frac{1}{2\sigma^2}\sum^n_{i=1}(y_i - \bar{y})^2 \\ \text{Note that the } &\text{above conditional log-likelihood is now free of } \mu \\ \Rightarrow \ell^\prime(\sigma^2) &= -\frac{n-1}{2\sigma^2} + \frac{1}{2(\sigma^2)^2}\sum^n_{i=1}(y_i-\bar{y})^2 \\ \text{Set equal } & \text{to zero and rearrange} \\ \Rightarrow \hat\sigma^2 &= \frac{1}{n-1}\sum^n_{i=1}(y_i-\bar{y})^2\\ \text{This is the } &\color{red}{\text{unbiased estimate of } \sigma^2} \end{aligned} \]
現在再重新考慮對數據 \(Y_1, \cdots, Y_n \stackrel{i.i.d}{\sim} N(\mu, \sigma^2)\) 進行均值的假設檢驗:
\[ \text{H}_0: \mu = \mu_0 \text{ v.s H}_1: \mu > \mu_0 \]
當 \(\sigma^2\) 是已知的,在零假設條件下的檢驗統計量是:
\[ \begin{aligned} & \text{H}_0 \Rightarrow (\frac{\bar{Y}-\mu_0}{\sigma/\sqrt{n}}) \sim N(0,1) \\ & \text{Or equivalently, } \\ & (\frac{\bar{Y}-\mu_0}{\sigma/\sqrt{n}})^2 \sim \chi_1^2 \end{aligned} \tag{17.1} \]
當 \(\sigma^2\) 是未知的,它需要通過樣本數據來估計時。我們就該使用前面從條件對數似然方程推導出的方差無偏估計:
\[ \hat\sigma^2 = S^2 = \frac{1}{n-1}\sum^n_{i=1}(y_i-\bar{y})^2 \]
但是,假如只把無偏估計的方差放到公式 (17.1) 裏去,可以當作新的檢驗統計量嗎?有這麼簡單嗎?
\[ (\frac{\bar{Y}-\mu_0}{s/\sqrt{n}})^2 \]
當然沒有這麼簡單!這種方式僅僅考慮了樣本的方差估計,卻忽略了這個估計是有不確定性的 (uncertainty),它並不是真實的 \(\sigma^2\),只是個估計 (estimator)。我們需要找到一種方法把方差的不確定性也考慮進新的檢驗統計量裏去。利用章節 10.4 的結論:
\[ \begin{equation} \frac{n-1}{\sigma^2}S^2 \sim \chi^2_{n-1}\\ \Rightarrow \frac{S^2}{\sigma^2} = \frac{\chi^2_{n-1}}{n-1} \end{equation} \tag{17.2} \]
\[ \frac{(\bar{Y}-\mu_0)^2}{S^2/n} \sim \frac{\chi^2_1/1}{\chi^2_{n-1}/n-1} = F_{1,n-1} \]
這樣我們就同時考慮了方差估計本身,和它的不確定性了。這個新的統計量被定義爲 \(T\):
\[ \begin{aligned} & T=\frac{\bar{Y}-\mu_0}{S/\sqrt{n}} \\ & \text{Then under H}_0: T^2 \sim F_{1,n-1} \text{ or equivalently } T \sim \sqrt{F_{1,n-1}}=t_{n-1} \end{aligned} \]
這個特殊的 \(F\) 分佈,就是我們之前定義過的,這裏用手紮紮實實地推導出來的檢驗統計量 \(t\) 和 \(t\) 分佈。利用這個方差未知時的分佈,均值的 \(95\%\) 信賴區間的估計就是:
\[ 95\% \text{ CI for } \mu: \bar{Y} \pm t_{n-1,0.975}\frac{S}{\sqrt{n}} \]
17.5 比較兩組獨立數據的均值 two sample \(t\) test with equal unknown \(\sigma^2\)
本節要來推導方差齊時的兩個獨立樣本的均值比較 two sample \(t\) test。兩個獨立樣本用下面的數學符號標記:
\[ X_1, \cdots, X_n \stackrel{i.i.d}{\sim} N(\mu_1, \sigma^2); Y_1, \cdots, Y_m, \stackrel{i.i.d}{\sim} N(\mu_2, \sigma^2) \]
要進行的假設檢驗是:
\[ \text{H}_0: \mu_1 = \mu_2 \text{ v.s. } \text{H}_1: \mu_1 > \mu_2 \]
此時,兩組獨立樣本的共同方差 \(\hat\sigma^2\) 需要被估計,利用上面相同的推導過程,可以獲得合併後的共同方差的無偏估計:
\[ \begin{equation} \hat\sigma^2 = S^2_p = \frac{\sum^n_{i=1}(X_i-\bar{X})^2 + \sum^m_{i=1}(Y_i-\bar{Y})^2}{n+m-2}\\ \end{equation} \tag{17.3} \]
因爲兩組數據互相獨立,所以有:
\[ \begin{aligned} & \frac{1}{\sigma^2}\sum^n_{i=1}(X_i - \bar{X})^2 \sim \chi^2_{n-1} \\ & \frac{1}{\sigma^2}\sum^m_{i=1}(Y_i - \bar{Y})^2 \sim \chi^2_{m-1} \\ \Rightarrow &\frac{1}{\sigma^2}\{ \sum^n_{i=1}(X_i - \bar{X})^2 + \sum^m_{i=1}(Y_i - \bar{Y})^2 \} \sim \chi^2_{n+m-2} \end{aligned} \]
把公式 (17.3) 代入此式可得:
\[ \begin{equation} (n+m-2)\frac{S^2_p}{\sigma^2} \sim \chi^2_{n+m-2} \end{equation} \tag{17.4} \]
由於 \(\bar{X} \sim N(\mu_1, \frac{\sigma^2}{n}); \bar{Y} \sim N(\mu_2, \frac{\sigma^2}{m})\),所以在零假設條件下 \(\text{H}_0: \mu_1=\mu_2\Rightarrow \bar{X}-\bar{Y} \sim N(0,\sigma^2(\frac{1}{n}+\frac{1}{m}))\)。
\[ \begin{equation} \Rightarrow \frac{\bar{X}-\bar{Y}}{\sqrt{\sigma^2(\frac{1}{n}+\frac{1}{m})}} \sim N(0,1) \\ \Leftrightarrow \frac{(\bar{X}-\bar{Y})^2}{\sigma^2(\frac{1}{n}+\frac{1}{m})} \sim \chi^2_1 \end{equation} \tag{17.5} \]
\[ \begin{aligned} &\frac{(\bar{X}-\bar{Y})^2}{\sigma^2(\frac{1}{n}+\frac{1}{m})} \times \frac{\sigma^2}{S^2_p(n+m-2)} = \frac{\chi^2_1/1}{\chi^2_{n+m-2}} \\ &\Rightarrow T^2 = \frac{(\bar{X}-\bar{Y})^2}{S^2_p(\frac{1}{n}+\frac{1}{m})} = \frac{\chi^2_1/1}{\chi^2_{n+m-2}/(n+m-2)} \sim F_{1,n+m-2} \\ &\Rightarrow T = \frac{\bar{X}-\bar{Y}}{S_p\sqrt{\frac{1}{n}+\frac{1}{m}}} \sim t_{n+m-2} \end{aligned} \]
這就是標準的兩個齊方差的獨立樣本均值比較的 \(t\) 檢驗,two-sample \(t\) test with pooled variance。這裏推導的兩個 \(t\) 檢驗,是都是精確的似然比檢驗 (likelihood ratio test) (Section 16.2)。壯士請自己跟着似然比檢驗的方法推導一次。