第 23 章 假設檢驗
23.1 拋硬幣的例子
對數據進行假設檢驗是統計分析最重要的部分。一般進行實驗或者調查時我們會先設定一個零假設。假如實驗或者調查中獲得的一系列數據可以認爲是相互獨立且隨機地從人羣中抽取的樣本,那麼根據零假設爲真的條件,樣本數據提供的參數估計和零假設條件下的參數應該是差距不大 (一致) 的。因爲概率論環境下,我們用樣本數據來作假設檢驗,如果樣本提供的數值比起零假設條件下的參數大很多或者小很多,我們就有理由,有證據拒絕零假設。
下面用投硬幣作爲例子說明。硬幣如果是公平的,那麼拋硬幣後正反面出現的概率應該一樣,都是 \(50\%\) (零假設:\(p=0.5\))。假如有一枚硬幣,拋了 \(10\) 次只有一次是反面朝上的,我們可能就會懷疑,這枚資本主義硬幣一定是被做了手腳 (變得不再公平了),這就是通過實驗質疑和挑戰零假設的思想。如此粗糙的想法卻是統計學假設檢驗的理論起源。只是在統計學裏面,需要制定一些規則來規定,實驗數據跟零假設 (設想) 差異達到多大時 (檢驗),認爲證據足夠達到相信零假設“非真” (挑戰權威)。
檢驗的過程,就是計算我們朝思暮想的 \(p\) 值。\(p\) 值的定義是,當零假設爲真時,我們觀察到的實驗結果以及比這個結果更加極端 (雙側) 的情況在所有可能的情況中出現的概率。繼續使用拋硬幣的例子來說的話,跟 “\(10\) 次拋硬幣出現一次反面朝上” 一樣極端或者更加極端的事件有:
- “一次反面朝上”,
- “零次反面朝上”,
- “九次反面朝上 (或者說一次正面朝上)”,
- “十次反面朝上 (或者說零次正面朝上)”。
相反地,沒有觀察事件 “\(10\) 次拋硬幣出現一次反面朝上” 那麼極端的事件就包括了:
- “兩次反面朝上”,
- “三次反面朝上”,
- “四次反面朝上”,
- “五次反面朝上”,
- “六次反面朝上”,
- “七次反面朝上”,
- “八次反面朝上”。
檢驗的過程我們會定義一個被檢驗的統計量,一般就是我們感興趣的參數的估計 (estimator of a parameter of interest)。在上面拋硬幣的例子中,這個檢驗統計量就是 “硬幣反面朝上的次數”。觀察到的反面朝上次數除以拋硬幣次數 (\(10\) 次) 就是獲得硬幣反面朝上的概率 (參數) 的估計。用 \(R\) 表示十次拋硬幣中觀察到反面朝上的次數,那麼此時 \(R\) 就是一個服從二項分佈的隨機變量,其服從的二項分佈成功 (反面朝上事件發生) 的概率 (參數) 是\(\pi\)。所以某一次實驗中 (拋十次硬幣算一次實驗),\(R=r\),那麼這次試驗的參數估計的 \(p\) 值被定義爲:
\[ \begin{equation} \text{Prob}\{ R \text{ as or more extreme than } r | \pi=0.5 \} \end{equation} \tag{23.1} \]
零假設:反面朝上出現的概率是 \(\pi=0.5\);替代假設: \(\pi\neq 0.5\)。當零假設爲真時,\(R\sim \text{Bin}(10, 0.5)\),它的零假設分佈如下圖 23.1:
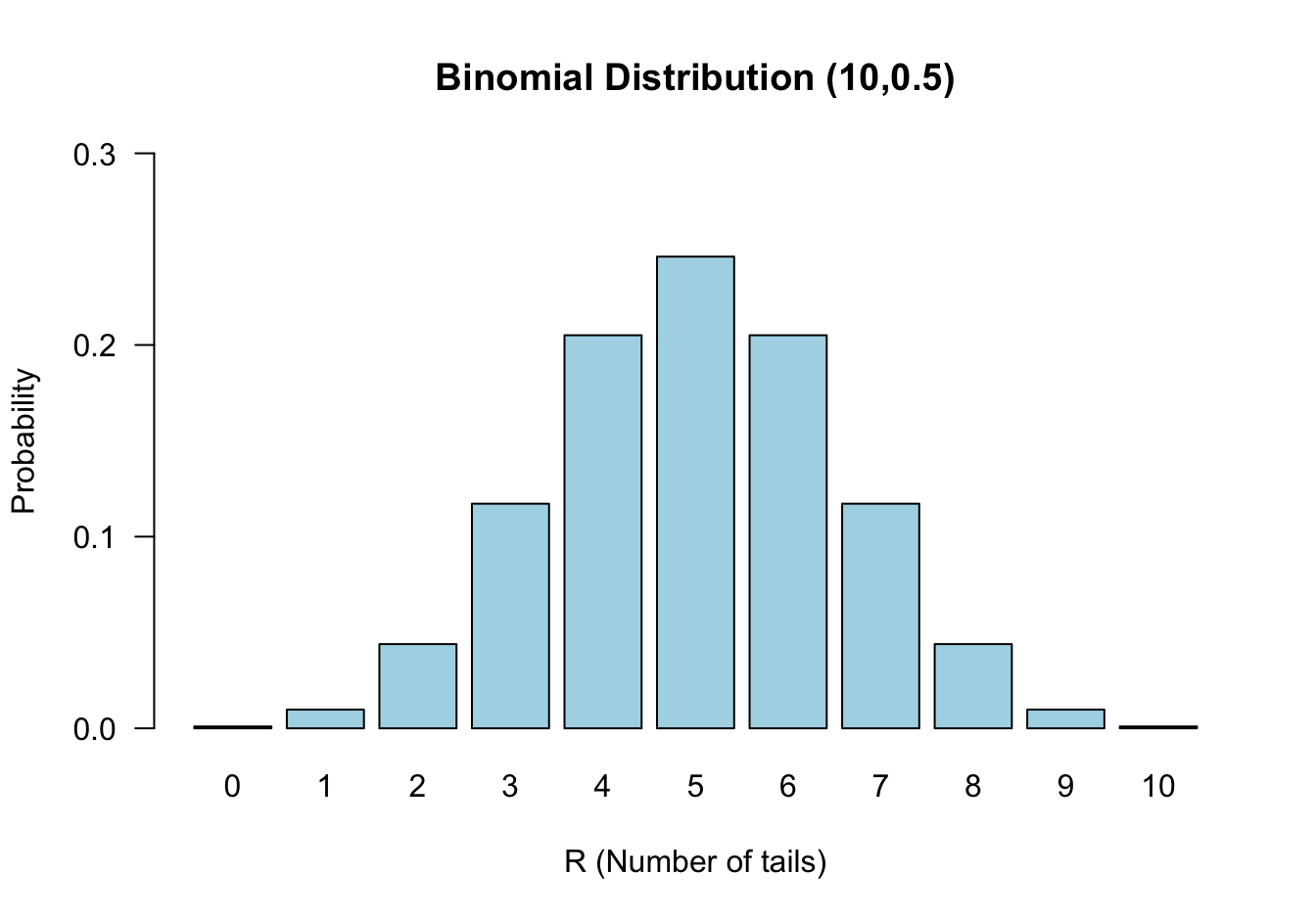
圖 23.1: Binomial distribution n=10, π = 0.5
本節拋硬幣的例子我們觀察到十次拋硬幣只有一次反面朝上,\(r=1\)。其發生的概率等於上面列舉的四種與之同等極端或者更加極端的情況發生概率之和:
\[ \begin{aligned} &\text{Prob} \{R=0|\pi=0.5\} + \text{Prob} \{R=1|\pi=0.5\} + \text{Prob} \{R=9|\pi=0.5\} + \text{Prob} \{R=10|\pi=0.5\} \\ & = (\binom{10}{0} + \binom{10}{1} + \binom{10}{9} + \binom{10}{10})\times(0.5)^{10} = 0.021 \end{aligned} \]
23.1.1 單側和雙側檢驗
在上面的例子中其實我們已經用到了雙側檢驗的概念。例如,我們把 “九次反面朝上” 事件發生的概率當作和 “一次反面朝上” 事件發生的概率具有同等 “極端”概率事件,但是其實在圖 23.1 中也能看出兩種事件發生的方向是在概率分佈的左右兩側,這就是典型的雙側檢驗思想。一個“單側”檢驗則不考慮另一個方向發生的極端事件。
還是用本節的例子,如果要計算單側檢驗 \(p\) 值:
\[ \begin{aligned} &\text{Prob}\{R\leqslant r| \pi=0.5\}\\ &\text{In the example } r=1 \\ &\Rightarrow \text{Prob}\{R=0 | \pi = 0.5\} + \text{Prob}\{ R=1 | \pi = 0.5 \} = 0.011 \end{aligned} \]
此時零假設爲 \(\pi=0.5\),替代假設爲 \(\pi < 0.5\)。
大多數時候,單側檢驗的 \(p\) 值十分接近雙側檢驗 \(p\) 值的一半。但是實施單側假設檢驗的前提是,我們有絕對的把握事件不會發生另一個方向上,但是這種情況少之又少,所以基本上你能看到的絕大多數假設檢驗計算的 \(p\) 值都是雙側檢驗 \(p\) 值。
23.1.2 \(p\) 值的意義
假設檢驗被認爲是作決策的一種手段。你會看到一些人使用 \(0.05\) 作閾值來作爲拒絕 (\(<0.05\)) 或接受 (\(>0.05\)) 零假設的依據。許多醫學實驗,醫學研究的結果確實是用來作決策的依據。例如某個臨牀試驗用隨機雙盲對照實驗法比較新藥物和已有藥物對某種疾病的治療效果差異,通過實驗結果來決定是否向市場和患者推廣新的治療藥物,此時 \(p\) 值的大小就是作決斷的重大依據。然而還有另外的很多實驗/研究並非爲了作什麼直接的決策,可能只是爲了更多的瞭解疾病發生的原因和機制。例如可能乳腺癌多發在女性少發在男性人羣,這顯然是十分顯著的差異,但是這種結果不能讓我們決策說要不要改變一個人的性別,而只是提供了疾病發生發展過程的機理上的證據。因此,許多研究者主張把 \(p\) 值大小當作是反對零假設證據的強弱指標。但是此處要指出的是,並非所有統計學家都認同 \(p\) 值大小真的可以度量證據的強弱水平。
所以,建議在寫論文,作報告時,儘量避免說:“本次實驗研究結果具有顯著的統計學意義,there was evidence that the result was statistically significant”。建議使用的語言類似這樣:“在顯著性水平爲 5% 時,本研究結果達到了統計學意義,statistically significant at the 5% level”;或者 “在顯著性水平爲 5% 時,我們的研究提供了足夠的證據證明零假設是不正確的,there was evidence that at the 5% level, that the hypothesis being tested was incorrect”。
如果一個實驗結果 \(p\) 值大於 0.05,可以被解讀爲:實驗結果不能提供足夠的證據證明零假設是錯誤的,there was no (or insufficient) evidence against the null hypothesis。另外還有一些人會使用一些詞語來描述 \(p\) 值大小:如果 \(p=0.0001\),可能會被解讀爲實驗提供了“強有力的證據”,反對零假設;如果 \(p=0.06; p=0.04\),會被人解讀爲是具有“臨界統計學意義,borderline statistically significant”,或者試驗結果提供了“一些證據,some evidence” 反對零假設。
23.2 二項分佈的精確假設檢驗
若 \(n\) 次實驗中成功次數爲 \(R\),那麼樣本百分比 (估計,estimator) \(P=\frac{R}{n}\) 是它的人羣比例 \(\pi\) (參數,parameter) 的無偏估計。欲檢驗的零假設 \(\pi=\pi_0\),替代假設 \(\pi\neq\pi_0\),且某一次觀察結果爲 \(R=r\),我們要計算的 \(p\) 值就是在零假設條件下,所有情況中 \(R=r\) 或者與之同等極端甚至更加極端的事件所佔的比例。
- 如果 \(r<n\pi_0\),單側 \(p\) 值等於
\[ \begin{aligned} p & = \text{Prob}\{ r\text{ or fewer successes out of n | \pi=\pi_0} \} \\ & = P_0 + P_1 + P_2 + \cdots + P_r \\ \text{Where } & P_x = \binom{n}{x} \pi_0^x (1-\pi_0)^{n-x} \end{aligned} \]
- 如果 \(r>n\pi_0\),單側 \(p\) 值等於
\[ \begin{aligned} p & = \text{Prob}\{ r\text{ or more successes out of n | \pi=\pi_0} \} \\ & = P_r + P_{r+1} + P_{r+2} + \cdots + P_{n} \\ \text{Where } & P_x = \binom{n}{x} \pi_0^x (1-\pi_0)^{n-x} \end{aligned} \]
一般情況下兩個單側 \(p\) 值很接近,所以雙側 \(p\) 值就可以計算其中一個然後乘以 \(2\)。你也可以計算兩側的單側 \(p\) 值然後相加。
23.3 當樣本量較大
如果樣本量 \(n\) 比較大,那麼計算上面的精確法是十分繁瑣的 (計算器也會累。。。)。可以考慮利用中心極限定理用正態近似法進行假設檢驗。此時需要做的就是把近似後的正態分佈標準化,然後和標準正態分佈做比較獲得 \(p\) 值即可:
\[ \begin{equation} Z=\frac{R-E(R)}{\sqrt{\text{Var}(R)}} = \frac{R-E(R)}{\text{SE}(R)} \end{equation} \tag{23.2} \]
在目前爲止人類所知道的範圍內,上面公式的 \(Z\) 值隨着實驗樣本量 \(n\) 的增加而無限接近標準正態分佈 \(N(0,1)\)。
23.4 二項分佈的正態近似法假設檢驗
二項分佈的特徵值:
\[ E(R) = n\pi_0; \text{ and Var}(R) = n\pi_0(1-\pi_0) \]
套用公式 (23.2),計算 \(Z\) 值如下:
\[ \begin{aligned} Z & = \frac{R-E(R)}{\sqrt{\text{Var}(R)}} \\ & = \frac{R-n\pi_0}{\sqrt{n\pi_0(1-\pi_0)}} \\ & = \frac{P-\pi_0}{\sqrt{\frac{\pi_0(1-\pi_0)}{n}}} \\ \text{Where } & P=\frac{R}{n} \end{aligned} \]
利用實驗數據的 \(p=r/n\),以及零假設時的 \(\pi_0\),就可以計算上面的觀察 \(Z\) 值,之後查閱標準正態分佈的概率表格就可以獲得單側 \(p\) 值,別忘了乘以 \(2\)。
23.4.1 連續性校正 continuity correction
在使用正態分佈近似法進行二項分佈數據的假設檢驗時,我們其實是在使用一個連續型分佈近似一個離散型分佈,誤差通常會比較大。我們會使用矯正後的正態近似法計算 \(Z\) 值:
\[ Z=\frac{|R-n\pi_0|-\frac{1}{2}}{\sqrt{n\pi_0(1-\pi_0)}} \text{ or } Z=\frac{|P-\pi_0|-\frac{1}{2n}}{\sqrt{\frac{\pi_0(1-\pi_0)}{n}}} \]
“Statistical Methods in Medical Research” (Armitage, Berry, and Matthews 2008) 書中建議,滿足 \(n\pi \geqslant 10 \text{ or } n(1-\pi) \geqslant 10\) 時近似法計算的 \(p\) 值可以給出較爲滿意的結果。另外,當 \(n>100\) 則建議不再進行連續性校正,即把校正部分的 \(-\frac{1}{2}\) 或者 \(-\frac{1}{2n}\) 去掉。
23.5 情況1:對均值進行假設檢驗 (方差已知)
假設從已知方差 \((\sigma^2)\) 的人羣中隨機抽取樣本進行血糖值測量 \((Y_n)\),該樣本測量的人羣的平均血糖值爲 \(\mu=\bar{Y}\),假設我們要比較該人羣的血糖值和某個理想血糖值 \(\mu_0\),進行假設檢驗:
\[\text{H}_0: \mu=\mu_0 \text{ v.s. H}_1: \mu\neq\mu_0\]
根據中心極限定理,當 \(n\) 足夠大,樣本均值 \(\bar{Y}\) 的分佈接近正態分佈,且均值 \(\mu\),方差 \(\frac{\sigma^2}{n}\)。所以可以計算 \(Z\) 值:
\[ Z = \frac{\bar{Y}-E(\bar{Y})}{\sqrt{\text{Var}\bar{Y}}} = \frac{\bar{Y}-\mu_0}{\sqrt{\sigma^2/n}} \]
進而計算其 \(p\) 值:
\[ \begin{aligned} p &= \text{Prob}(\bar{Y}\leqslant\bar{y}|\mu=\mu_0) \\ &= \text{Prob}(Z<\frac{\bar{y}-\mu_0}{\sqrt{\sigma^2/n}}) \\ &= \Phi(\frac{\bar{y}-\mu_0}{\sqrt{\sigma^2/n}}) \\ \text{Where } & \Phi \text{ is the distribution function for a } N(0,1) \text{distribution} \end{aligned} \]
所以計算了上面的單側 \(p\) 值以後別忘了乘以 \(2\) 以獲得雙側 \(p\) 值:
\[ \text{Two-sided } p \text{ value } = 2\times[1-\Phi(\frac{\bar{y}-\mu_0}{\sqrt{\sigma^2/n}})] \]
23.6 情況2:對均值進行假設檢驗 (方差未知) the one-sample t-test
如果方差未知,我們仍要比較一個樣本均值和一個數值的話,零假設和替代假設依然不變:
\[\text{H}_0: \mu=\mu_0 \text{ v.s. H}_1: \mu\neq\mu_0\]
但是此時計算的統計量的分母,總體方差的地方使用了樣本方差 \(\frac{\hat\sigma^2}{n}\) 替代時,該統計量不再服從標準正態分佈,而服從自由度爲 \(n-1\) 的 \(t\) 分佈。\(t\) 分佈看上去和標準正態分佈很像,但是其分佈的雙側尾部“較厚”,峯度大於 3:
\[ T = \frac{\bar{Y}-\mu_0}{\sqrt{\hat\sigma^2/n}} \sim t_{n-1} \]
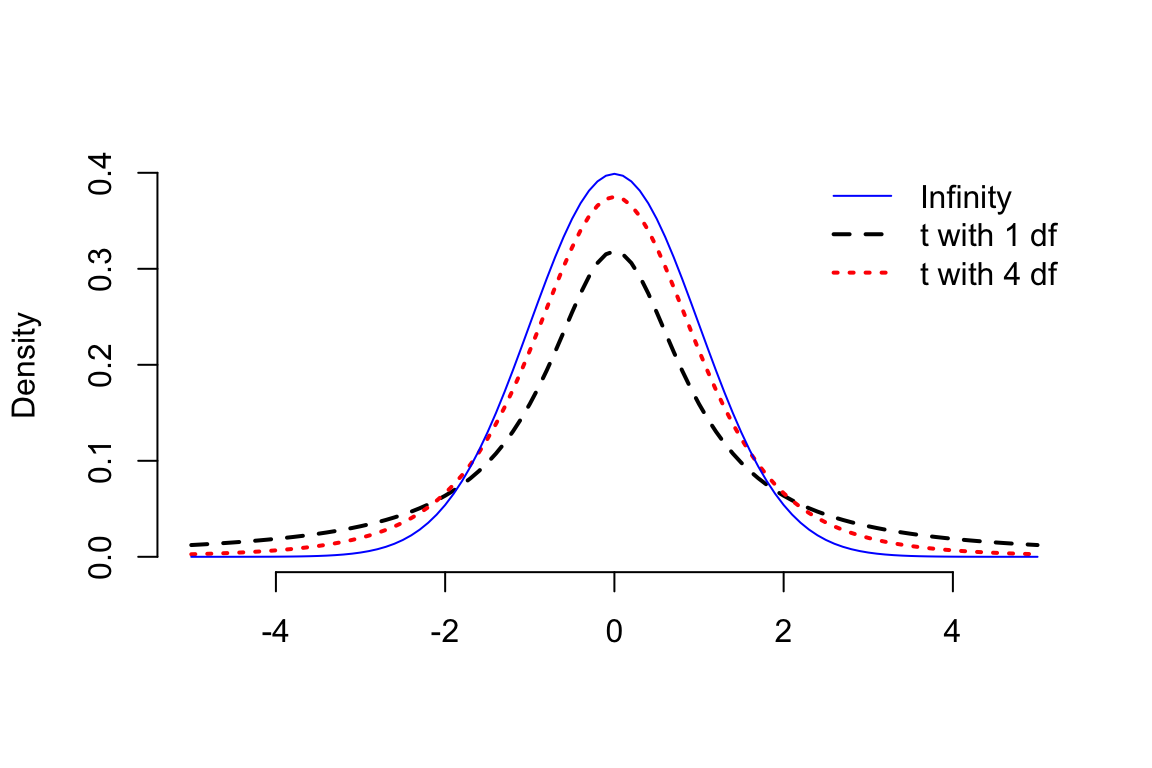
圖 23.2: Student t distributions with 1, 4 and infinity degrees of freedom compared with a standard normal distribution