第 43 章 貝葉斯理論在正態分布數據中的應用 Normal distribution applying Bayes’ Theorem

… every now and then delightful ideas spring to view; the idea that we shall all be Bayesian by 2020…

– D.V. Lindley (1973)4

43.1 事後概率的總結方法

在貝葉斯統計推斷中，如何總結和報告計算獲得的事後概率分布呢？首先想到的大概是均值 (mean)，因爲均值不論在貝葉斯還是傳統的概率論統計學中都是十分有效的描述數據的一個指標，特別是當後驗概率分布本身是左右對稱的時候。事實上，類似概率論統計學觀點，貝葉斯學派裏中心極限定理同樣是適用的。也就是說，無論先驗概率是怎樣的分布，當收集的樣本足夠多，其事後概率的分布均可被認爲趨近於正態分布:

  • 貝葉斯中心極限定理 Bayesian Central limit theorem:

\[ (\frac{\theta - \text{E}[\theta|y]}{\sqrt{\text{Var}(\theta|y)}}) \rightarrow N(0,1) \]

  • 貝葉斯後驗概率獨立性定理 Berstein-von Mises theorem: 這條定理說的是，當樣本量十分巨大時，後驗概率其實和 “我們認爲” 的先驗概率之間是相互獨立的。也就是說，數據足夠多的時候，似然本身起到了最主導的作用，先驗概率的取值變得不再那麼重要。

所以，當你擁有足夠多的數據的時候，完全可以理直氣壯地直接使用這個中心極限定理，用均值方差就能準確地描述事後概率分布。

除了均值和方差可以用於描述事後概率分布。要記住，在寫報告的時候，我們應當先把事後概率分布給繪制出來，看看實際的圖形是怎樣的，計算一下其四分位數都是些怎樣的數值，如果這些描述提示計算獲得的事後概率分布不能被認爲是左右對稱的時候，僅僅只匯報均值和方差就顯得有些偏頗。如果事後概率分布的密度分布圖告訴我們它並不能用正態分布來近似的話，我們就應該報告包括均值在內的衆數，中位數，以及其他的百分位數，用於更加精確地描述事後概率分布。

除此之外，我們還可以報告可信區間 (credible intervals)。這個可信區間，和信賴區間相似地，是一個有上限和下限的範圍。用 \(\alpha \in (0,1)\) 表示我們的可信程度，可信區間 \(I\) 的上限和下線分別用 \(U, L\) 來表示，那麼用某個參數 \(\theta\) 描述的事後概率，以及 \(\alpha\) 之間的關系就是:

\[ \text{Pr}(\theta \in I | \text{Data}) = \int_L^U\pi(\theta | \text{Data}) = \alpha \]

但是值得注意的是，和概率論信賴區間的 “一次實驗只計算一個信賴區間” 不同，貝葉斯可以計算完整的事後概率分布曲線，所以整個分布上包含了 95% 曲線下面積我們其實可以獲得無數個不同長度大小的可信區間。在這些許許多多的可信區間裏面，我們可以找到一個上下限之間距離最短的可信區間，名之爲最高密度事後概率區間 (the Highest Posterior Density, HPD interval)。如果事後概率分布是標準正態分布，那麼其 95% HPD 區間就是 \((-1.96, 1.96)\)。

43.2 貝葉斯統計推斷中的正態分布

本章節我們只考慮最最簡單的情形，方差已知的正態分布數據。在這裏，只有一個參數–均值 \(\mu\) ，且我們用另一個方式來標記方差: \(y \sim N(\mu, \sigma^2 = \tau^{-1})\)。如果參數 \(\mu\) 的先驗概率分布的均值是 \(\nu\)，精確度 (precision, 等同於方差的倒數) 是 \(\gamma\)。

那麼應用貝葉斯定理推導有:

\[ \begin{aligned} \text{Posterior} & = \text{Prior}\times\text{likelihood} \\ \pi(\mu|y) & = \sqrt{\frac{\gamma}{2\pi}}\text{exp}\{ -\frac{\gamma}{2}(\mu - \nu)^2 \} \times\sqrt{\frac{\tau}{2\pi}}\text{exp}\{ -\frac{\tau}{2}(y - \mu)^2 \} \\ & \propto \text{exp}\{ -\frac{\tau}{2}(y - \mu)^2 - \frac{\gamma}{2}(\mu - \nu)^2\} \\ & \propto \text{exp}\{ -\frac{1}{2}[(\tau + \gamma)\mu^2 - 2(\tau y + \nu\gamma)\mu] \} \\ & \propto \text{exp}\{ -\frac{(\tau+\gamma)}{2}(\mu - \frac{\tau y + \nu\gamma}{\tau + \gamma})^2 \} \\ & \propto N\{ \frac{\tau y+ \gamma\nu}{\tau + \gamma}, \text{precision} = (\tau + \gamma) \} \end{aligned} \tag{43.1} \]

可以看出，正態分布本身是自己的共軛分布 (先驗概率分布是正態分布的，事後概率分布也服從正態分布)。事後概率分布的精確度 (precision) 就等於先驗概率的精確度和似然方程的精確度之和。其均值則等於數據本身的均值和先驗概率均值乘以權重之和，其各自的權重分別是彼此精確度在兩個精確度之和中所佔的比例。

現在假設手頭我們收集到的數據服從標準正態分布 \(N(\mu=0,\sigma^2 = \tau^{-1} = 1)\)，圖 43.1 展示了四種似然方程，先驗概率，和事後概率分布的組合圖。

  1. 圖 43.1 的左上角中，先驗概率均值，精確度分別是 \(\nu = 0, \gamma = 1/16\) (精確度 \(1/16\) 等同於標準差等於 \(4\))。可以看出這個先驗概率幾乎對數據提供的似然方程毫無影響。事後概率分布計算的 HPD 可信區間，將會和數據提供的似然方程計算獲得的信賴區間十分地接近 (因爲他們二者的圖形幾乎是重疊的，不過要記得他們各自的含義不同)。
  2. 圖 43.1 的右上角中，先驗概率均值被設定爲 \(\nu = 2\)，精確度不變。可以確認就是和左上角圖顯示的類似，此時的先驗概率對事後概率的分布影響十分有限。
  3. 圖 43.1 的左下角中，先驗概率分布的均值和精確度被設定爲 \(\nu = 2, \gamma = 1\)，精確度變得和似然方程是相同的，所以，事後概率分布的均值，精確度分別是 \(1, 2\)，所以此時事後概率分布的標準差是 \(1/\sqrt{2}\)。由於先驗概率分布和數據的似然方程提供的信息旗鼓相當，事後概率分布就落在了二者之間，但是值得注意的是，事後概率分布估計的精確度比似然方程本身好了一些 (數據結合了先驗概率信息，所以用於估計的信息量增加，精確度自然就增加)。
  4. 圖 43.1 的右下角中，先驗概率分布變成了主導，因爲它的均值和精確度分別是 \(\nu = 3, \gamma = 8\)。可以看到事後概率分布由於先驗概率分布佔據了主導而被先驗概率分布拉向了右邊，此時的數據提供的信息相對先驗概率分布的信息權重較低。
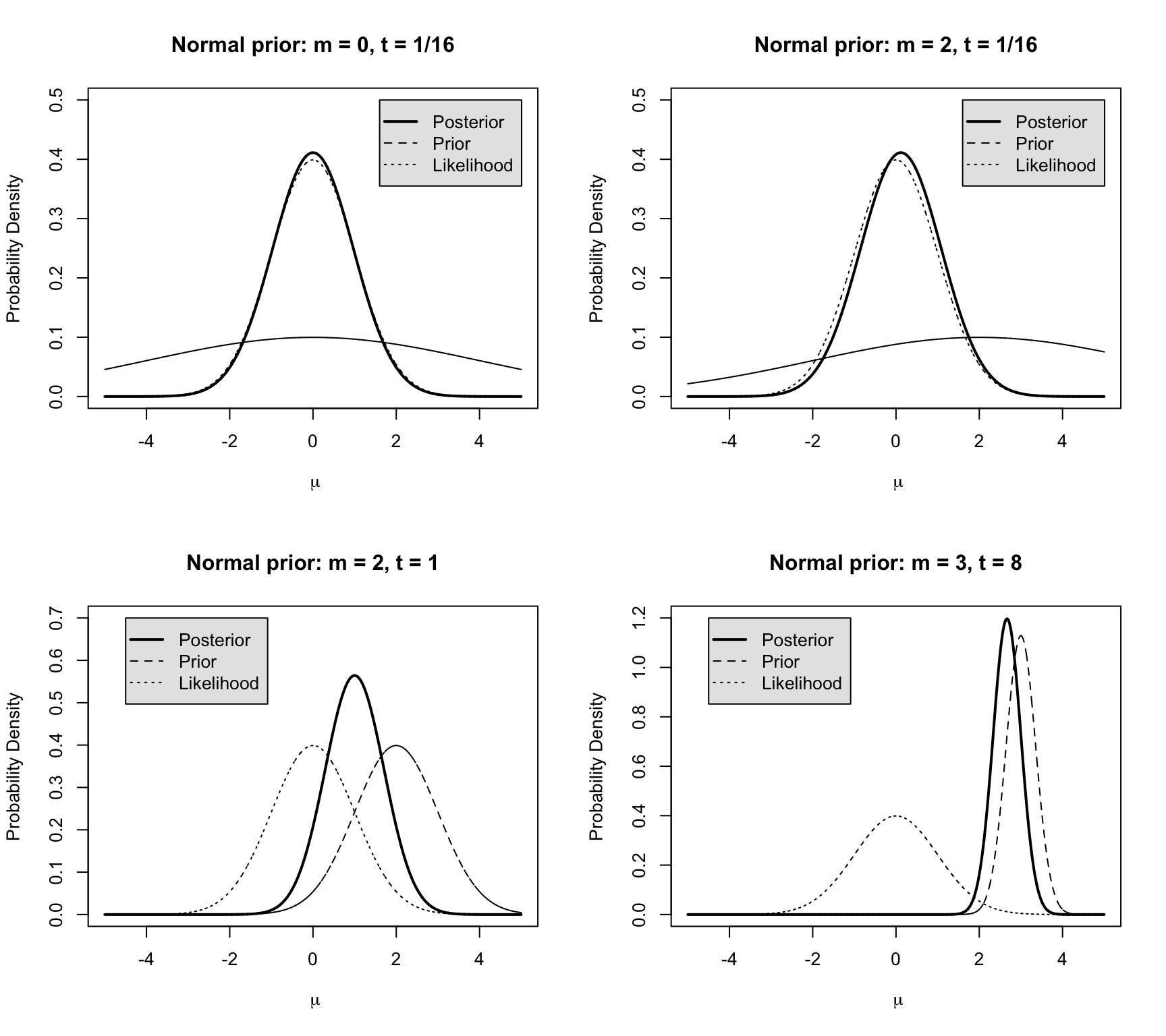
Posterior for the normal distribution, when likelihood is N(0,1) with four different priors

圖 43.1: Posterior for the normal distribution, when likelihood is N(0,1) with four different priors

43.2.1 \(n\) independent identically distributed observations

假設觀察數據爲:

\[ y_i, \cdots, y_n \stackrel{i.i.d}{\sim} N(\mu, \sigma^2 = \frac{1}{\tau}) \]

\(\tau\) 依然被定義爲精確度。那麼這組數據的均值的時候概率分布，可以有兩種計算手段:

  1. 利用公式 (43.1): 根據正態分布的性質 \(\bar{y} \sim N(\mu, \frac{\sigma^2}{n} = \frac{1}{n\tau})\)，我們可以直接計算均值的事後概率分布是均值爲 \(\frac{n\tau\bar{y} + \gamma\nu}{n\tau + \gamma}\)，精確度爲 \(n\tau + \gamma\) 的正態分布;
  2. 利用觀察數據推導:

\[ \begin{aligned} y_i, \cdots, y_n & \stackrel{i.i.d}{\sim} N(\mu, \sigma^2=\frac{1}{\tau}) \\ \Rightarrow \text{The likelihood: } & (\frac{\tau}{2\pi})^{\frac{n}{2}}\text{exp}\{ -\frac{\tau}{2}\sum_{i=1}^n(y_i - \mu)^2 \} \\ \because \sum_{i=1}^n(y_i - \mu)^2 & = \sum_{i=1}^n(y_i - \bar{y} + \bar{y} - \mu)^2 \\ & = \sum_{i=1}^n(y_i - \bar{y})^2 + n(\bar{y} - \mu)^2 \\ & = (n-1)s^2 + n(\bar{y} - \mu)^2 \\ \text{Where } s^2 & = \frac{(y_i - \bar{y})^2}{n-1} \\ \Rightarrow \text{The } & \text{likelihood become: } \\ & (\frac{\tau}{2\pi})^{\frac{n}{2}}\text{exp}\{ -\frac{\tau}{2}[(n-1)s^2 + n(\bar{y} - \mu)^2] \} \\ \text{Ignoring } & \text{terms without } \mu \\ & \text{exp} \{ -\frac{n\tau}{2}(\bar{y} - \mu)^2 \} \\ \Rightarrow \text{Posterior } & \text{mean distribution: }\\ & N\{ \frac{n\tau\bar{y} + \gamma\nu}{n\tau + \gamma}, \text{precision} = (n\tau + \gamma) \} \end{aligned} \]

43.3 事後預測分佈 Posterior predictive distribution

對於一個接下來將要被收集數據的預測，\(\tilde{y}\)。在已經有的數據的條件下，它的條件分佈是 \(p(\tilde{y} | y)\)。可以通過積分來運算：

\[ \begin{aligned} p(\tilde{y} | y) & = \int p(\tilde{y|}\theta) p(\theta | y) d\theta \\ & = \int \exp(-\frac{1}{2\sigma^2} (\tilde{y} - \theta)^2) \exp(-\frac{1}{2\tau_1^2}(\theta - \mu_1^2))d\theta \end{aligned} \]

其中，

  • \(\mu_1 = \frac{\frac{1}{\tau_0^2}\mu_0 + \frac{1}{\sigma^2}y}{\frac{1}{\tau_0^2} + \frac{1}{\sigma^2}}\)
  • \(\frac{1}{\tau_1^2} = \frac{1}{\tau_0^2} + \frac{1}{\sigma^2}\)

我們又可以根據公式 (42.3) 和 (42.4) 來進一步推導預測變量在已有的觀察數據的基礎上的均值和方差：

\[ \begin{aligned} E(\tilde{y}|y) & = E(E(\tilde{y}|\theta, y) | y) \\ \because & \tilde{y}\perp y \text{ new data is independent from the data collected} \\ & = E(E(\tilde{y}|\theta) | y) \\ \because & E(\tilde{y} | \theta) = \theta \\ & = E(\theta |y) = \mu_1 \end{aligned} \]

\[ \begin{aligned} \text{var}(\tilde{y} | y) & = E(\text{var}(\tilde{y}|\theta , y) | y) + \text{var}(E(\tilde{y | \theta, y}) | y) \\ & = E(\sigma^2 | y) + \text{var}(\theta | y) \\ & = \sigma^2 + \tau_1^2 \end{aligned} \]

也就是說我們希望預測的新數據的 \(\tilde{y}\) 的均值等於 \(\theta\) 的事後概率分佈的均值 \(\mu_1\)，方差則由兩部分構成，一是模型方差 \(\sigma^2\)，一是事後概率分佈的方差 \(\tau_1^2\)。

上述過程很容易被擴展到有多個獨立同分佈 (independent and identically distributed) 觀察變量 \(y = (y_1, \dots, y_n)\) 時的情況：

\[ \begin{aligned} p(\theta | y) & \propto p(\theta)p(y | \theta) \\ & = p(\theta) \prod_{i = 1}^n p(y_i | \theta) \\ & = \exp(-\frac{1}{2\tau_0^2} (\theta - \mu_0)^2)\prod_{i = 1}^n \exp(-\frac{1}{2\sigma^2}(y_i - \theta)^2) \\ & = \exp(-\frac{1}{2}(\frac{1}{\tau_0^2}(\theta - \mu_0)^2 + \frac{1}{\sigma^2}\prod_{i =1}^n(y_i - \theta)^2)) \end{aligned} \]

事實上根據獨立同分佈正（常）態分佈數據的特徵可知，事後概率分佈此時取決於這 \(n\) 個獨立同分佈樣本的均值 \(\bar{y} = \frac{1}{n}\sum y_i\) 本身。於是有 \(\bar{y} | \theta, \sigma^2 \sim N(\theta, \sigma^2/n)\)，此時把 \(\bar{y}\) 本身作為一個單一觀察變量的模型即可獲得：

\[ p(\theta | y_1, \dots, y_n) = p(\theta | \bar{y}) = N(\theta | \mu_n, \tau^2_n) \]

其中，

\[ \mu_n = \frac{\frac{1}{\tau_0^2}\mu_0 + \frac{n}{\sigma^2}\bar{y}}{\frac{1}{\tau_0^2} + \frac{n}{\sigma^2}} \text{ and } \frac{1}{\tau_n^2} = \frac{1}{\tau_0^2} + \frac{n}{\sigma^2} \]

References

De Finetti, Bruno. 1974. Theory of Probability: A Critical Introductory Treatment. Transl. By Antonio Machi and Adrian Smith. J. Wiley.
Smith, Adrian. 1995. “A Conversation with Dennis Lindley.” Statistical Science 10 (3): 305–19.

  1. Foreward for “Theory of probability, a critical introductory treatment” by B. de Finetti(Wiley, 1974)(De Finetti 1974); see also Smith (1995)(Smith 1995)↩︎