第 95 章 爲什麼我們要用貝葉斯統計學方法?
- Everybody is a Bayesian. It’s just that some know it, and some don’t.
- Trivellore Raghunathan
統計學模型 (理論),結合現實的數據 (實踐),才能讓我們深刻地理解這個世界,既能檢驗我們的理論,又能從中找出規律性,爲一些現象做出總結和結論。如果說這個理論和實踐相結合的過程有類別之分,那麼最大的兩個類別區分就是: 概率論,和貝葉斯理論。
試從一個醫生的角度來思考他推斷一個患者疾病的過程: 門診中,有個患者因爲身患多種症狀前來就醫,他/她自己可能認爲自己患了某種疾病。你作爲接診的醫生,在思考和推斷患者是否患有他/她所認爲的那種疾病時,你的思考會建立在如下的前提 (prior view) 之上: 你觀察到的患者症狀,患者的家族病史,會帶來相同症狀的不同疾病的鑑別診斷。接下來,你可能讓該患者去做一些具體的生理生化,影像或者病理學檢查 (收集相應的數據)。接下來,你收到了該患者的生理生化檢查結果,影像報告和病理學報告,在看了這些報告 (分析獲得的數據) 過後,你重新再對患者到底是否患上該種疾病進行評估,獲得你心中認可的,他/她患有該疾病的概率 (updates their prior in light of the data to get a posterior view on whether the patient has the disease)。當然,更加常見的情況是,你看了這些初步報告之後,可能又讓該患者進一步做一些確診性質的檢查,用於輔助診斷。可能你還沒意識到,這個思考過程,就是一個十分典型的貝葉斯方式的推理。
在上面的醫生給患者做診斷的例子中,醫生診斷的過程,其實就是在評估該特定患者患有某種疾病的概率。很顯然不同的醫生可能會給出不同的概率 (=不同的診斷),這個概率,其實是一個主觀概率 (subjectively)。每個醫生給出的概率大小,其實是他/她自己對於給定了相應的數據 (患者主訴,檢查報告) 之後對於該患者患有該疾病的可能性的度量。(The size of the probability represents the physician’s degree of belief about the occurence of an event, i.e. their own personal assessment of how likely an event is, based on the evidence available to them.) 這樣的主觀概率,你是否也認爲它比起概率論者常說的概率更加接近我們平時常說的 “概率” 的概念呢? (概率論者的”概率”: 一個事件發生的概率,等於在無數次相同的實驗中,該事件發生次數所佔的比例)。所以這個貝葉斯方式的主觀概率,其實是因人而異的 (其屬性在於人),而非所謂的客觀現象 (not the phenomenon of interest)。所以,主觀概率是貝葉斯統計學的最基礎思維方式。
下面我們用兩個例子,來闡述貝葉斯和概率論兩種統計學思維所展示的不同。第一個來自論文 (Johnson et al. 2009),該論文中,作者使用了貝葉斯統計方法重新分析了使用概率論方法分析過的一個臨牀隨機試驗的結果。第二個例子來自於 (Spiegelhalter, Abrams, and Myles 2004),叫做 GREAT 的隨機臨牀試驗。
95.1 氨甲喋呤 (methotrexate) 在系統性硬皮病 (systematic sclerosis, SSc) 中的療效
95.1.1 背景資料-SSc trial
某臨牀試驗 (RCT) 的設定是這樣的,兩組患者,一組是新療法 (氨甲喋呤),一組是安慰劑 (或者標準療法)。在一個傳統的概率論者的框架底下,分析這樣一個RCT試驗數據的人最有可能進行的分析步驟如下:
- 建立一個所謂的零假設 (歸零假設), null hypothesis: 氨甲喋呤對於系統性硬皮病的治療是無效的。
- 確定一個和零假設互補的替代假設。
- 設定 0.05 (或者 5%) 作爲假陽性出現概率,也就是 type I error。
- 通過模型計算,報告 p 值。
那麼,當報告中的 p 值 \(> 0.05\) 時,大多數蠢蠢欲動的醫生和研究者可能就會下結論說: “我們沒有找到足夠的證據來拒絕零假設”。事實真的是這樣子嗎?更糟糕的是,許多這樣的臨牀試驗可能會被打上 “negative (消極結果)” 的標籤,然後經過很多年以後大家都認爲這個RCT就被總結成了類似 “氨甲喋呤無效”,或者 “氨甲喋呤不能治療系統性硬皮病”等結論在醫學界被傳播。要知道,類似系統性硬皮病這樣的稀少疾病,其實是很難找到足夠的患者數量進行臨牀試驗的。這些稀少疾病的臨牀試驗中,p 值 \(> 0.05\) 很可能只是反映了獲得數據的統計效能不足 (lack of power),並不一定就說明了藥物或者療法是無效的。
系統性硬皮病是一種患病率極低的罕見疾病。目前沒有特效藥物治療該疾病,從而導致患者長期忍受疾病的折磨,生活品質因爲身體機能的下降而長期處在十分低下的水平。過去有兩個小型試驗報告了氨甲喋呤 (MTX) 可能在系統性硬皮病的治療中起到積極的效果,於是就有研究者組織了一個爲時一年的隨機雙盲臨牀試驗,對象是那些系統性硬皮病的早期患者。35名患者被隨機分配接受 MTX 治療,另外36名患者被分配至了安慰劑對照組。期間有一些患者中途退出了試驗,多數退出的患者的理由是,治療缺乏有效性。
MTX對系統性硬皮病的治療效果評價,使用了三個指標:
- modified Rodnan skin score (MRSS) - 得分範圍: 0-78;
- University of California Los Angeles (UCLA) skin score - 得分範圍 0-30;
- Physician global assessment of overall disease activity (ODA) - 使用視覺模擬指標,評分範圍從 0 (無疾病) 至 10 (極爲嚴重疾病) 不等。
95.1.2 概率論者分析結果
下圖 95.1 所示的表格,是從論文 (Johnson et al. 2009) 中節選出來的,該表格展示了典型的概率論者分析該臨牀試驗數據的結果,當時的分析中,只對最終完成試驗的患者的數據進行了分析。

圖 95.1: Methotrexate in Seleroderma: results of a frequentist analysis
根據這個分析結果,概率論者報告了下面三個 p 值:
- MRSS - 效果不顯著 (\(p \geqslant 0.05\));
- UCLA - 效果不顯著 (\(p \geqslant 0.05\));
- ODA - 有(概率論)統計學意義的顯著效果 (\(p = 0.04\))。
要知道,這個臨牀試驗,在設計的時候是計劃能夠通過它尋找 35% 或者以上的療效差異的。所以,任何小於 35% 的療效 (儘管在臨牀上很可能是有意義的) 在概率論的理論框架下都是無法被檢驗,或者沒有足夠的統計效能來檢驗的。於是概率論持有的研究者就此結果下了結論: 我們沒有找到足夠的證據來拒絕 “氨甲喋呤在治療系統性硬皮病上是無效的” 這一零假設。如此,過了一些時日,這個試驗的結論在醫學界漸漸就變成了 “氨甲喋呤不能治療系統性硬皮病”。
其實,概率論持有者下的結論,其真實的含義是: 如果,零假設 (“氨甲喋呤在治療系統性硬皮病上是無效的”) 是正確的,假如可以重複無數次相同的臨牀試驗 (每次都找來不同的各自獨立的系統性硬皮病早期患者),那麼我們能觀察到和該次RCT試驗得到的試驗療效相同,甚至療效更加顯著的試驗出現的概率是大於 0.05 的。你爲這樣的結論,真的正面回答了你想知道的問題了嗎?
我認爲,更加能夠回答大衆或患者們所關心的關於這個試驗的醫學問題應該是,“當我們獲得且分析了試驗數據以後,氨甲喋呤對於系統性硬皮病治療有效的概率是多少 (what is the probability that the intervention is effective given the data?)”。貝葉斯統計學其實可以讓我們正式地,在數學模型上把已知的對於某個事件的知識包括進試驗獲得的數據及其模型當中去,從而計算這個新的治療方法在考慮了已知的醫學背景,及現有的試驗數據之後,它對於疾病的治療是有效的概率到底是多少。這才應是每一個臨牀試驗真正想要回答的最關鍵的問題。
95.1.3 貝葉斯統計分析結果
使用貝葉斯統計理論分析相同臨牀試驗數據的結果,已經被發表在論文(Johnson et al. 2009)中,我們節選其總結的表格在下圖 95.2 中。在該表格中,可以看見作者除了對完成試驗的患者的數據進行分析,同時使用補全法補過缺失值後的數據分析結果也展示在 “imputing missing data” 這一列中。
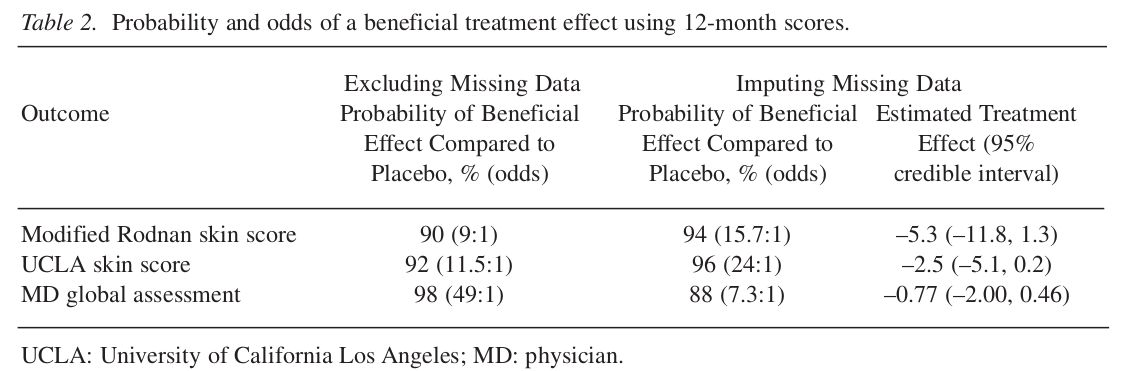
圖 95.2: Methotrexate in Seleroderma: results of a Bayesian analysis
貝葉斯統計分析的結果,直接且正面的回答了我們想知道的問題,那就是 MTX 到底對於治療系統性硬皮病這一疾病來說是不是有效的。從圖 95.2 中的表格,以及該論文中作者用貝葉斯多元模型分析的結果可以看到,貝葉斯模型推算的是 MTX 在使用三種不同指標進行療效評估時,MTX可以被認定爲有療效的概率。(Johnson et al. 2009)報告說,有96%的可能性,在使用三種療效評估方法中的兩種或者以上來評估時,我們講看到 MTX 其實是可以改善系統性硬皮病的病情的 (也就是有效的)。
圖 95.2 中表格用的先驗概率是不明確的,沒有太多信息的先驗概率 (vague/flat prior),其含義是:
- 所有可能的治療效果,不論大小,都被認爲有相似的先驗概率 (prior)。(every possible size of treatment effect considered equally likely a priori)
- 沒有太多信息的先驗概率意味着不提供太多的背景知識給模型。(no external information to current trial incorporated in analysis)
但是,其實我們是有背景知識的,在做這個臨牀試驗之前,已經有兩個小型試驗告訴人們, MTX很有可能可以治療系統性硬皮病,這才導致研究者組織了這第三次臨牀試驗。這兩個小型試驗的結果,被 (Johnson et al. 2009) 巧妙地轉換成爲含有信息的先驗概率 (informative prior)。
圖 95.3 展示的是,使用兩種先驗概率所計算的不同的後驗概率的結果之比較。左邊使用的是沒有信息的先驗概率 (flat, wide black prior distribution),右邊則使用的是有信息的先驗概率。兩個圖中,黑色線均爲先驗概率,綠色線是似然 (來自本次實驗的數據),紅色線是後驗概率。紅色的面積表示 MTX 在MRSS療效指標中支持其有效的概率,95%CrI是各自的可信區間。可見,當只使用來自本次試驗的數據的時候 (無信息的先驗概率,左邊圖),療效的點估計,和可信區間,是十分接近概率論者計算的點估計和信賴區間的。與之相對的是,當我們給模型中加入了有信息的先驗概率分佈時,後驗概率分佈給出的點估計和可信區間發生了變化:
- 後驗概率分佈向右邊 (治療無效) 發生了位移 (shift towards no treatment effect),也就是療效的點估計從 -5.3 下降至 -3.4;
- 95%可信區間的範圍變得比左邊使用無信息先驗概率的結果狹窄了 (估計變得精確了),從之前的 (-11.8, 1.3) 變窄至 (-7.3, 0.4)。
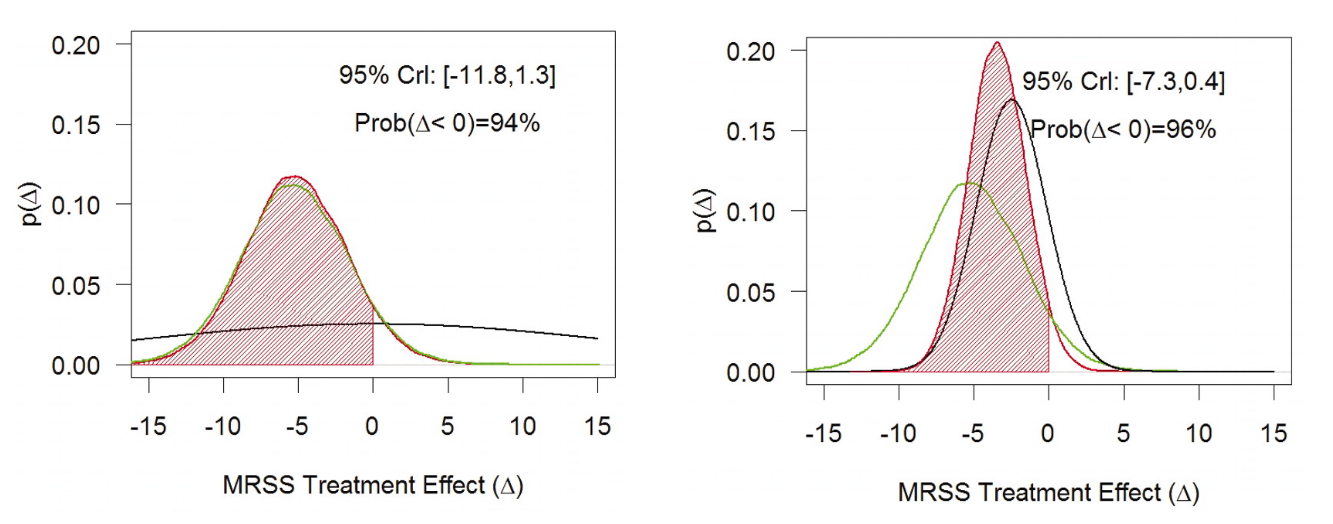
圖 95.3: Methotrexate in Seleroderma: comparison of priors
紅色面積 (也就是支持 MTX 治療有效的概率),因爲分佈的位移,以及可信區間變窄的原因,從 94% 略增加到了 96%。
在這個實驗中先驗概率分佈和該次試驗計算的似然給模型提供了相似的信息量。在更多的情況下,歷史數據,背景知識只能給出有限的信息量。所以,一個使用貝葉斯方法計算的統計報告,你會看見統計學家使用多個不同的先驗概率分佈,加上該次試驗的似然,來計算多個不同先驗概率下給出的後驗概率分佈結果,從而展示他/她給出的結論對於不同先驗概率的敏感程度。
這個實例給我們展示了貝葉斯統計學能做到,而概率論統計學不能做到的幾個要點:
- 貝葉斯分析結果可以告訴我們,藥物有效的概率是多少,簡單直接了當。
- 背景知識,除了你可以洋洋灑灑地寫在論文中之外,竟然還可以被當做一種先驗概率分佈,有效地和實驗數據獲得的似然相結合,妙哉妙哉。
- 三種評估手段,可以通過貝葉斯統計學模型整合到一起,同時給出後驗概率的分佈,這在傳統的概率論統計學模型中是很難,甚至是不可能做到的。貝葉斯方法同時還允許我們建立十分複雜的模型,且不必擔心模型擬合計算量對電腦的要求。
- 中途退出試驗的患者數據可以使用貝葉斯方法簡單地歸納進統計模型中來,概率論統計學所使用的缺失值的補全法其實相比貝葉斯法來說顯得不完整,且可靠程度較低。
- 醫生從貝葉斯統計方法計算的結果中獲得了更加多的信息,和結論。你可以計算超過某個療效差異的概率大小。在貝葉斯統計學方法中,整個事後概率的密度分佈圖都可以給出,而不僅僅是一個點和信賴區間的估計。
95.2 Example: The GREAT trial
接下來我們一起一步一步利用GREAT臨牀試驗數據,看看下面不同的分析方法會帶給我們什麼樣子的結果:
- 經典統計學方法;
- 貝葉斯統計學方法(通過兩種不同的先驗概率分布)
95.2.1 Background (GREAT trial)
GREAT 臨牀試驗是一項隨機雙盲對照試驗(RCT),試驗藥物是阿尼普酶(anistreplase,復合纖維溶解酶),具有溶解血栓的效果。該試驗比較的是傳統的心肌梗塞(myocardial infarction, MI)被確診之後的治療方法,和家庭醫生對患者確診心肌梗塞之後在家中就立即服用阿尼普酶的療效是否有差異。
- 主要結果:30天死亡率
- 之前有過研究(GISSI trial),結果表明,當患者在醫院時,阿尼普酶如果在確認患者發生心肌梗塞之後一小時內服用,能夠有效降低患者因心肌梗塞導致的一年死亡率 (從19%降低至12%)。但是當投藥發生在患者心肌梗塞確診6小時以上時,死亡率則沒有變化。
- 本次試驗的方法是:
- 家庭醫生給予患者阿尼普酶 (治療組) 或者安慰劑 (對照組);
- 當患者被送至醫院後,院內給予安慰劑(治療組),或者阿尼普酶 (對照組)。[注意二者投藥順序正好相反]。
95.2.3 經典統計學分析方法
觀察數據給出的比值比的點估計可以計算爲: \(\text{OR} = \frac{13/(163-13)}{23/(148-23)} = 0.47\); 根據比值比的對數服從正態分布,且標準誤爲: \(\text{SE}_{\log(\text{OR})} = \sqrt{\frac{1}{13} + \frac{1}{163-13} + \frac{1}{23} + \frac{1}{148-23}} = -0.7528664\),那麼 \(\log{\text{OR}}\) 的95%CI 可以計算爲\(\log{0.47} \pm 1.96*(-0.7528664) = (-1.47, -0.03)\),再反過來計算\(\text{OR}\)的95%CI,可以獲得比值比的信賴區間是:\((0.23, 0.97)\)。
至此,傳統的統計學方法的計算過程結束,獲得點估計: \(\text{OR} = 0.47; 95\%\text{CI:} (0.23, 0.97), p = 0.04\)。
95.2.4 貝葉斯統計學分析方法
- 先驗概率使用專家意見: expert prior
- 專家的意見來自之前已經進行過的三個較小的臨牀試驗:
- 阿尼普酶可能可以降低一些死亡率,但是不多 (15-25%);
- 阿尼普酶不太可能降低死亡率達到40%或者以上
- 這個專家意見被貝葉斯統計學家用統計學語言翻譯成: 在比值比尺度上(OR),治療組(家中立即服用阿尼普酶)相對對照組的比值比的95%信賴區間應該在 \((0.6, 1)\) 範圍內,包括1。
- 我們還需要把這句話再進行對數轉換以便於做邏輯回歸計算 (log-odds ratio)
- \(\log(\text{OR})\) 的95%信賴區間的範圍需要落在\((-0.51, 0)\)之內;
- 這相當於就是一個均值爲 \(\log(0.6)/2 = -0.26\), 方差是 \((\frac{0-\log(0.6)}{2} = 0.13)^2\) ,的正態分布:
x <- seq(0, 1.5, by = 0.001)
y <- dlnorm(x, meanlog = -0.26, sdlog = 0.13) # use log Normal Distribution generator
plot(x, y, type = "l", frame = F, #ylab = "lognormal(-0.26, 0.13)",
ylim = c(0, 4.5), yaxt='n', ylab = "",
xlab = "Odds ratio", main = "lognormal(-0.26, 0.13)")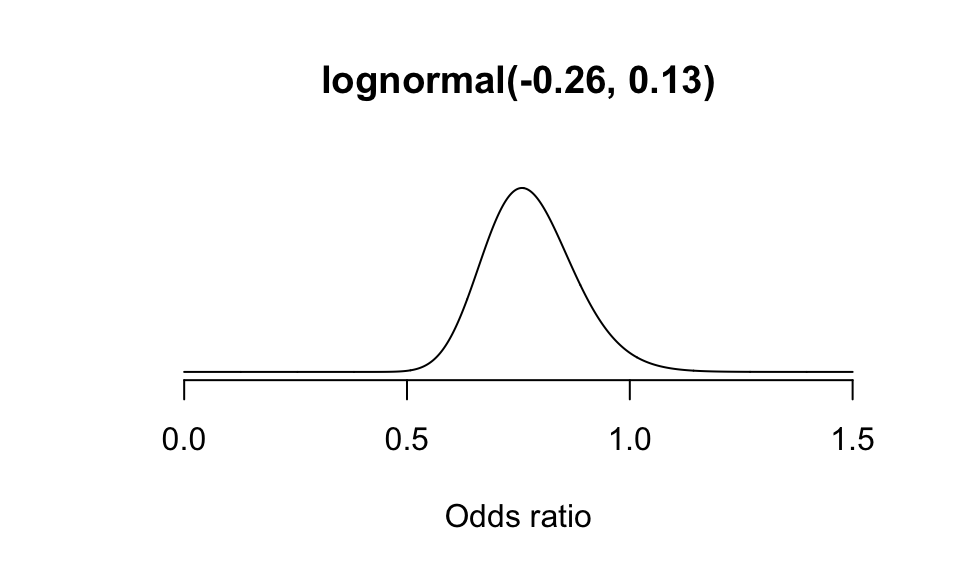
圖 95.4: Expert Prior probablity density: small reductions in mortality likely, no or large benefit unlikely.
- 但是GREAT臨牀試驗的數據告訴我們,\(\text{OR} = 0.47; 95\%\text{CI:} (0.23, 0.97), p = 0.04\),它的分布是數據支持的似然函數分布:
x <- seq(0, 1.5, by = 0.001)
y <- dlnorm(x, meanlog = -0.26, sdlog = 0.13) # use log Normal Distribution generator
z <- dlnorm(x, meanlog = log(0.47), sdlog = (-0.03+1.47)/(2*1.96))
plot(x, y, type = "l", frame = F, #ylab = "lognormal(-0.26, 0.13)",
ylim = c(0, 4.5), yaxt='n', ylab = "",
xlab = "Odds ratio", main = " ")
points (x, z, type="l", col="blue")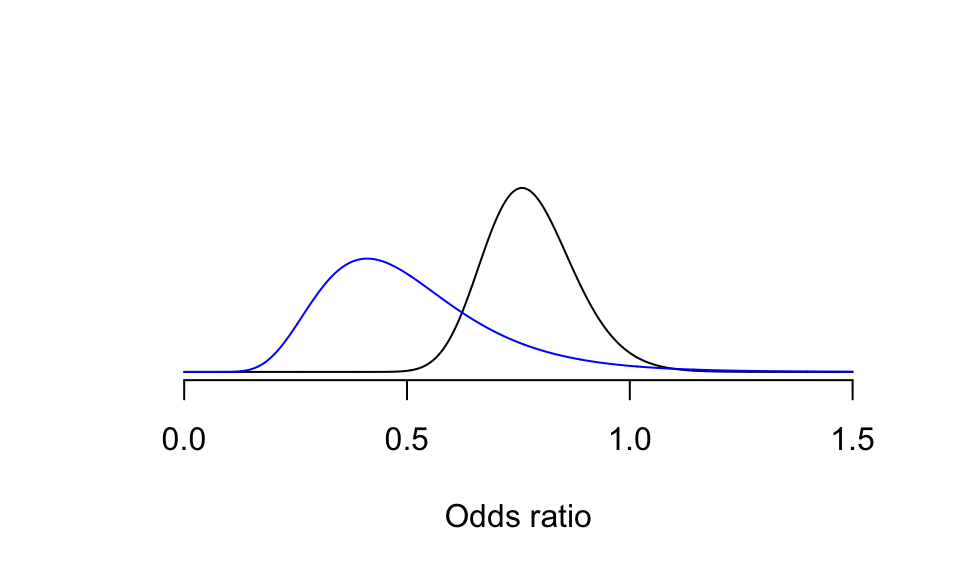
圖 95.5: Expert Prior probablity density: small reductions in mortality likely, no or large benefit unlikely, adding likelihood (blue) from the GREAT trial.
- 當我們使用貝葉斯方法把專家給出的先驗概率,以及本次實驗給出的似然合並之後,獲得的事後概率認爲,心肌梗塞患者在家中立刻服藥沒有幫助或者甚至有害的概率是0.5%:
x <- seq(0, 1.5, by = 0.001)
y <- dlnorm(x, meanlog = -0.26, sdlog = 0.13) # use log Normal Distribution generator
z <- dlnorm(x, meanlog = log(0.47), sdlog = (-0.03+1.47)/(2*1.96))
u <- dlnorm(x, meanlog = -0.3, sdlog = 0.12)
plot(x, y, type = "l", frame = F, #ylab = "lognormal(-0.26, 0.13)",
ylim = c(0, 4.5), yaxt='n', ylab = "",
xlab = "Odds ratio", main = " ")
points (x, z, type="l", col="blue")
points(x, u, type = "l", col = "red")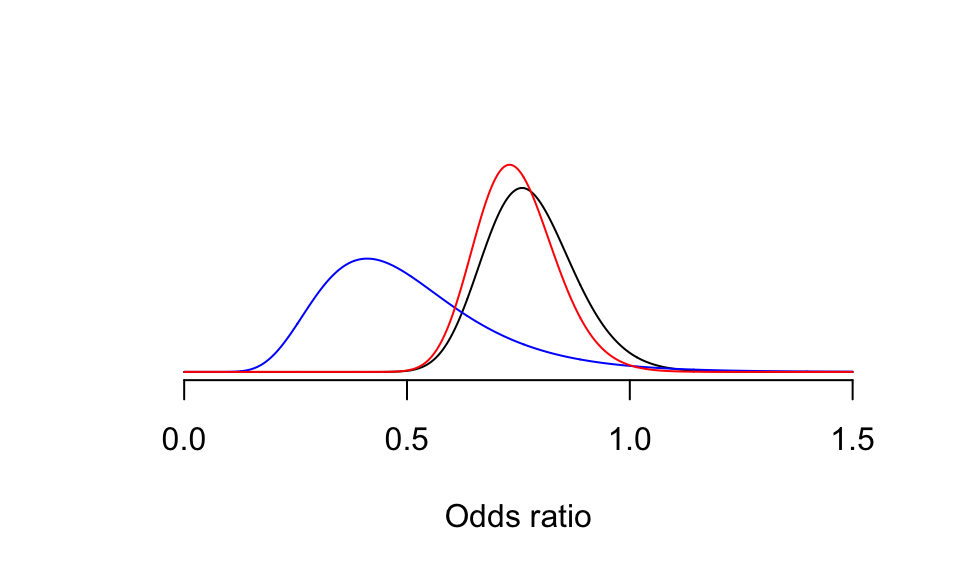
圖 95.6: Expert Prior probablity density: small reductions in mortality likely, no or large benefit unlikely, adding likelihood (blue) from the GREAT trial, and posterior distribution (red).
- 先驗概率使用懷疑觀點的概率分布: sceptical prior
- 假定我們不相信專家意見,懷疑地認爲阿尼普酶對降低心肌梗塞患者死亡率本身應該沒有什麼效果的話,可以認爲比值比爲1,也就是 \(\log(\text{OR}) = 0\)。同時還認爲有顯著療效是小概率事件。此時,先驗概率的分布可以表示爲:
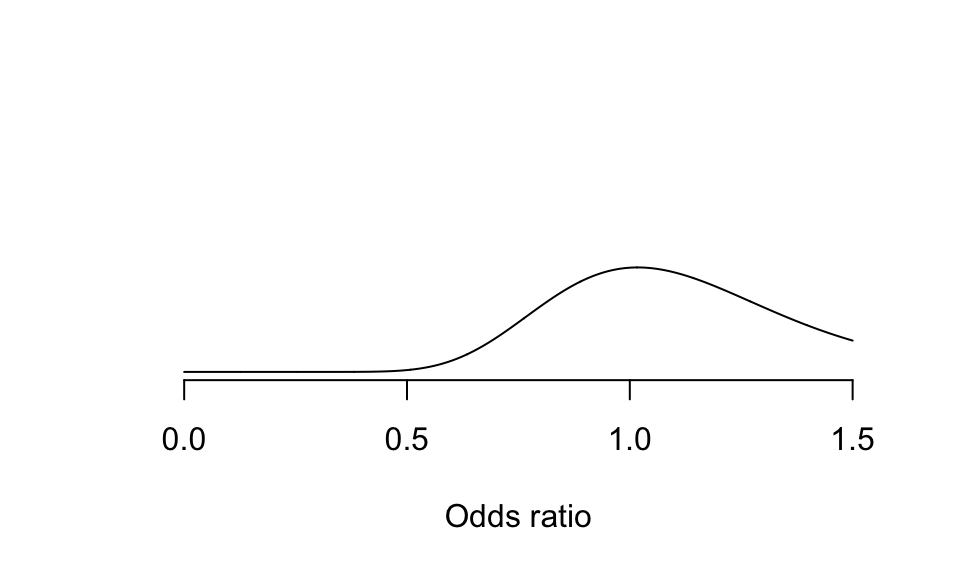
圖 95.7: Sceptical Prior probablity density, no benifit or large treatment effect unlikely
- 即便如此,實驗數據給出的似然函數分布依然把這個持懷疑觀點的先驗概率分布向治療有效的方向拉動了,此時給出的心肌梗塞患者在家中立刻服藥沒有幫助或者甚至有害的概率是8%:
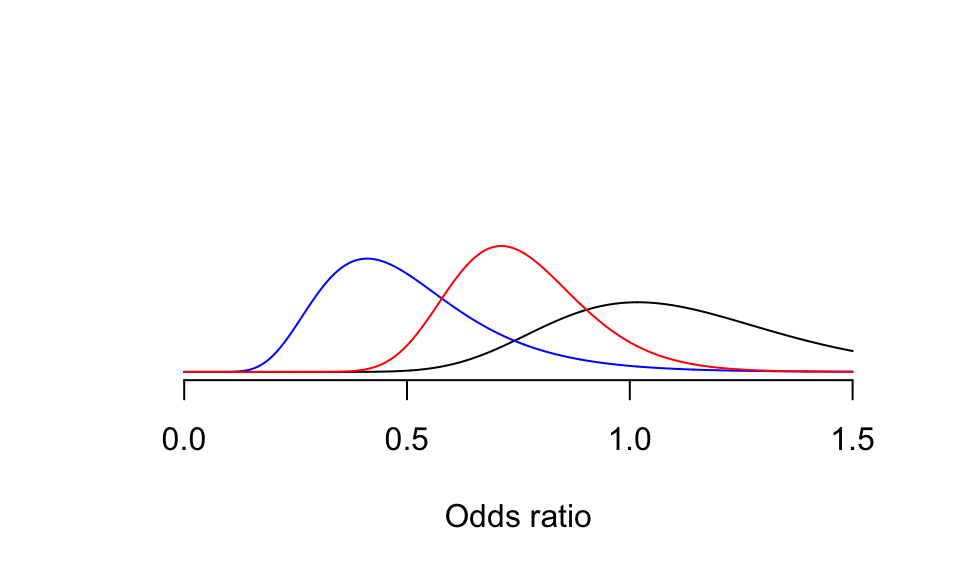
圖 95.8: Sceptical Prior probablity density, adding likelihood (blue) from the GREAT trial, and posterior distribution (red).
專家的觀點十分樂觀,但是它仍然起到了把實驗數據給出的似然概率向更現實的方向(不那麼樂觀的方向)拉動了一點點,使用專家意見給出的事後比值比均值是0.73,值得關注的是,採用懷疑論觀點的先驗概率分布,也能給出相似的事後比值比均值 0.70,只是懷疑觀點的先驗概率分布使得事後概率分布中藥物可能無效甚至有害的概率變大了。這個分析展示了,一個對該藥物療效持懷疑觀點的人,和持樂觀觀點的人二者分析相同數據時很可能作出不同的結論,但是有一點是相同的,那就是傳統概率論統計學計算獲得的比值比,\(\text{OR} = 0.47; 95\%\text{CI:} (0.23, 0.97), p = 0.04\)不論與專家意見相比,還是和懷疑論者相比,都過於樂觀了 (0.48 is too good to be true)。