第 89 章 分析策略和模型檢查 Model checking-survival analysis

89.1 本章概要

  • 學會如何有計劃，步驟清晰地對生存數據進行比例風險模型的建模，包括如何恰當地選擇放入模型中的解釋變量，和它們的形式。
  • 能進行模型與模型之間比較的似然比檢驗 (likelihood ratio test)，並解釋該檢驗的結果。
  • 掌握各種不同的檢驗“比例風險假設”的方法，特別是使用 Schoenfeld 殘差圖的方法，來觀察暴露變量對風險函數的作用是否隨着時間發生改變。
  • 使用 Martingale 殘差圖和偏差殘差圖 (deviance residuals) 評價模型擬合程度 (model fitting)。
  • 使用 Martingale 殘差來輔助判斷某個連續型變量合適放入模型的數學函數形式。
  • 會使用 R/Stata 獲取風險比例模型建立之後的各種不同殘差。

89.2 生存分析策略

在分析生存數據的時候同樣一個數據集，你其實可以建立許多不同的（比例風險）模型，那麼解釋變量的選擇就顯得很重要，究竟你應該在模型中放入哪些變量才算是合適呢？其實這要根據研究的目的和分析時的上下文而有相應的調整。例如說，

  1. 分析目的只是着重看某個暴露變量對生存/死亡風險的影響。也就是我們說到底只關心一個特殊的暴露變量。但是我們希望這個模型可以調整其他可能存在的混雜因子，從而獲得該暴露變量真實的效果 (true effect)。
  2. 分析目的是爲了瞭解測量獲得的一組暴露變量數據集與研究對象生存時間之間的關係。其中可能着重關心該變量集合中的一個或者幾個對生存的影響，或者最終決定哪個/些是對生存概率的影響較大的。
  3. 分析目的是爲了建立一個預測生存概率的模型。研究者可能希望通過在模型中加入儘可能多的變量以提高模型預測能力的精確度。這樣新的研究對象的生存概率就可以通過建立好的模型直接套用該對象具有的解釋變量計算。

在廣義線性回歸模型部分的分析策略章節 (Chapter 65) 詳細討論過一般分析數據時建立回歸模型的策略。該策略也可以用於指導生存分析模型建立的過程。

89.2.1 關於似然比檢驗 A note on likelihood ratio tests

似然比檢驗法同樣可以用於比較兩個具有嵌套結構的Cox比例風險模型。這裏用兩個簡單的解釋變量 \(X_1, X_2\) 來示範似然比檢驗的過程。

假設，我們主要對 \(X_1\) 和生存概率之間的關係感興趣，而 \(X_2\) 作爲唯一的混雜因子變量。那麼我們可以分別建立兩個生存分析模型，一個有 \(X_2\)，另一個不包含 \(X_2\)。如果這兩個模型給出的變量 \(X_1\) 的風險度比估計值發生了較爲顯著的變化，那麼可以考慮模型中要保留 \(X_2\) 作爲重要的混雜因子變量。如果包含了 \(X_2\) 的回歸模型給出的 \(X_1\) 的風險度比和不包含 \(X_2\) 的回歸模型給出的風險度比估計值差別可以忽略不計，且可以認爲 \(X_2\) 不是重要的獨立解釋變量，那麼我們決定把它從模型中移出也沒有太大的問題。如果數據集中有許多個潛在的混雜因子變量，那麼我們可以對每一個重複上述相同的步驟。最主要的是，要記住，對於混雜是否有意義，並沒有正式的檢驗方法。

如果 Model 1 包含的變量少於 Model 2 (Model 1 is nested within Model 2)，那麼似然比檢驗的檢驗統計量是

\[ -2 (\ell_{\text{Model 1}} - \ell_{\text{Model 2}}) \sim \chi^2_p \]

其中，

  • \(\ell\) 是表示兩個模型的對數似然 (log-likelihood)
  • \(p\) 是兩個模型中相差的預測變量的個數 (the difference in the number of parameters in the two models)。
  • 另外，這裏模型中還允許考慮變量之間的交互作用項或者是給連續型變量進行數學形式的調整（增加二次項甚至是三次，多次項）。

要注意的是，似然比檢驗顯然無法用於比較一個全參數模型（如 Weibull Model）和一個半參數模型（如 Cox 比例風險模型）。這是因爲他們之間不存在嵌套結構關係。

89.3 針對不同的研究設計不同的分析策略

分析策略需要根據不同的研究設計量身定製，下面我們着重討論兩種主要類型的生存數據研究設計 – 隨機對照臨牀試驗型 (randomised controlled trial, RCT)，和觀察性研究 (observational study)。

89.3.1 針對隨機對照臨牀試驗 RCT

思考一個有治療組和對照組的隨機對照臨牀試驗，例如目前位置我們一直使用的白血病患者數據。由於隨機分配的法則，使我們認爲除了治療本身的暴露，不存在其餘的組間差異。那麼我們認爲一個比較合理的分析策略應該可以歸納如下：

  1. 先總結 (summarize) 兩個不同治療組患者（實驗對象）的各方面數據：人數 (n)，事件數 (n of events)，刪失值數 (n of censors)，各組的生存時間中位數 (median of survival time)，及刪失對象的觀察時間長度的中位數 (median of censoring time)。
  2. 使用非參數法，繪製兩個治療組的 Kaplan-Meier 生存曲線。
  3. 再使用非參數法，特別是 log-rank 檢驗法對零假設：兩組生存曲線的模式無不同 (the survivor curves in the two treatment groups are the same)。
  4. 使用繪圖法，初步（非正式地 informally）判斷比例風險假設是否成立，或者可能被違反
  5. 如果可以認爲比例風險假設得到滿足，那麼，接下來可以進一步使用比例風險模型，或者你可能喜歡的指數模型，Weibull 模型等其他你認爲可能合適的模型來建立回歸模型，通過你最喜歡的R分析並計算獲得相應的風險度比 (hazard ratio) 及其信賴區間的估計。
  6. 最後，對該模型的風險比例假設進行正式的統計學評估（將在接下來的章節中詳述）。可以是使用治療組 \(\times\) 時間 這樣一個交互項看其回歸係數是否顯著不等於零，也可以是使用 Schoenfeld 殘差分析圖，也可以是把觀察時間進一步分割成幾個時間段之後分別估計每個時間段內的風險度比是否存在較大差異。

89.3.2 針對觀察型研究 observational studies

在觀察型研究獲得的生存數據中，分析者通常需要考慮多個不同類型的暴露（解釋變量）。同樣地，變量的選擇也要基於分析的目的和研究本身的設計來決定。同樣是觀察型研究，不同研究者的研究興趣各不相同。

  1. 某些觀察型研究的主要目的是估計某一個特別感興趣的暴露變量對生存概率的影響，但同時希望把可能對暴露和結果之間的關係造成混雜影響的因素都儘可能的控制住。
  2. 某些觀察型研究的主要目的是分析某幾個特定的暴露變量和生存概率之間的關係，同時希望瞭解哪些（個）變量可能對生存概率（時間）有最大的作用。
  3. 某些觀察型研究的主要目的是通過收集到的所有可能的解釋變量建立符合該實驗目的的生存概率預測模型，用於對患者/實驗對象的實際生存時間或者某個時間點的生存概率的估計。

先看第一種情況下的分析策略：

89.3.2.1 Type 1: 分析某個暴露變量對生存的影響 estimating an exposure effect

下列分析步驟僅僅只是一個大致的範圍和框架，供參考和討論：

  1. 第一步，先實施非參數法分析，對數據進行大致的瞭解：這不僅僅是生存分析過程中重要的開始步驟，也是所有生物統計分析開始的敲門磚和基石。
    • 對於可操作的變量（二進制型，多類別型）逐一繪製 Kaplan-Meier 生存曲線圖，實施 log-rank 檢驗。
    • 對每一個變量實施初步的比例風險前提的圖形觀察和評估。
    • 使用表格歸納法，或者是廣義線性回歸模型分析暴露變量之間可能存在的關係。
  2. 第二步，主要的建模分析：如果確認比例風險前提可以得到滿足，則多數研究者會選用比例風險模型（Cox半參數或者全參數模型），有時候取決於個人偏好。
    1. 建立最簡單的只有一個主要暴露變量的初步風險回歸模型 (Model 0)。
    2. 建立一系列的風險回歸模型，每個模型中的解釋變量除了前一步中的主要暴露變量意外，只單獨增加數據集中的一個變量。(fit further models including the main exposure and each potential confounder, one at a time)
    3. 觀察前一步中建立的系列風險回歸模型給出的主要暴露變量的風險度比估計（也就是主要暴露變量和生存概率之間的關係），主要留意哪些模型給出的估計和初步模型 Model 0 給出的風險度比估計相比變化顯著。(examine the impact of adjustment for each confounder on the estimated association between the main exposure and time-to-event, i.e. on the hazard ratio.)
    4. 使用交互作用項檢驗每一個變量和主要暴露變臉之間是否存在顯著的交互作用關係 (i.e. whether there are any interactions.)
    5. 選 iii. 步中判定是混雜因子的變量，如果 iv. 中發現有意義的交互作用關係也在這裏保留，建立一個略複雜的風險比例回歸模型 (Model 1)
    6. 第 v. 步中未加入 Model 1 的變量此時再逐步加入模型中來，說不定他們會是你在 v. 中選入作爲混雜因子變量之後的混雜因子 (confounders in the presence of other variables)
    7. 建立最終模型 (Model 2)，把 v. 和 vi. 中認爲需要調整的變量及可能存在的交互作用都加入進來。
  3. 第三步，檢查比例風險模型在上述各模型中是否都得到滿足。

89.3.2.2 Type 2: 分析某幾個特定的暴露變量和生存概率之間的關係 understand the associations between a set of several variables and the time-to-event

這其實是相對偏探索型分析的情境。之所以是這樣的分析目的，很大可能是我們並不太瞭解，或者這些暴露變量對該生存事件本身的影響沒有太多的背景知識，或者研究對象本身是來自相對未知的人羣，我們他們身上發生的（生存/疾病/死亡）事件本身比較沒有概念。所以在這樣的情況下，我們並不確定，也沒有把握哪個或者哪些變量對我們關心的事件發生之間可能有怎樣的關係。此時，如果你的數據集中收集的變量個數不多，很多研究者可能選擇使用減法的方法來篩選變量，也就是一開始就把所有的變量都放入模型中去。如此可以一開始就看到多個變量同時互相調整時對事件發生，生存概率的影響。相反，你也可以考慮使用我們在第一種情境（Type 1）下的步驟的擴展版：

  1. 第一步，先實施非參數法分析：
    • 對於可操作的變量（二進制型，多類別型）逐一繪製 Kaplan-Meier 生存曲線圖，實施 log-rank 檢驗。
    • 對每一個變量實施初步的比例風險前提的圖形觀察和評估。
    • 使用表格歸納法，或者是廣義線性回歸模型分析暴露變量之間可能存在的關係。
  2. 第二步，主要的建模分析：這一步其實有多種可能性，下面所寫的分析策略也只是多種可能的方案之一，僅作參考。
    1. 把每一個可能的變量，我們都先把它當作潛在的最重要的主要暴露變量，逐一建立只有一個解釋變量的風險比例模型。用似然比檢驗法，確認哪些變量對事件發生，或者生存概率之間的有單獨的有意義的關係。(assess whether each is associated with survival by itself using a likelihood ratio test)
    2. 把第 i. 步中確認單獨和生存概率有關係的變量全部放入一個風險比例模型。此時再使用似然比檢驗法，逐一篩選此時模型中的變量，看是否對模型的對數似然 (log-likelihood) 有顯著的影響，無則棄，有則留，最終保留的模型爲 Model 1。
    3. 第 ii. 步中丟棄的那些變量，我們在這一步中，再逐一放入 Model 1，看哪一個，或者有哪些在此時可能對模型的對數似然有顯著貢獻（還是使用似然比檢驗法），如果有，再把它（們）加回模型中去 (Model 2)。
    4. 最終確認 Model 2 中的變量沒有任何一個是可以再被從模型中移出的，確保每一個保留下的變量都對事件的發生有影響形成模型 Model 3。
  3. 第三步，檢查比例風險模型在上述各模型中是否都得到滿足。

89.3.2.3 Type 3: 建立預測模型

如果研究的目的是建立一個可靠的預測模型，我們可以使用和 Type 2 情境下相似的策略。不過如果你的數據集測量的非常多的變量，那麼你可能需要考慮在建立生存模型之前，進行一些數據的降維過程，提煉一些數據中真正需要的變量。

Example 89.1 另一個白血病患者的觀察數據，分析患者的白細胞計數，白細胞的某種特性 AG (+/-)，以及死亡時間之間可能存在的關係，這個數據包含了 33 名白血病患者的血液數據。數據中有兩個變量：

  • AG: 爲 0/1 的二進制變量 (0 = -; 1 = +)，它表示白細胞的某種特性 (characteristic)；
  • 白細胞計數 (WBC)：是一個連續型變量表示患者採集血樣中的白細胞的個數。

患者的生存時間的單位是“週”，範圍是 1 至 156 週，且該數據中 33 名患者最終都死亡了。（即，沒有刪失值） 下面的表格總結了該數據擬合的三個 Cox 比例風險回歸模型估計的各變量的風險度比，95%信賴區間，和模型的對數似然：

  1. 有且僅有 AG 一個解釋變量
  2. 有且僅有 WBC 一個解釋變量
  3. 有 AG, WBC 兩個解釋變量
AG WBC log-likelihood
Model (1) 0.307 (0.136,0.696) - -80.93
p = 0.005
Model (2) - 1.010 (1.001,1.020) -83.16
p = 0.038
Model (3) 0.336 (0.146,0.776) 1.008 (0.998,1.018) -79.79
p = 0.011 p = 0.117

你會選擇哪個模型？

# p value for likelihood ratio test comparing Model (3) with Model (1)
pchisq(-2*(-80.93 - (-79.79)), df = 1, lower.tail = FALSE)
## [1] 0.13105187
# p value for likelihood ratio test comparing Model (3) with Model (2)
pchisq(-2*(-83.16 - (-79.79)), df = 1, lower.tail = FALSE)
## [1] 0.0094274625

89.4 模型檢查的要點

建立風險比例模型之後，報告你的分析結果之前，我們應該實施的重要步驟還有模型的檢查。這一步保證了我們報告的結果可靠，且不至於給出錯誤的結論。生存數據模型的檢查，比起線性回歸模型要複雜一些，但是離不開下面三個要點：

  1. 總體模型對數據的擬合情況是否合理？(how good is the overall fit of the model?)
  2. 是否有極端數據，影響了模型的擬合結果？(Are there some individuals for whom the model does not provide a good fit?)
  3. 解釋變量，特別是連續型變量是否以正確的形式進入了模型？(Is the functional form for the explanatory variables correct?)

89.5 比例風險假設的檢查 check the proportional hazard assumtion

主要有三板斧：

  1. 用非參數法繪製簡單的生存曲線圖；
  2. 用統計檢驗，判斷一個解釋變量對風險的影響是否和時間產生了交互作用；
  3. 殘差繪圖法。

非參數法繪製生存曲線圖詳見第 86 章節部分。

89.5.1 比例風險檢查的統計檢驗法

在滿足比例風險前提下，某個解釋變量估計的風險度比 (hazard ratio) 不會隨著時間變化而變化，根據這個特點，我們可以認為，如果某些解釋變量在追踪開始時對風險影響很強，在之後的追踪中，和風險之間的關係變弱的話，(或者反過來)，那麼風險比的這一變化就違背了比例風險這一前提。最簡單的，我們可以在模型中加入該變量和時間的相乘項 (交互作用項)：

\[ h(t|x) = h_0(t)\exp\{ \beta x + \gamma (x\times t)\} \]

聰明的你一下子就明白了，接下來只要檢驗 \(H_0: \gamma = 0\):

\[ \frac{\hat\gamma}{SE(\hat\gamma)} \sim N(0,1) \]

89.5.2 用 Schoenfeld 殘差繪圖

另外一種視覺化檢查比例風險假設的方法是使用 Schoenfeld 殘差：

首先我們用下面的式子表示 Cox 風險比例模型的對數偏似然：

\[ \ell_p = \sum_j \beta^T x_{i_j} - \sum_j \log (\sum_{k \in R_j }\exp(\beta^T) x_k) \]

其中，

  • \(x_k\) 表示第 \(k\) 名對象的解釋變量組成的向量 \(x_k = (x_{1k}, x_{2k}, \dots, x_{pk})^T\)。
  • \(\beta\) 是每個解釋變量對應的回歸係數，也就是對數似然比估計 log-hazard ratios \(\beta = (\beta_1, \dots, \beta_p)^T\)
  • 偏似然是把所有事件發生的時刻時的條件概率相加起來。

該偏似然計算式取 \(\beta_1\) 的一階導數 (first derivative of \(\ell_p\) with respect to \(\beta_1\)) 是：

\[ \frac{d\ell_p}{d\beta_1} = \sum_j x_{1i_j} - \sum_j \frac{\sum_{k \in R_j} x_{1k} \exp\beta^T x_k}{\sum_{k \in R_j} \exp \beta^T x_k} \]

那麼在事件時間 \(t_j\) 時，我們定義 Schoenfeld 殘差 \(r_{s_{1j}}\) 爲：

\[ r_{s_{1j}} = x_{1i_j} - \frac{\sum_{k \in R_j} x_{1k} \exp\hat\beta^T x_k}{\sum_{k \in R_j} \exp \hat\beta^T x_k} \]

由於我們知道 \(\hat\beta\) 是當且僅當偏似然的一階導數等於零的情況下的極大似然估計。所以這些 Schoenfeld 殘差之和必須也爲零。這個殘差的涵義其實質是在比較每個事件發生的時間點時，發生事件對象的解釋變量的觀察值和其餘的潛在對象集合 (the risk set) 乘以他們各自的權重均值之差。(The residual compares the observed values of the explanatory variable for the case at a given event time with the weighted average of the explanatory variable in the risk set.) 重點是，這些個計算獲得的 Schoenfeld 殘差不應該和事件有任何的關係，如果繪製這些殘差和事件時間的散點圖，他們應該是呈現一種無序的狀態，也就說明了比例風險假設是沒有被違反的。(The residuals should not show any dependence on time – this would indicate that the proportional hazards assumptions is not met.)

實際操作中，更常用的是把這些 Schoenfeld 殘差調整之後的 “scaled Schoenfeld residuals”。調整後的 scaled Schoenfeld 殘差 的計算式是：

\[ r_{SS_{1j}} = d \times r_{S_{1j}} \text{var}(\hat\beta_1) \]

其中，

  • \(\text{var}(\hat\beta_1)\) 是該對數風險度比的方差。
  • \(d\) 是在該時間點時同時發生的事件計數

當比例風險前提得到滿足時，調整後的 scaled Schoenfeld residuals 的均值等於該變量的對數似然比。(The Scaled Schoenfeld residuals have a mean which is the true log hazard ratio under the proportional hazards assumption)。所以把調整後的 scaled Schoenfeld residuals 和時間做圖的話，繪製它隨着時間變化時的均值平滑曲線 (a smoothed average curve)，就能看出該變量的對數似然比，到底有沒有隨着時間的推進出現較大的波動。這樣的圖被叫做時間波動對數風險度比 (time-varying log-hazard ratio)。

Example 89.2 白血病患者數據，評估風險比例假設，當模型中增加了“治療組 \(\times\) 時間”的交互作用項之後，它的參數估計是 \(e^{\hat\gamma} = 1.008\)，它的信賴區間估計是 \((0.894, 1.137)\)，\(p = 0.894\)。似乎並沒有證據提示比例風險假設前提被違反。該數據的調整後 scaled Schoenfeld 殘差圖和時間之間關係的圖繪製在圖 89.1 中。

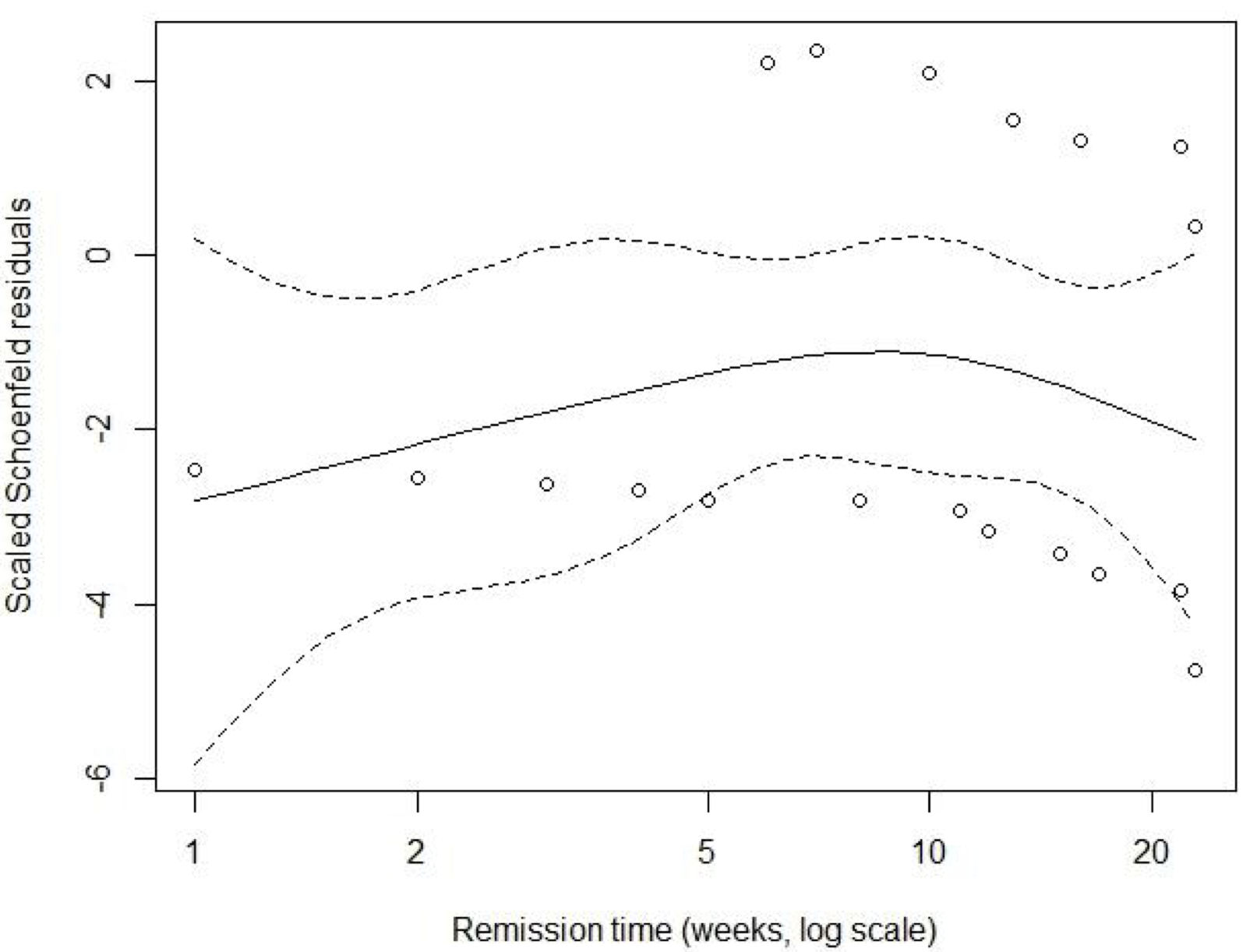
Plot of the scaled Schoenfeld residuals for the leukaemia patient data.

圖 89.1: Plot of the scaled Schoenfeld residuals for the leukaemia patient data.

Example 89.3 AGVHD數據，評估風險比例假設，在這個數據的例子中，我們給風險比例模型中加入了“治療組 \(\times\) 時間”的交互作用項之後，發現它的參數估計是 \(e^{\hat\gamma} = 0.854\)，它的信賴區間估計是 \((0.726, 1.003)\)，\(p = 0.055\)。似乎有跡象表明比例風險假設的前提沒有被滿足。這和我們繪製的生存曲線圖 89.2，還有調整後 scaled Schoenfeld 殘差圖 89.3 提示的一致。圖 89.3 中顯示的平滑曲線遠遠不能認爲是和橫軸近似平行的曲線。隨着時間的推移，該變量的對數風險度比很明顯是越來越小的。

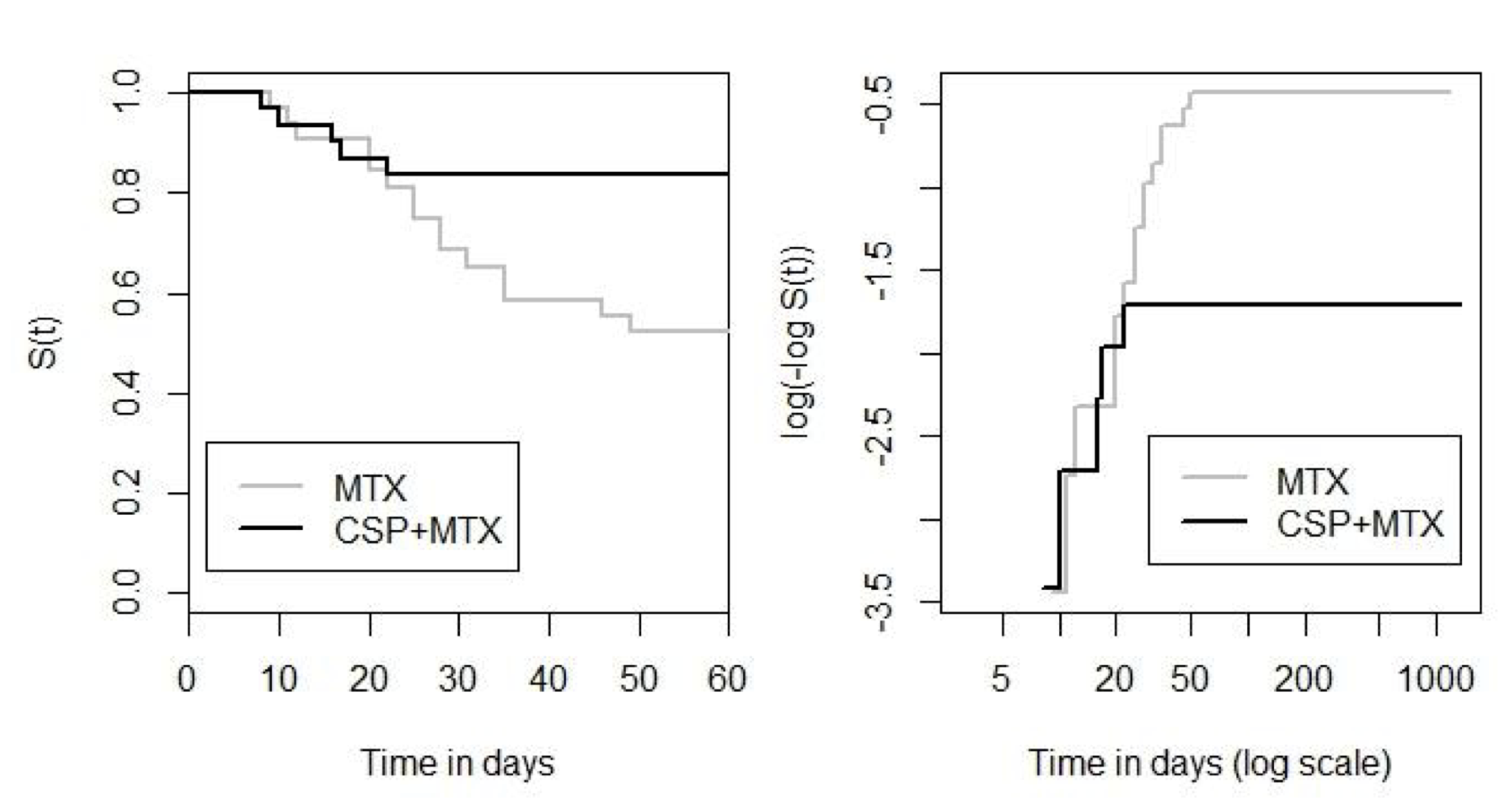
AGVHD data: plots of the estimated survivor curve in the two treatment groups.

圖 89.2: AGVHD data: plots of the estimated survivor curve in the two treatment groups.

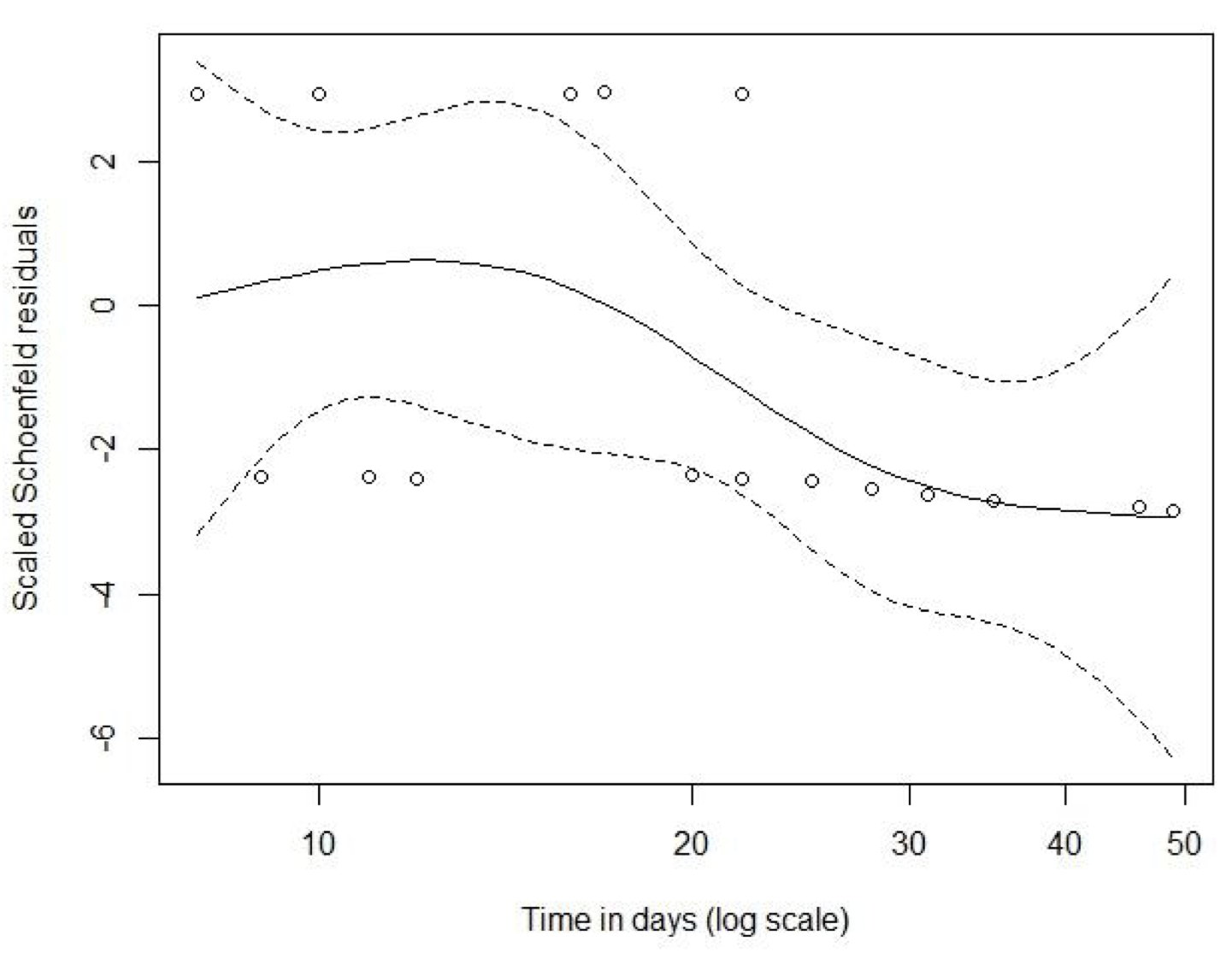
AGVHD data: plots of the scaled Schoenfeld residuals.

圖 89.3: AGVHD data: plots of the scaled Schoenfeld residuals.

Example 89.4 EPIC-Norfolk 隊列研究數據，評估乳癌發生的風險比例假設，在這個例子中我們建立了有三個解釋變量的模型，其中吸菸習慣還是一個有三個類別的變量。我們進一步用下列模型來分析每一個解釋變量的風險度比是否會隨時間發生變化：

\[ h(t;X) = h_0(t) \exp\{ \beta_1 X_{\text{alc}} + \beta_2 X_{\text{FH}} + \beta_3 X_{\text{former-smoker}} + \beta_4 X_{\text{current-smoker}} + \gamma_1 X_{\text{alc}}t + \gamma_2 X_{\text{FH}}t + \gamma_3 X_{\text{former-smoker}}t + \gamma_4 X_{\text{current-smoker}}t \} \]

上述模型估計的 \(\gamma\) 總結在下列表格中：

Parameter Estimate 95% CI p-value
Alcohol (\(\exp \gamma_1\)) 0.995 (0.995, 1.005) 0.306
Family history (\(\exp \gamma_2\)) 1.007 (0.978, 1.036) 0.656
Former smoker (\(\exp \gamma_3\)) 1.029 (1.008, 1.051) 0.008
Current smoker (\(\exp \gamma_4\)) 1.038 (1.005, 1.071) 0.022

對該模型的每一個解釋變量，都可以繪製相應的 scaled Schoenfeld 殘差圖。

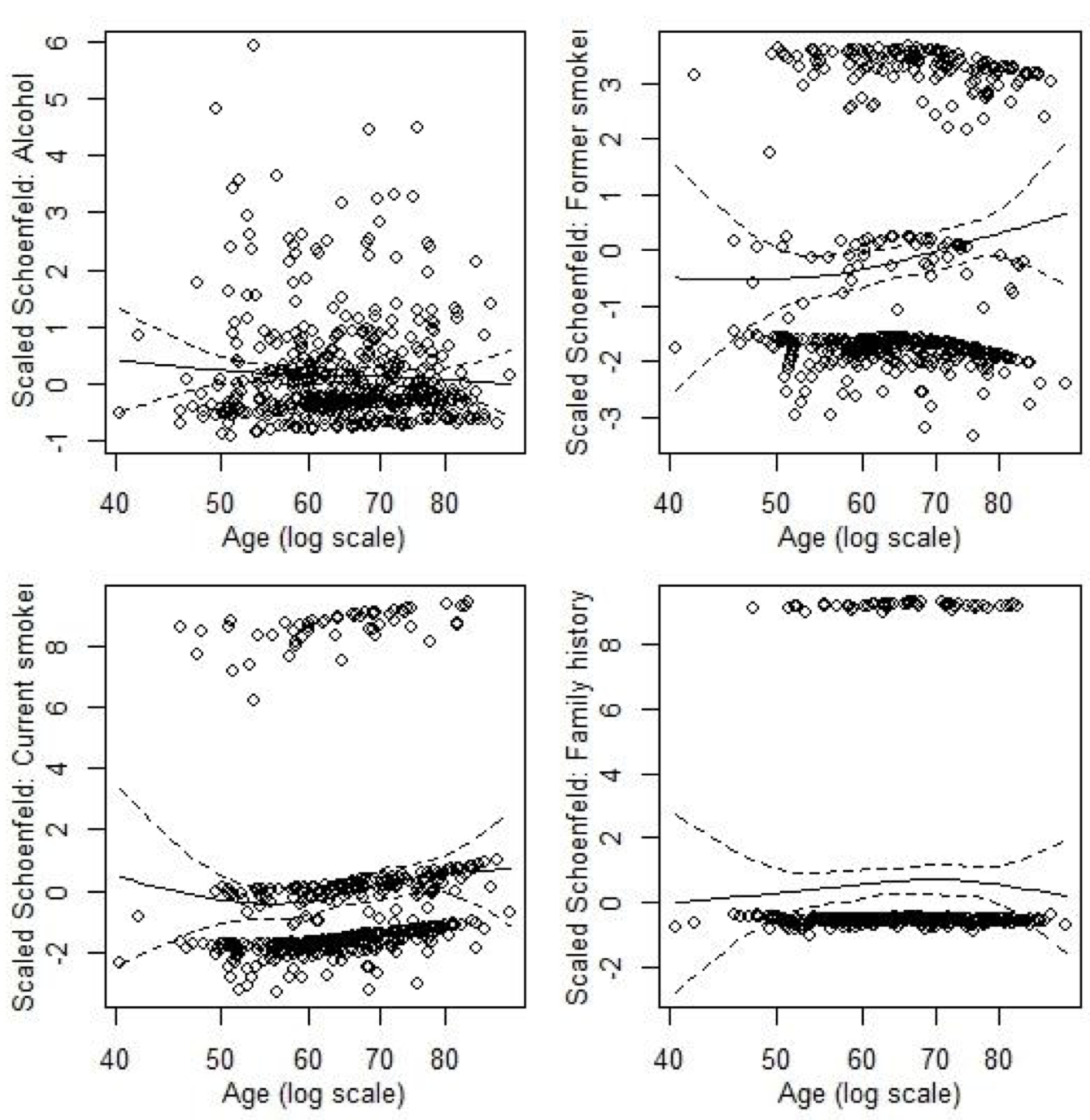
Plots of the scaled Schoenfeld residuals for the breast cancer data.

圖 89.4: Plots of the scaled Schoenfeld residuals for the breast cancer data.

89.6 評價模型擬合的其他有趣方法

89.6.1 Martingale 殘差-assessing the functional form of continuous variables

Matingale (馬丁哥?) 殘差圖可以用來輔助分析判斷生存回歸模型中連續型變量是否使用了合適的數學函數形式 (appropriate functional form)，因為有時候連續型變量需要增加該連續型變量的二次項或者多次項，也可能要用對數項之類的變形之後，才能完全把其與生存數據之間的關係完全解釋清楚。例如我們分析一個連續型變量 \(X\)，有許多時候可能需要把它進行數學轉換，那麼我們需要比較進行了數學轉換之前的模型和轉換之後的模型哪個更加合適：

\[ h(t; x) = h_0(t) \exp(\beta_1 \color{red}{x}) \text{ or } h(t; x) = h_0(t) \exp(\beta_1 \color{red}{\log x}) \]

一個 “Martingale” 殘差，其實是在描述實驗對象在所建立好的比例風險回歸模型估計的事件發生與否的殘差。它比較的是，該實驗對象在隨訪中是否真是觀察到事件發生，以及和模型中預測到該對象的最終事件發生與否之間的差值。A Martingale is a residual for an event process – it is the difference between what happened to a person (whether they had the event or not) and what is predicted to happen to a person under the model that has been fitted. The Martingale residual for individual i is:

\[ r_{M_i} = \delta_i - \hat H_0(t_i)\exp(\hat\beta x_i) \]

其中，

  • \(\delta_i\) 是該實驗對象 \(i\) 實際是 (=1) 否 (=0) 發生事件的指示變量
  • \(t_i\) 是生存時間，或者刪失時間
  • \(x_i\) 是解釋變量的向量
  • \(\hat H_0(t_i)\) 則是在時間點 \(t_i\) 時，該模型估計的累積基線風險 (estimated baseline cumulative hazard)
  • 如果模型正確，它就能接近100%準確地估計每一個實驗對象是否在對應的時間發生事件，且這個殘差之和應該等於零

這樣一個有趣的殘差，它之所以能幫助我們判斷連續型變量應有的數學函數形式，其實是要通過我們計算零模型 (沒有解釋變量的模型) 的 Martingale 殘差之後，繪製該殘差和你將要加入的連續變量（或轉換之後的形式）之間的散點圖。如果說模型中已有其他的非連續型變量，那麼上述的零模型可以指代沒有該連續變量的模型。

Example 89.5 白血病患者的觀察數據，分析患者的白細胞計數 (WBC)，白細胞的某種特性 AG (+/-)，以及死亡時間之間可能存在的關係：我們該如何處理 WBC 這個連續型變量？

首先，我們建立一個只有 AG 變量的 Cox 模型。此時獲得的 Martingale 殘差我們把它和連續型變量 WBC 做散點圖 89.5

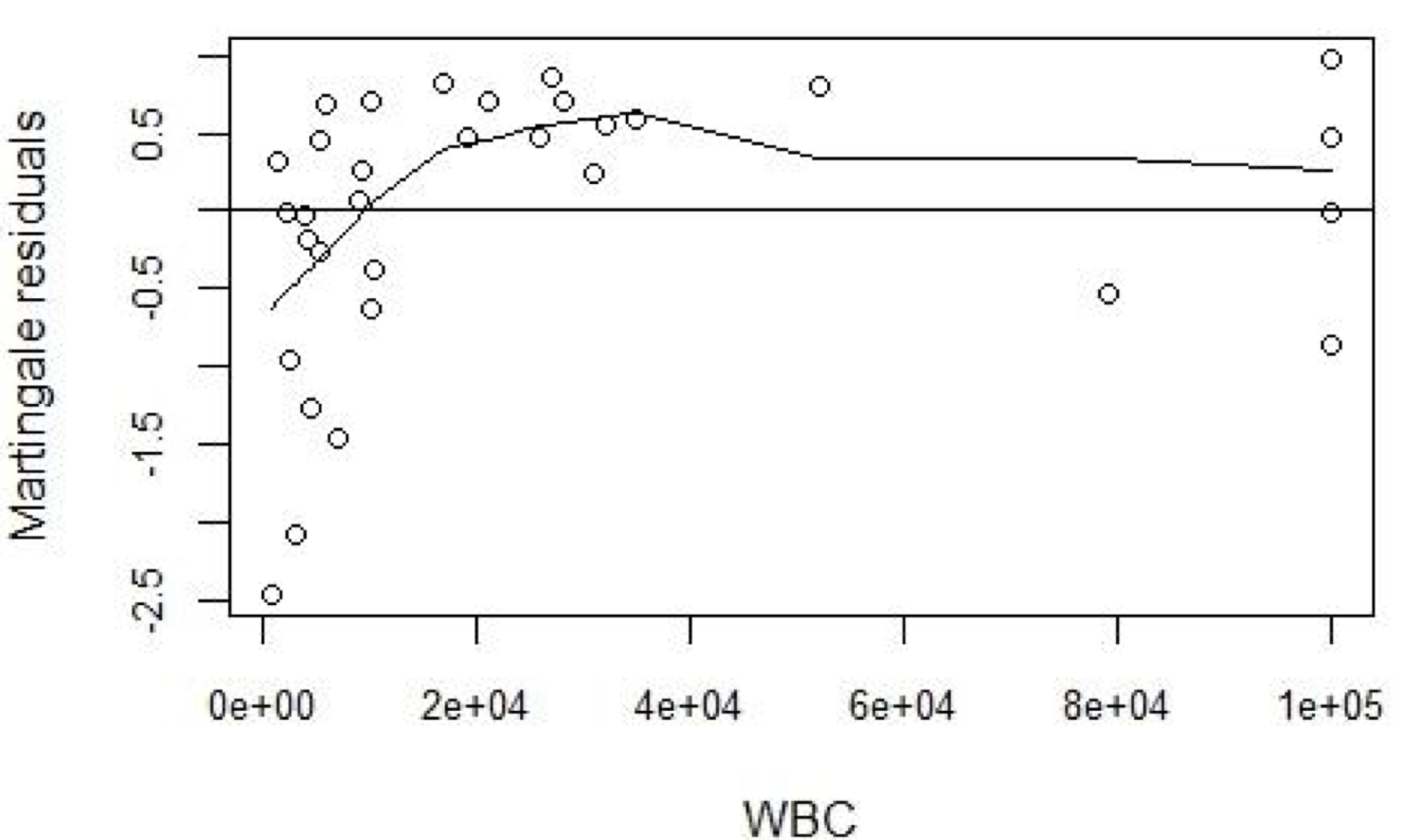
Plot of Martingale residuals (from a model with AG only) against WBC.

圖 89.5: Plot of Martingale residuals (from a model with AG only) against WBC.

假如該散點圖中的平滑曲線 (smoothed curve) 顯示爲接近一條直線，那麼我們可以認爲把 WBC 原封不動，連續型的單一變量放入模型中就可以，但是顯然圖中所示並非如此。那麼接下來該做的是，就是對 WBC 進行數學函數轉換 (transformation)。下圖 89.6 展示的是相同模型獲得的 Martingale 殘差和對數轉換之後的 WBC 繪製的散點圖，看起來似乎比之前原始數據的形式給出的散點圖更接近直線：

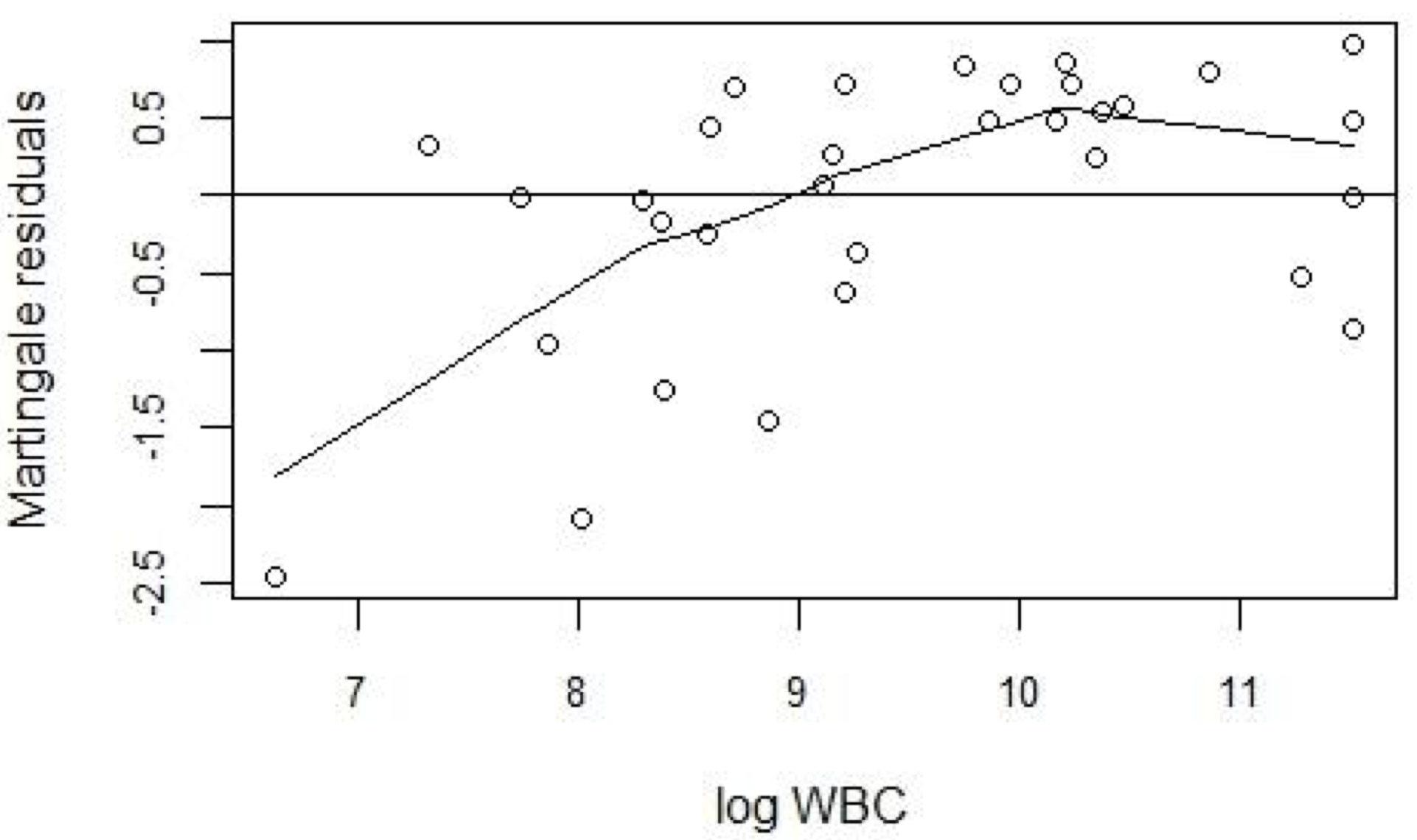
Plot of Martingale residuals (from a model with AG only) against log WBC.

圖 89.6: Plot of Martingale residuals (from a model with AG only) against log WBC.

那麼我們重新建立一個增加了 log WBC 而不是 WBC 本身的風險比例模型。

\[ h(t|AG,WBC) = h_0(t)e^(\beta_1 AG + \beta_2 \log(WBC)) \]

再計算獲取該模型的 Martingale 殘差，將之和 log WBC 繪製散點圖 89.7。如果這個變量的形式選對了，那麼此時的平滑曲線應該是接近橫軸的平線 (flat line)，顯然，這條平滑曲線接近平線的程度並不十分令人滿意。

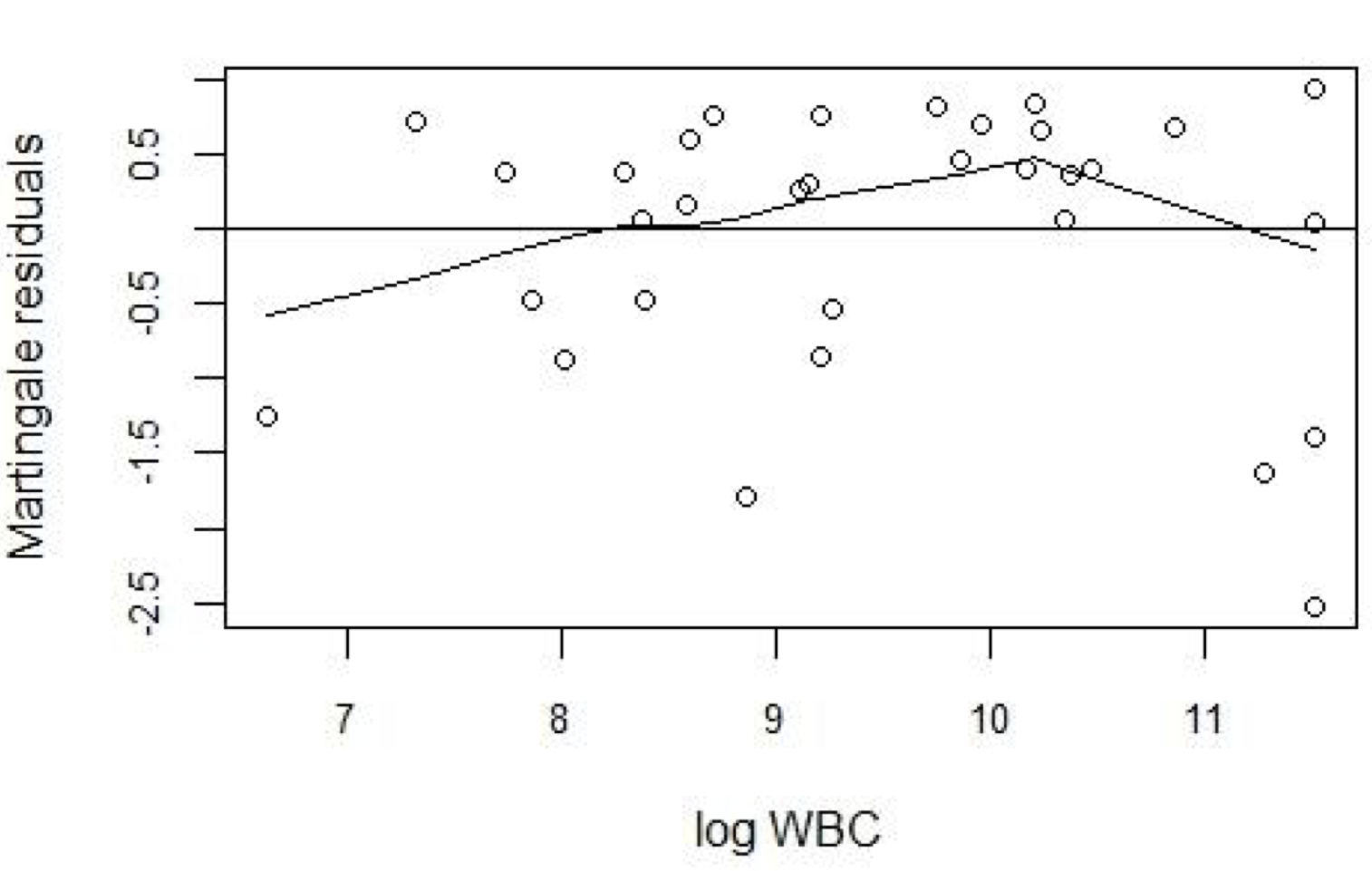
Plot of Martingale residuals (from a model with AG and log(WBC)) against log WBC.

圖 89.7: Plot of Martingale residuals (from a model with AG and log(WBC)) against log WBC.

當然，有人此時可能開始考慮把 WBC 白細胞計數這個變量本身給轉換成分類型變量（例如分成五個等分）。

\[ h(t|AG,WBC) = h_0(t)e^(\beta_1 AG + \beta_2 WBC_2 + \beta_3 WBC_3 + \beta_4 WBC_4 + \beta_5 WBC_5) \]

圖 89.8 顯示的是上述模型獲得的 Martingale 殘差和WBC之間的散點圖，及其獲得的平滑曲線；

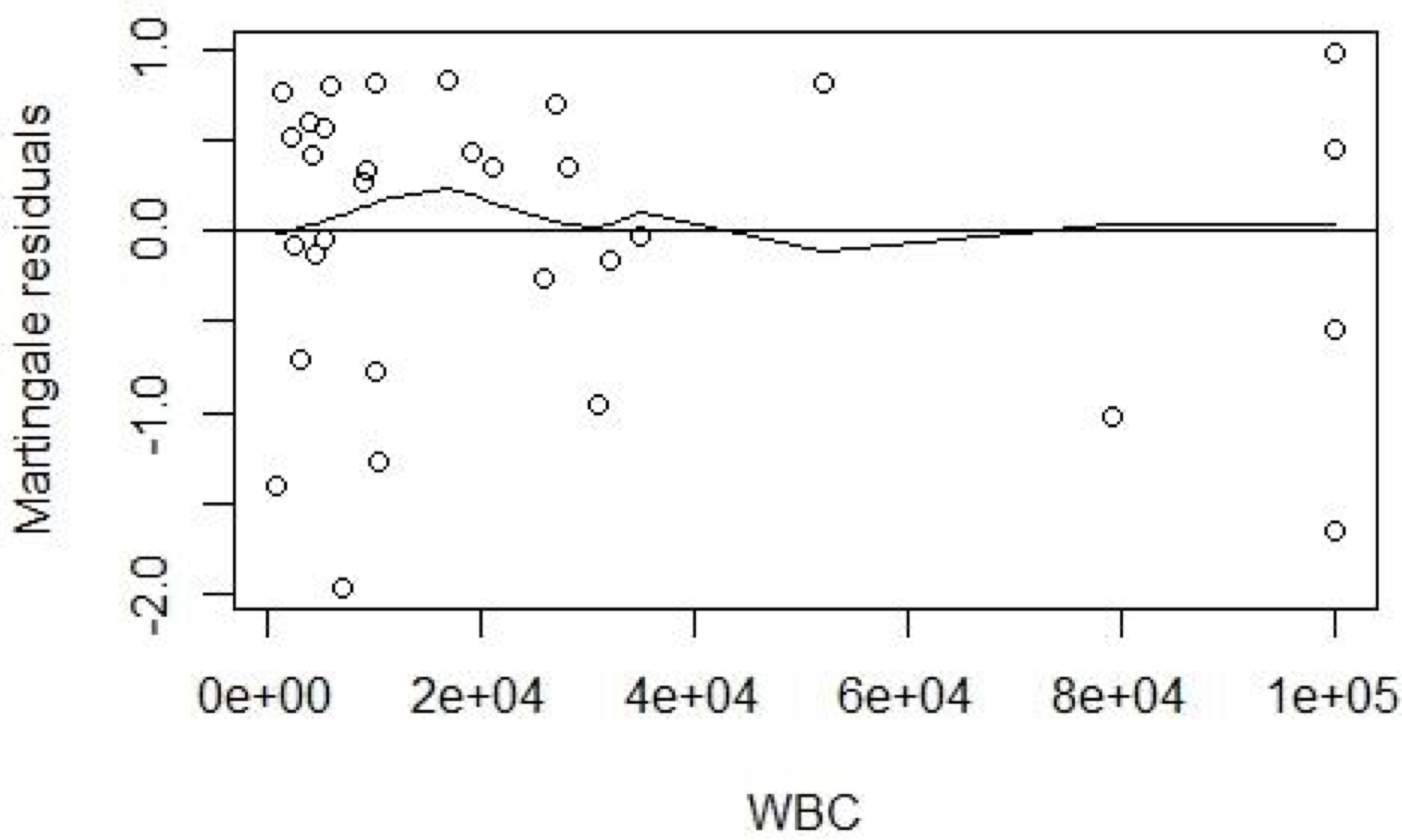
Plot of Martingale residuals (from a model with AG and categorized WBC) against WBC.

圖 89.8: Plot of Martingale residuals (from a model with AG and categorized WBC) against WBC.

似乎此時我們看見了最接近平線 (flat line) 的平滑曲線。但是通常情況下，其實我們並不期望把連續型變量人爲地分割成多類別變量。

89.6.2 Deviance 偏差殘差 – identifying individuals for whom the model does not provide a good fit

偏差殘差是馬丁哥殘差的轉換值，它的定義是:

\[ r_{D_i} = \text{sign}(r_{M_i})[-2\{r_{M_i} + \delta_i\log(\delta_i - r_{M_i})\}]^{\frac{1}{2}} \]

偏差殘差通過上面的公式，把模型給出的馬丁哥殘差轉換成為一組理論上應該是平均分佈在零兩側的數據。如果某個個體的偏差殘差過大，偏離0太遠的話，提示該模型對該個體數據擬合不佳。具體來說，如果偏差殘差遠大於零，提示的是該個體遠在模型預測他/她/它會發生事件的時間之前就已經發生了事件；相反如果偏差殘差遠小於零，則提示該個體在模型預測發生事件的時間點之後很晚才真的發生事件。

把偏差殘差作 Y 軸，危險度評分 (risk score \(=\beta^Tx\))，作 x 軸繪圖可以用於分析模型是否針對某些危險度高的人給出較高的偏差殘差，從而可以判斷模型是否合理。當判斷某些人可能偏差殘差過大，或者過小，之後要做的決定才是殘忍的，你要從數據中刪除這些個體？還是分析這些個體到底有哪些與眾不同的特質？或者是要重新對模型的各項解釋變量的形式進行修正？

在進行生存分析的時候，請一定要一邊構建模型，一邊用這些殘差來綜合分析模型的合理性。

89.7 Practical Survival 05

在本次練習中，繼續使用 PBC 數據。

89.7.1 把數據讀入你最喜歡的 R 的環境中，先考慮一個二進制變量 cir0 對生存的影響。在建立的模型中加入該 cir0 變量和時間的交互作用項。在 R 裏需要用到 tt() 命令。

pbcbase <- read.table("../backupfiles/pbcbase.csv", 
                      sep=",", header=T)
head(pbcbase)
##   id    datein   dateout     time d treat age     logb0c     alb0c  logigm0c cenc0 cir0 gh0 asc0
## 1  5 19feb1980 19sep1981 1.582478 1     1  46  1.0400000 -2.520001 -8.80e-01     1    0   0    0
## 2 22 22aug1980 22aug1980 0.000000 0     2  68  0.3999999  6.680000  7.90e-01     0    1   0    0
## 3 23 22jul1980 02aug1989 9.032169 0     2  65  0.0800000  7.680000  1.60e-01     0    0   0    0
## 4 40 08aug1980 21nov1982 2.286105 1     1  36  0.3999999  4.680000  7.00e-02     0    1   0    0
## 5 42 06sep1980 05oct1982 2.078029 1     1  38  0.8299999  4.680000 -1.19e-09     0    0   0    1
## 6 45 09feb1980 02jun1985 5.311430 1     1  48 -0.2600000  5.680000 -8.40e-01     1    0   0    0
##        bil0  alb0       igm0 bilcat
## 1 371.53520 31.78  0.3890451      3
## 2  85.11379 40.98 18.1970100      3
## 3  40.73803 41.98  4.2657950      2
## 4  85.11379 38.98  3.4673690      3
## 5 229.08670 38.98  2.9512090      3
## 6  18.62087 39.98  0.4265795      1
with(pbcbase, tabpct(treat, d, graph = FALSE))
## 
## Original table 
##        d
## treat      0    1  Total
##   1       45   49     94
##   2       50   47     97
##   Total   95   96    191
## 
## Row percent 
##      d
## treat       0       1  Total
##     1      45      49     94
##        (47.9)  (52.1)  (100)
##     2      50      47     97
##        (51.5)  (48.5)  (100)
## 
## Column percent 
##        d
## treat     0       %   1      %
##   1      45  (47.4)  49   (51)
##   2      50  (52.6)  47   (49)
##   Total  95   (100)  96  (100)
##question 1##

cir0.model<- coxph(Surv(time,d)~cir0+tt(cir0), data=pbcbase, tt=function(x,t,...) {x*t})
summary(cir0.model)
## Call:
## coxph(formula = Surv(time, d) ~ cir0 + tt(cir0), data = pbcbase, 
##     tt = function(x, t, ...) {
##         x * t
##     })
## 
##   n= 191, number of events= 96 
## 
##              coef exp(coef) se(coef)       z   Pr(>|z|)    
## cir0      1.52149   4.57902  0.36632  4.1534 0.00003276 ***
## tt(cir0) -0.16368   0.84901  0.10278 -1.5926     0.1113    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##          exp(coef) exp(-coef) lower .95 upper .95
## cir0       4.57902    0.21839   2.23336    9.3883
## tt(cir0)   0.84901    1.17784   0.69411    1.0385
## 
## Concordance= 0.628  (se = 0.028 )
## Likelihood ratio test= 24.38  on 2 df,   p=5e-06
## Wald test            = 25.28  on 2 df,   p=3e-06
## Score (logrank) test = 28.81  on 2 df,   p=6e-07

可以看到，cir0 和時間交互作用項的風險度比估計值是 0.849， 意思其實是，log(0.849) = -0.164 是該變量每增加一年的隨訪時間對死亡風險度的額外影響 (is the additional effect on the hazard for cirrhosis for each additional year of follow-up time)。對該交互作用項的回歸係數是否等於零的 Wald 檢驗提示並沒有有意義的交互作用。也就是該變量對發生死亡風險度的影響並不會隨時間改變。所以，無證據提示比例風險假設被違背。該模型的數學表達式可以寫作：

\[ h(t;x) = h_0(t)\exp(\beta x + \gamma xt) \]

89.7.2 繪製模型中只有 cir0 一個變量的情況下，調整後的 scaled Schoenfeld 殘差圖。

##question 2##

cir0.cox<-coxph(Surv(time,d)~cir0,data=pbcbase)
time.dep.zph <- cox.zph(cir0.cox, transform = 'identity')
time.dep.zph
##        chisq df     p
## cir0   2.602  1 0.107
## GLOBAL 2.602  1 0.107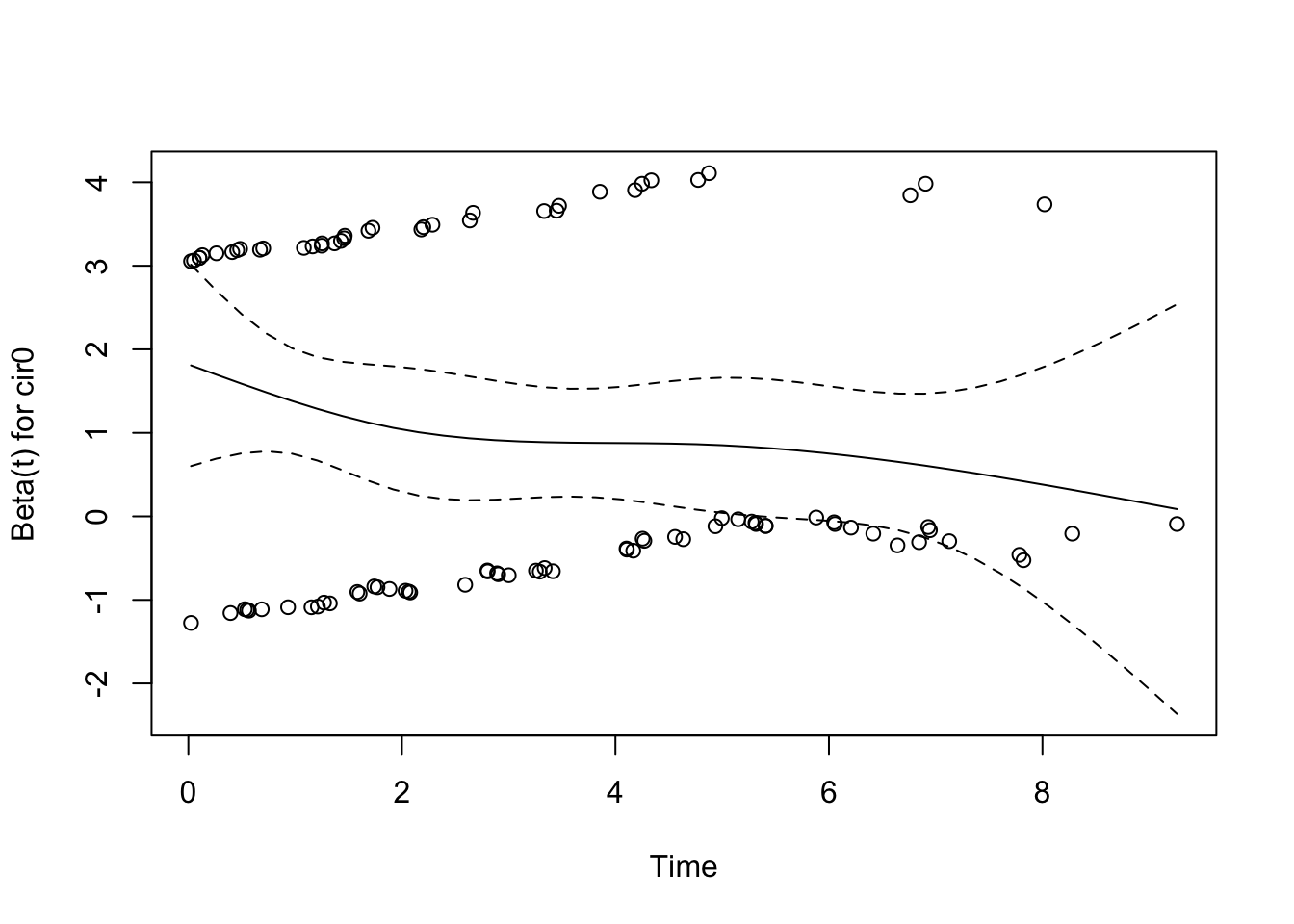
plot(time.dep.zph)
Test of PH assumption.

圖 89.9: Test of PH assumption.

儘管途中顯示似乎殘差和時間有那麼一點點關係，但是平滑曲線好像又有點接近平線 (flat line)。該卡方檢驗其實檢驗的是該圖中繪製的平滑曲線是否和平線相同。p = 0.11說明沒有證據提示該變量有違反風險比例假設。

89.7.3 另外一種探索變量 cir0 的風險度比是否隨時間保持不變的方法是可以把生存數據分割成幾個時間段，分別估計每個時間段內該暴露變量的風險度比。

  1. 在隨訪時間的中位數 2.85 年時把數據分割成兩部分，使用 survSplit 命令
  2. 使用 cir0 和分割好的時間段之間的交互作用項建立模型，看該交互作用項的風險度比是否有意義。
# Remove zero survival times
pbc1<-pbcbase[!(pbcbase$time==0),]

pbc.split<- survSplit(Surv(time,d)~., pbc1, cut=c(2.85,12), end="time", event="d", start="time0", episode="tiband")

cir0.model.tiband1<- coxph(Surv(time,d)~cir0,data=pbc.split[pbc.split$tiband==1,])
cir0.model.tiband2<- coxph(Surv(time,d)~cir0,data=pbc.split[pbc.split$tiband==2,])

summary(cir0.model.tiband1)
## Call:
## coxph(formula = Surv(time, d) ~ cir0, data = pbc.split[pbc.split$tiband == 
##     1, ])
## 
##   n= 184, number of events= 48 
## 
##         coef exp(coef) se(coef)      z  Pr(>|z|)    
## cir0 1.30766   3.69751  0.29049 4.5016 6.745e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##      exp(coef) exp(-coef) lower .95 upper .95
## cir0    3.6975    0.27045    2.0924    6.5339
## 
## Concordance= 0.655  (se = 0.035 )
## Likelihood ratio test= 19.63  on 1 df,   p=9e-06
## Wald test            = 20.26  on 1 df,   p=7e-06
## Score (logrank) test = 23.28  on 1 df,   p=1e-06
summary(cir0.model.tiband2)
## Call:
## coxph(formula = Surv(time, d) ~ cir0, data = pbc.split[pbc.split$tiband == 
##     2, ])
## 
##   n= 111, number of events= 48 
## 
##         coef exp(coef) se(coef)   z Pr(>|z|)  
## cir0 0.70356   2.02093  0.33503 2.1  0.03573 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##      exp(coef) exp(-coef) lower .95 upper .95
## cir0    2.0209    0.49482     1.048     3.897
## 
## Concordance= 0.564  (se = 0.034 )
## Likelihood ratio test= 3.89  on 1 df,   p=0.05
## Wald test            = 4.41  on 1 df,   p=0.04
## Score (logrank) test = 4.59  on 1 df,   p=0.03
cir0.model.tiband<- coxph(Surv(time,d)~cir0*as.factor(tiband),data=pbc.split)
## Warning in coxph.fit(X, Y, istrat, offset, init, control, weights = weights, : Loglik converged
## before variable 2 ; coefficient may be infinite.
summary(cir0.model.tiband)
## Call:
## coxph(formula = Surv(time, d) ~ cir0 * as.factor(tiband), data = pbc.split)
## 
##   n= 295, number of events= 96 
## 
##                                coef   exp(coef)    se(coef)       z  Pr(>|z|)    
## cir0                     1.3077e+00  3.6975e+00  2.9049e-01  4.5016 6.745e-06 ***
## as.factor(tiband)2      -1.9011e+01  5.5393e-09  2.6264e+03 -0.0072    0.9942    
## cir0:as.factor(tiband)2 -6.0410e-01  5.4657e-01  4.4343e-01 -1.3623    0.1731    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##                          exp(coef) exp(-coef) lower .95 upper .95
## cir0                    3.6975e+00 2.7045e-01   2.09240    6.5339
## as.factor(tiband)2      5.5393e-09 1.8053e+08   0.00000       Inf
## cir0:as.factor(tiband)2 5.4657e-01 1.8296e+00   0.22919    1.3034
## 
## Concordance= 0.755  (se = 0.018 )
## Likelihood ratio test= 77.11  on 3 df,   p=<2e-16
## Wald test            = 24.67  on 3 df,   p=2e-05
## Score (logrank) test = 79.03  on 3 df,   p=<2e-16
cir0.model.tt<- coxph(Surv(time,d)~cir0+tt(cir0),data=pbc, tt=function(x,t,...) {x*(t<2.85)})
summary(cir0.model.tt)
## Call:
## coxph(formula = Surv(time, d) ~ cir0 + tt(cir0), data = pbc, 
##     tt = function(x, t, ...) {
##         x * (t < 2.85)
##     })
## 
##   n= 191, number of events= 96 
## 
##             coef exp(coef) se(coef)      z Pr(>|z|)  
## cir0     0.70356   2.02093  0.33503 2.1000  0.03573 *
## tt(cir0) 0.60410   1.82960  0.44343 1.3623  0.17309  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##          exp(coef) exp(-coef) lower .95 upper .95
## cir0        2.0209    0.49482    1.0480    3.8970
## tt(cir0)    1.8296    0.54657    0.7672    4.3632
## 
## Concordance= 0.628  (se = 0.028 )
## Likelihood ratio test= 23.53  on 2 df,   p=8e-06
## Wald test            = 24.67  on 2 df,   p=4e-06
## Score (logrank) test = 27.87  on 2 df,   p=9e-07

我們發現在第一個時間段內， cir0 的風險度比是 3.70，第二個時間段內，相同的參數估計是 2.02。但是你看他們二者的信賴區間有相當的重疊部分，所以事實上還是沒有證據證明風險比例假設有被違反的痕跡。

89.7.4 接下來我們來看該數據集中的一個連續型變量， bil0 。我們練習使用 Martingale 殘差輔助我們判斷該連續型變量應該放入模型中的數學函數形式。

##question 4##

empty.cox<-coxph(Surv(time,d)~1,data=pbcbase)
mgale_res<-resid(empty.cox,type="martingale")
plot(pbc$bil0,mgale_res)
lines(lowess(pbc$bil0,mgale_res))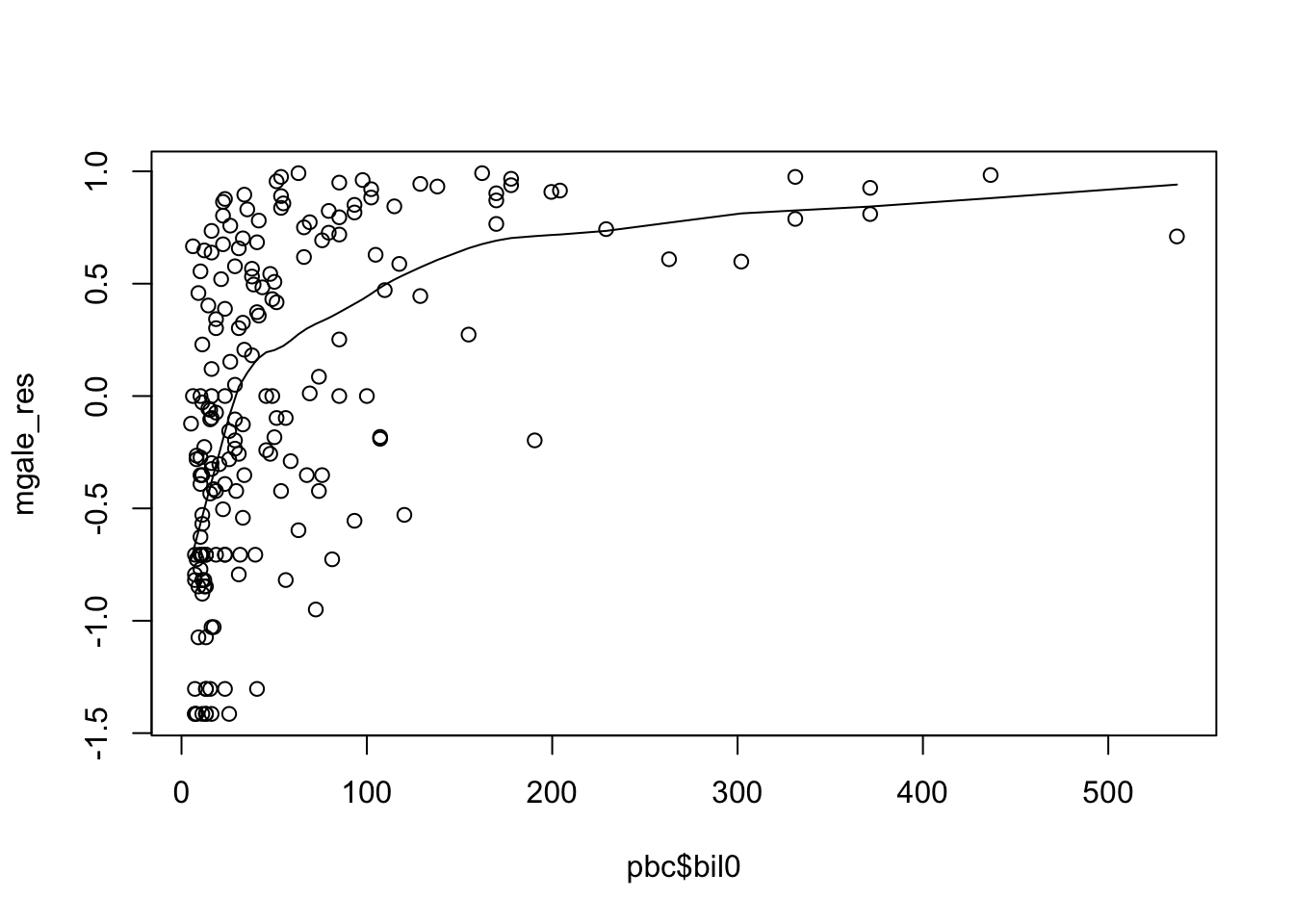
Martingale residuals from empty model and bi10 variable.

圖 89.10: Martingale residuals from empty model and bi10 variable. 

pbcbase$log_bil0<-log(pbcbase$bil0)
plot(pbcbase$log_bil0,mgale_res)
lines(lowess(pbcbase$log_bil0,mgale_res))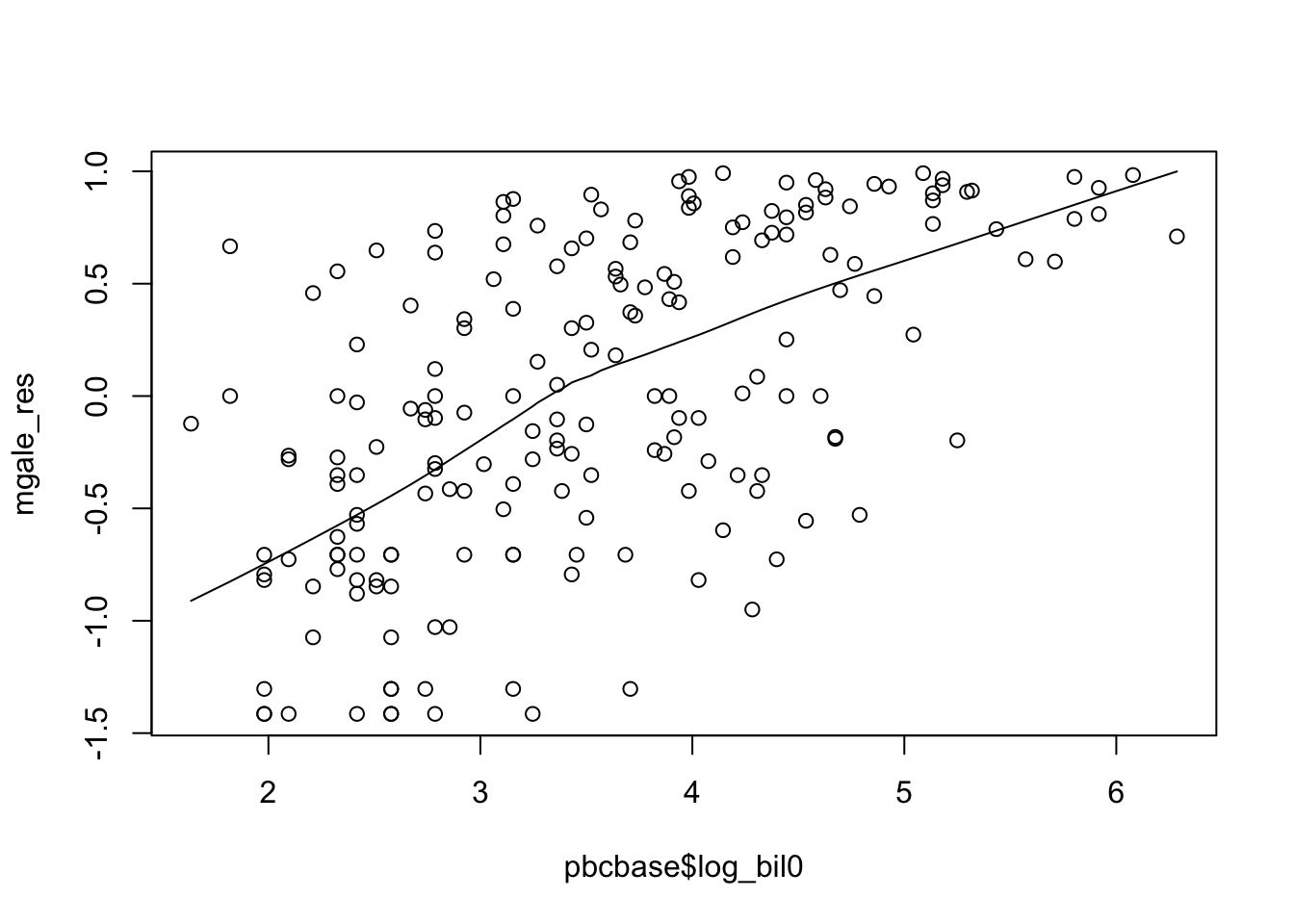
Martingale residuals from empty model and log bil0 variable.

圖 89.11: Martingale residuals from empty model and log bil0 variable.

圖 89.10 給出的平滑曲線顯然不能認爲是直線 (linear)。似乎提示應該把連續型變量做自然對數的轉換 (log transformation)。而進行了對數轉換之後的 Martingale 殘差和對數 bil0 之間呈現了較爲接近直線的關係。

89.7.5 選擇你認爲應該對 bil0 進行的數學函數形式，使用 Scaled Schoenfeld 殘差檢查它是否違反比例風險假設。

##question 5##

log_bil0.cox<-coxph(Surv(time,d)~log_bil0,data=pbcbase)
time.dep.zph <- cox.zph(log_bil0.cox, transform = 'identity')
time.dep.zph
##            chisq df    p
## log_bil0 0.04634  1 0.83
## GLOBAL   0.04634  1 0.83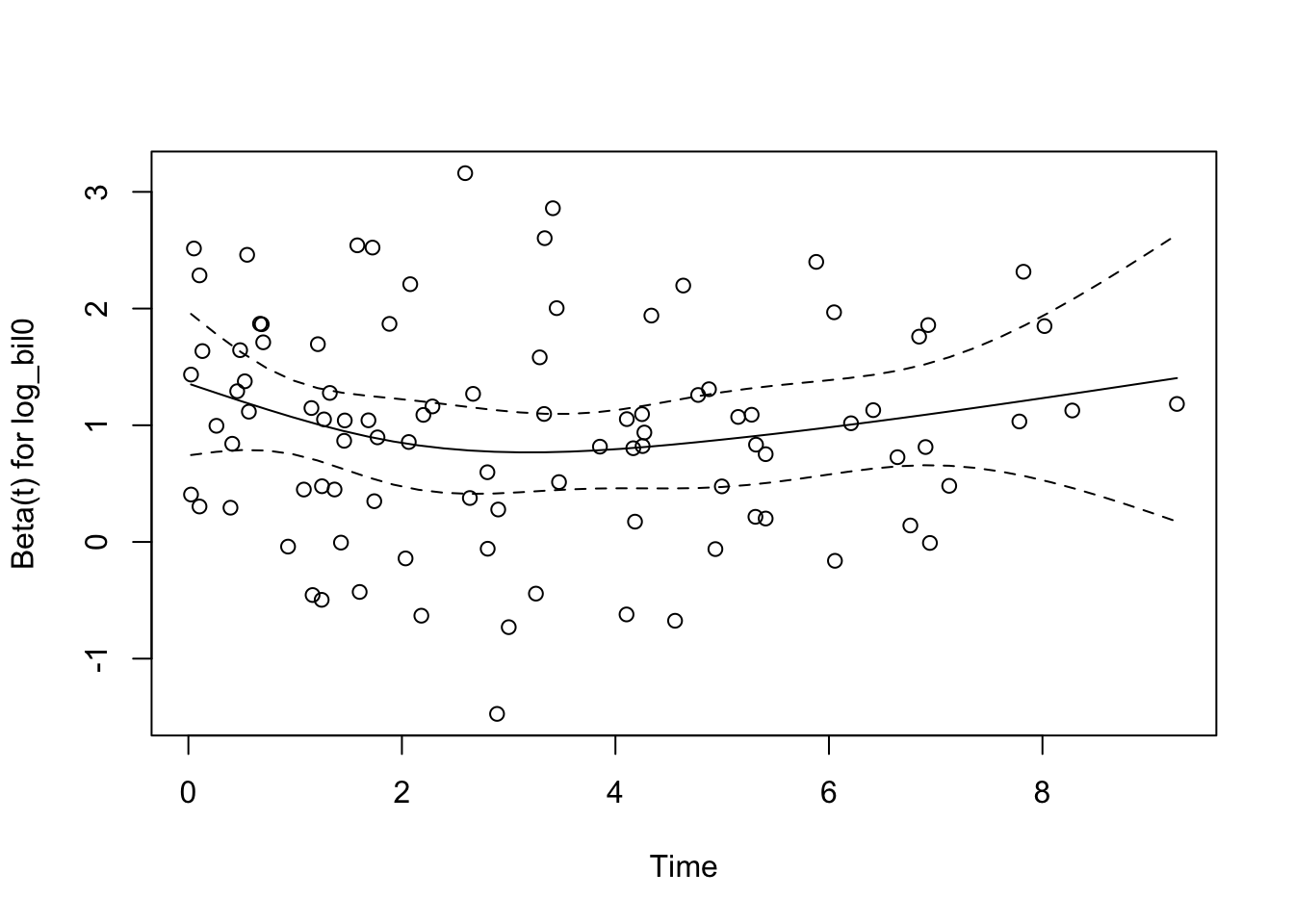
plot(time.dep.zph)
Scaled Schoenfeld residuals from Cox model with log bil0.

圖 89.12: Scaled Schoenfeld residuals from Cox model with log bil0. 

log_bil0.cox.tt<-coxph(Surv(time,d)~log_bil0+tt(log_bil0),data=pbcbase, tt=function(x,t,...) {x*t})
summary(log_bil0.cox.tt)
## Call:
## coxph(formula = Surv(time, d) ~ log_bil0 + tt(log_bil0), data = pbcbase, 
##     tt = function(x, t, ...) {
##         x * t
##     })
## 
##   n= 191, number of events= 96 
## 
##                   coef exp(coef)  se(coef)       z  Pr(>|z|)    
## log_bil0      1.006343  2.735578  0.173300  5.8070 6.362e-09 ***
## tt(log_bil0) -0.010890  0.989169  0.050591 -0.2153    0.8296    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##              exp(coef) exp(-coef) lower .95 upper .95
## log_bil0       2.73558    0.36555   1.94776    3.8420
## tt(log_bil0)   0.98917    1.01095   0.89579    1.0923
## 
## Concordance= 0.777  (se = 0.023 )
## Likelihood ratio test= 82.89  on 2 df,   p=<2e-16
## Wald test            = 84.05  on 2 df,   p=<2e-16
## Score (logrank) test = 94.31  on 2 df,   p=<2e-16

89.7.6 建立一個含有如下解釋變量的 Cox 比例風險回歸模型：轉換過後的bil0, cir0，cenc0, Age

  1. 寫下該模型的數學表達式

\[ h(t; x) = h_0(t)\exp (\beta_1 \text{treat} + \beta_2 \text{log_bil10} + \beta_3 \text{cir0} + \beta_4 \text{cenc0} + \beta_5 \text{age}) \]

  1. 使用 R 建立該模型並作出估計。
##question 6##

big.model<-coxph(Surv(time,d)~as.factor(treat)+cir0+log_bil0+cenc0+age,data=pbcbase)
summary(big.model)
## Call:
## coxph(formula = Surv(time, d) ~ as.factor(treat) + cir0 + log_bil0 + 
##     cenc0 + age, data = pbcbase)
## 
##   n= 191, number of events= 96 
## 
##                        coef exp(coef)  se(coef)       z  Pr(>|z|)    
## as.factor(treat)2 -0.403828  0.667759  0.210281 -1.9204  0.054805 .  
## cir0               1.011903  2.750830  0.227946  4.4392 9.029e-06 ***
## log_bil0           1.070331  2.916344  0.131845  8.1181 4.735e-16 ***
## cenc0              0.896650  2.451377  0.273444  3.2791  0.001041 ** 
## age                0.049802  1.051063  0.011305  4.4053 1.056e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##                   exp(coef) exp(-coef) lower .95 upper .95
## as.factor(treat)2   0.66776    1.49755   0.44221    1.0083
## cir0                2.75083    0.36353   1.75969    4.3002
## log_bil0            2.91634    0.34290   2.25223    3.7763
## cenc0               2.45138    0.40793   1.43435    4.1895
## age                 1.05106    0.95142   1.02803    1.0746
## 
## Concordance= 0.819  (se = 0.021 )
## Likelihood ratio test= 132.22  on 5 df,   p=<2e-16
## Wald test            = 108.28  on 5 df,   p=<2e-16
## Score (logrank) test = 135.55  on 5 df,   p=<2e-16

在其他模型解釋變量保持不變的條件下，治療組相比對照組死亡的風險度下降了近 44%。如果在基線時患者本身已經有肝硬化 cir0 = 1，是沒有肝硬化的患者的死亡風險度的 2.75 倍。年齡每增加 1 歲，死亡風險增加 5% 左右。患者如果在基線時已經有膽汁淤滯 (cenc0 = 1)，該患者的死亡風險度是沒有膽汁淤滯患者的死亡風險度的2.45 倍。在對數尺度上，每增加一個單位的 bil0，死亡風險度增加接近3倍。

我們可以使用下面的代碼和圖形來診斷年齡應該有的數學函數形式：

big.model.notage<-coxph(Surv(time,d)~as.factor(treat)+cir0+log_bil0+cenc0,data=pbcbase)
mgale_res<-resid(big.model.notage,type="martingale")
plot(pbcbase$age,mgale_res)
lines(lowess(pbcbase$age,mgale_res))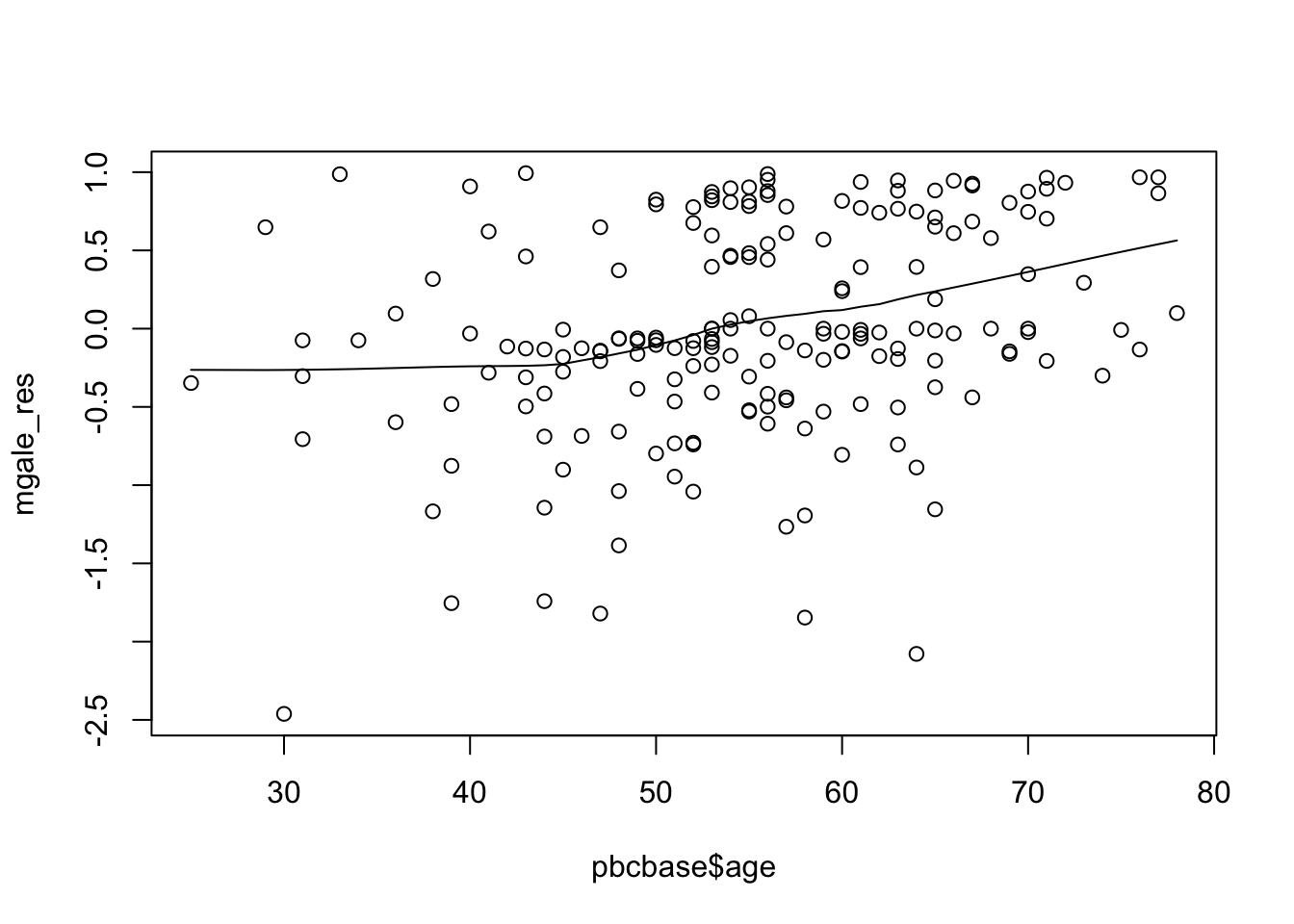
Martingale residuals suggest that there may be a non-linear effect of age.

圖 89.13: Martingale residuals suggest that there may be a non-linear effect of age. 

#adding in age^2

big.model.agesq<-coxph(Surv(time,d)~as.factor(treat)+cir0+log_bil0+cenc0+age+I(age^2),data=pbcbase)
summary(big.model.agesq)
## Call:
## coxph(formula = Surv(time, d) ~ as.factor(treat) + cir0 + log_bil0 + 
##     cenc0 + age + I(age^2), data = pbcbase)
## 
##   n= 191, number of events= 96 
## 
##                          coef   exp(coef)    se(coef)       z  Pr(>|z|)    
## as.factor(treat)2 -0.44766397  0.63911941  0.21761762 -2.0571  0.039675 *  
## cir0               1.00260646  2.72537617  0.22669204  4.4228 9.744e-06 ***
## log_bil0           1.09029781  2.97515998  0.13485536  8.0849 6.219e-16 ***
## cenc0              0.82992173  2.29313924  0.28452399  2.9169  0.003536 ** 
## age               -0.02251409  0.97773747  0.08410094 -0.2677  0.788928    
## I(age^2)           0.00065222  1.00065243  0.00075564  0.8631  0.388067    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##                   exp(coef) exp(-coef) lower .95 upper .95
## as.factor(treat)2   0.63912    1.56465   0.41720   0.97908
## cir0                2.72538    0.36692   1.74770   4.24998
## log_bil0            2.97516    0.33612   2.28413   3.87525
## cenc0               2.29314    0.43608   1.31293   4.00514
## age                 0.97774    1.02277   0.82915   1.15295
## I(age^2)            1.00065    0.99935   0.99917   1.00214
## 
## Concordance= 0.819  (se = 0.021 )
## Likelihood ratio test= 132.93  on 6 df,   p=<2e-16
## Wald test            = 109.72  on 6 df,   p=<2e-16
## Score (logrank) test = 137.67  on 6 df,   p=<2e-16
mgale_res<-resid(big.model.agesq,type="martingale")
plot(pbcbase$age,mgale_res)
lines(lowess(pbcbase$age,mgale_res))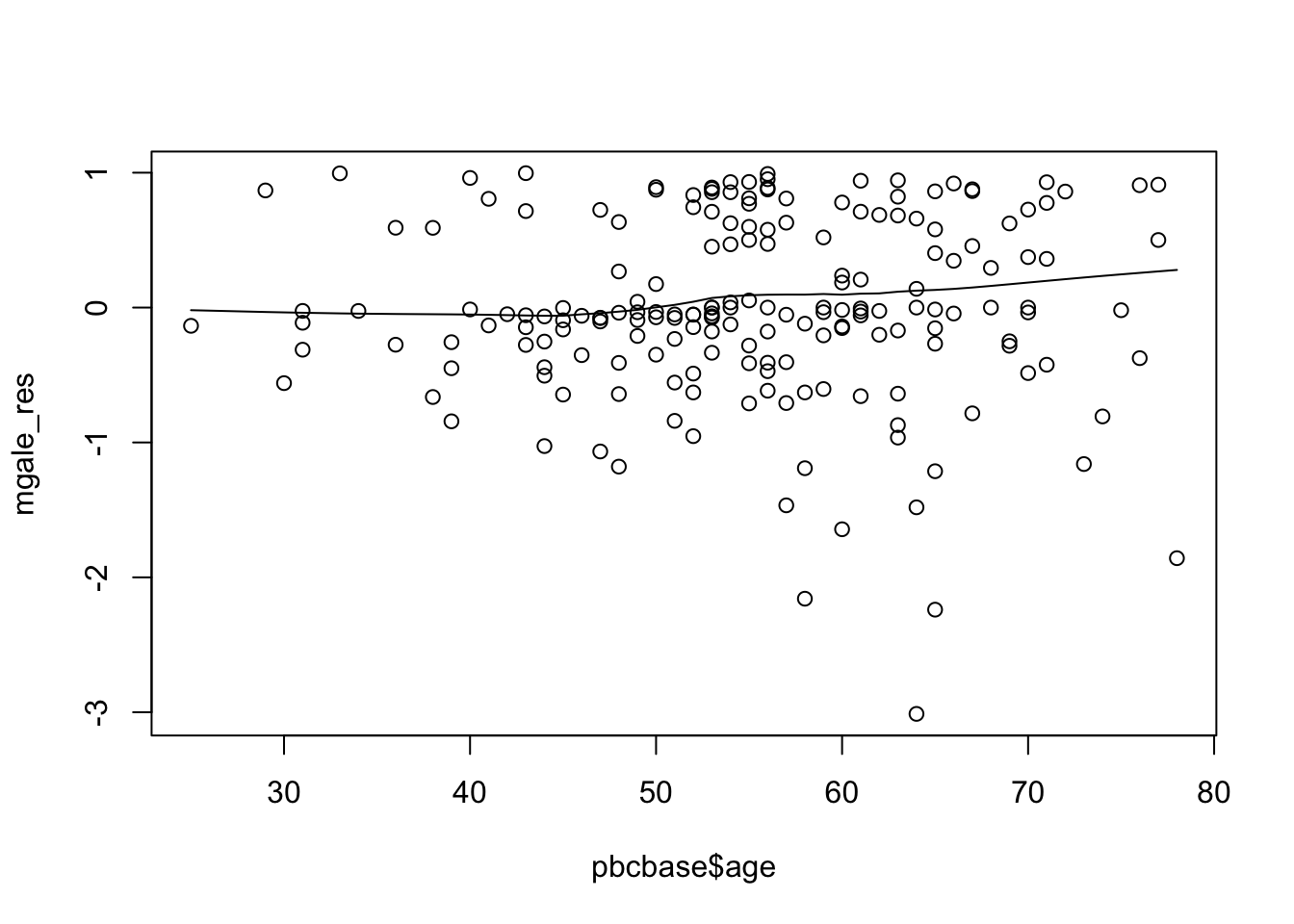
Martingale residuals adding a quadratic term of age.

圖 89.14: Martingale residuals adding a quadratic term of age.

重新評估對數轉換之後的 bil0 是否違反了比例風險假設

#re-assessing the form for log_bilirubin

big.model<-coxph(Surv(time,d)~as.factor(treat)+cir0+log_bil0+cenc0+age,data=pbcbase)
mgale_res<-resid(big.model,type="martingale")
plot(pbcbase$log_bil0,mgale_res)
lines(lowess(pbcbase$log_bil0,mgale_res))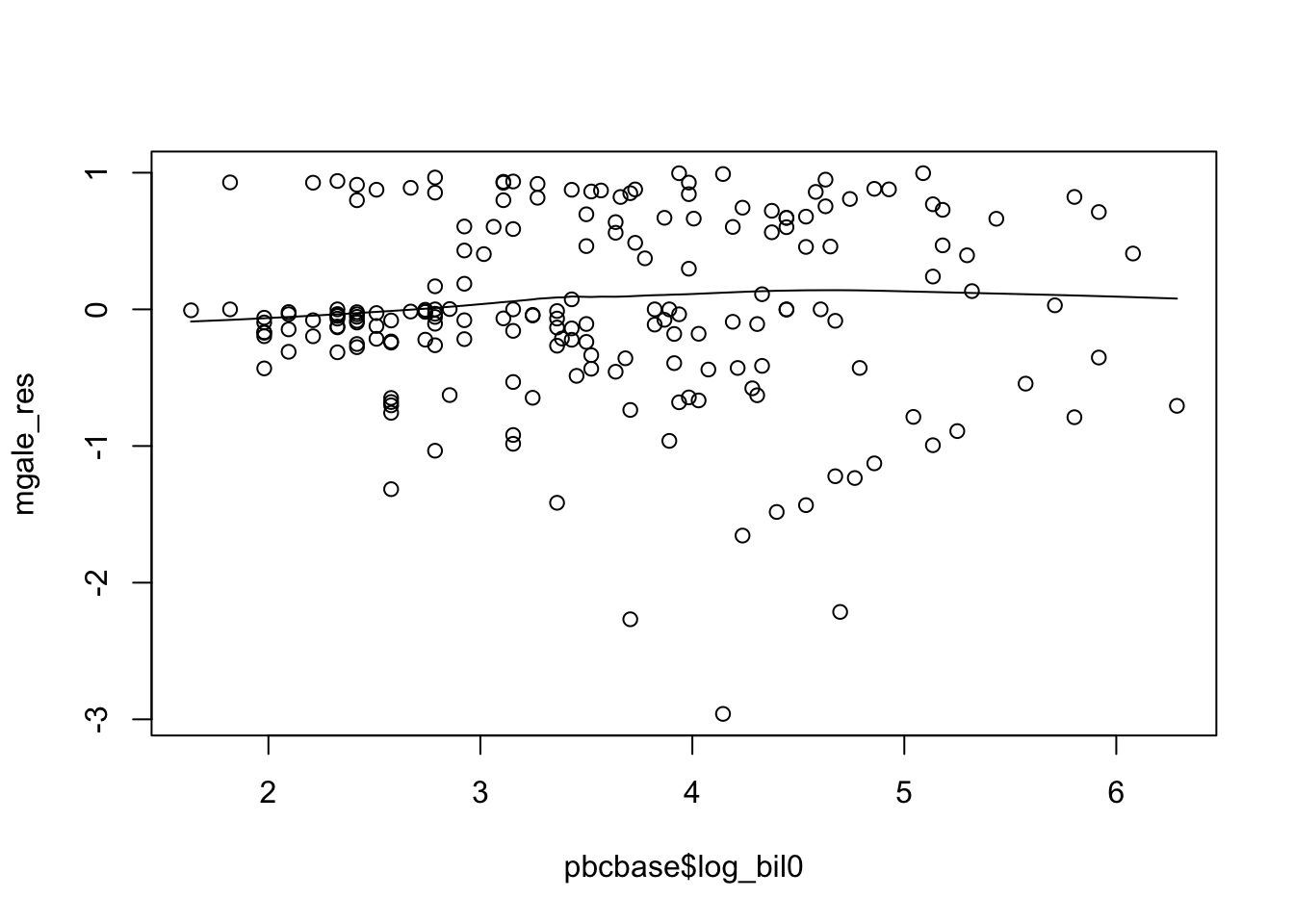
Martingale residuals with log bil0.

圖 89.15: Martingale residuals with log bil0.

令人滿意的圖。

#Schoenfeld test

big.model.zph <- cox.zph(big.model, transform = 'identity')
big.model.zph
##                    chisq df     p
## as.factor(treat) 1.50021  1 0.221
## cir0             0.57141  1 0.450
## log_bil0         0.02714  1 0.869
## cenc0            0.90385  1 0.342
## age              0.07815  1 0.780
## GLOBAL           2.53437  5 0.771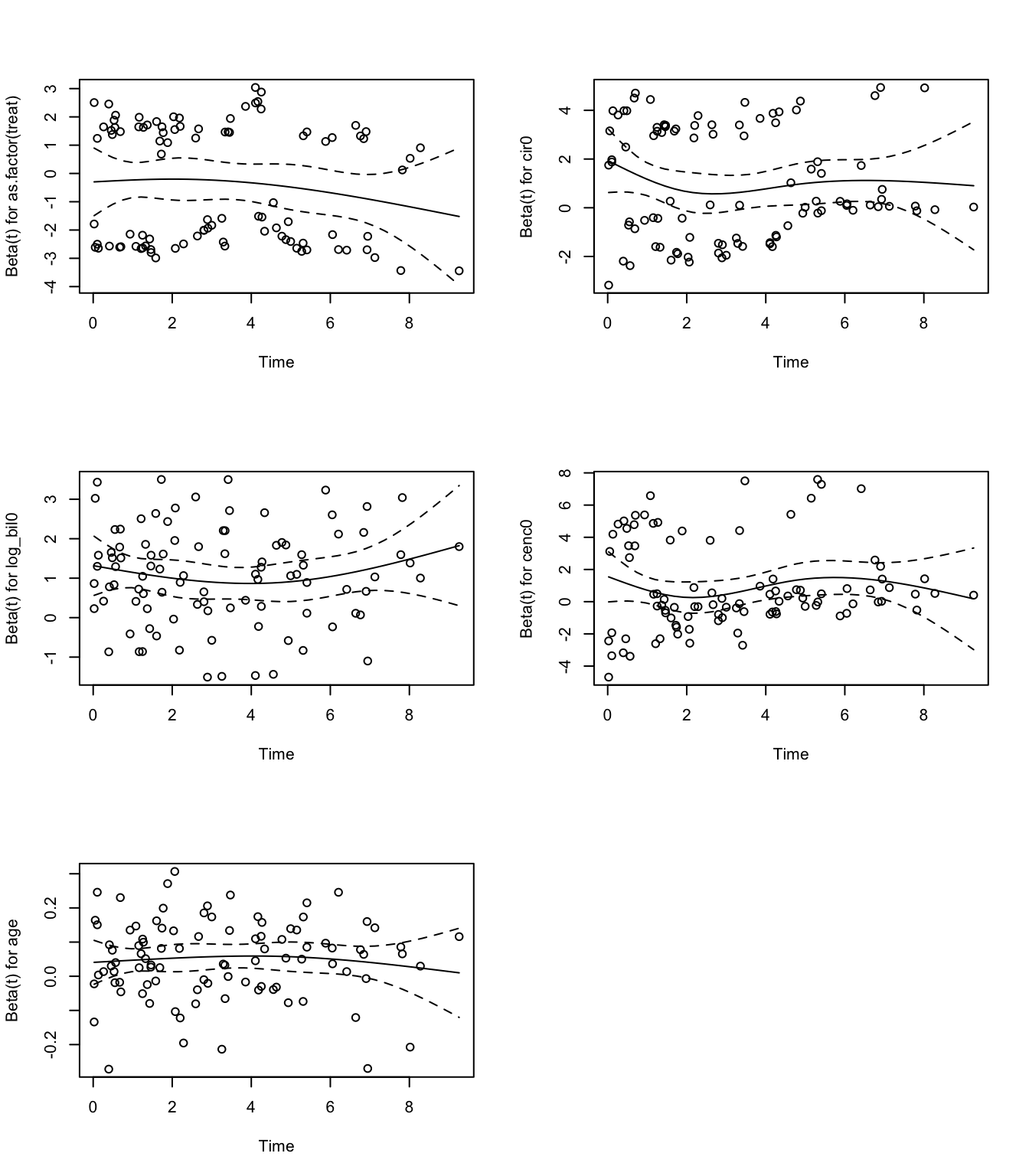
par(mfrow=c(3,2))
plot(big.model.zph)
Scaled Schoenfeld residuals plot from Cox model for each covariate.

圖 89.16: Scaled Schoenfeld residuals plot from Cox model for each covariate.

Schoenfeld 殘差圖及其檢驗結果也提示無違反風險比例的跡象。

89.7.6.1 觀察該模型的偏差殘差圖

##question 7##

#deviance residuals##
  
devres<-resid(big.model,type="deviance")
plot(devres,xlab="index", ylab="Deviance residuals",cex.lab=1.3)
abline(h=0)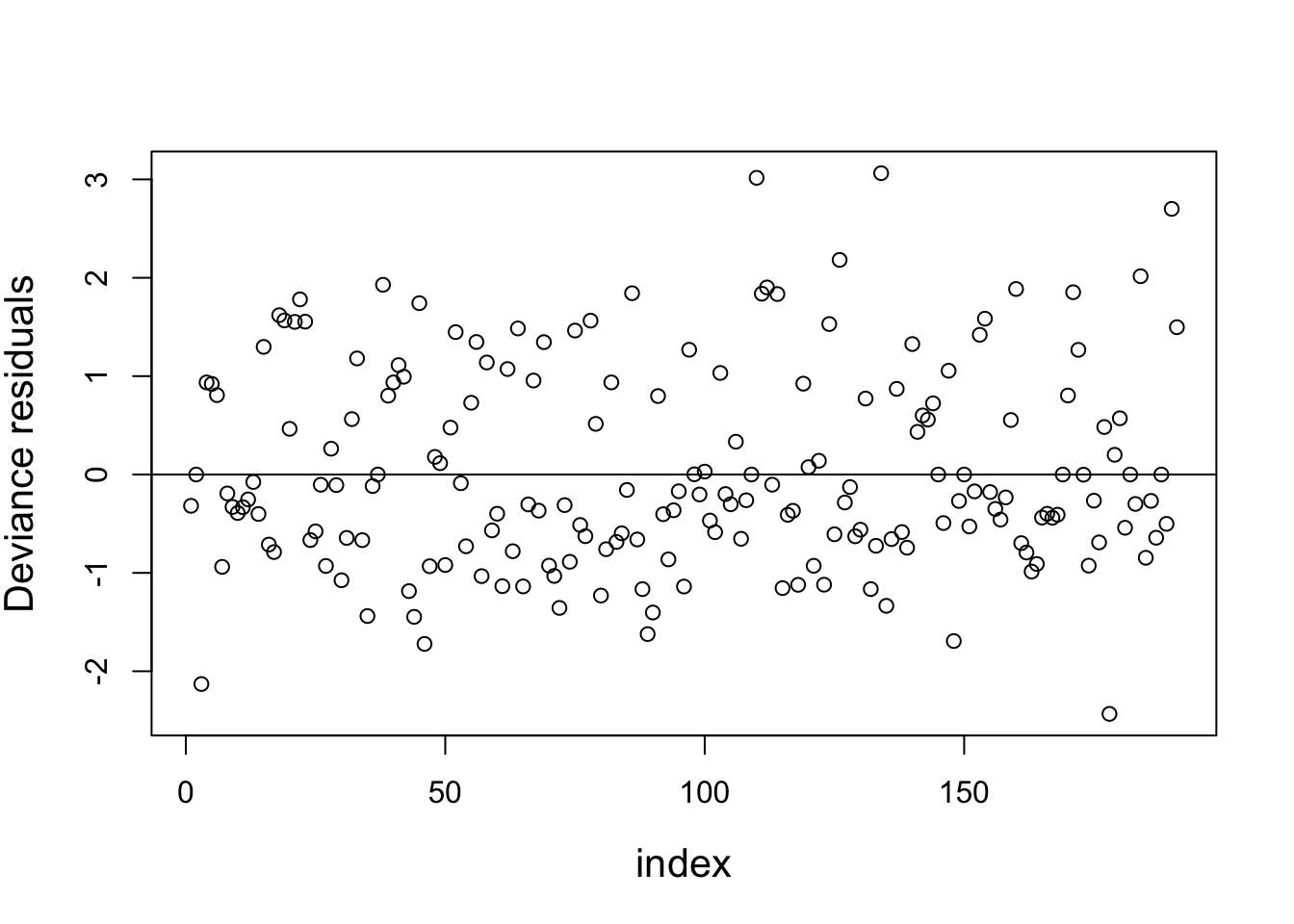

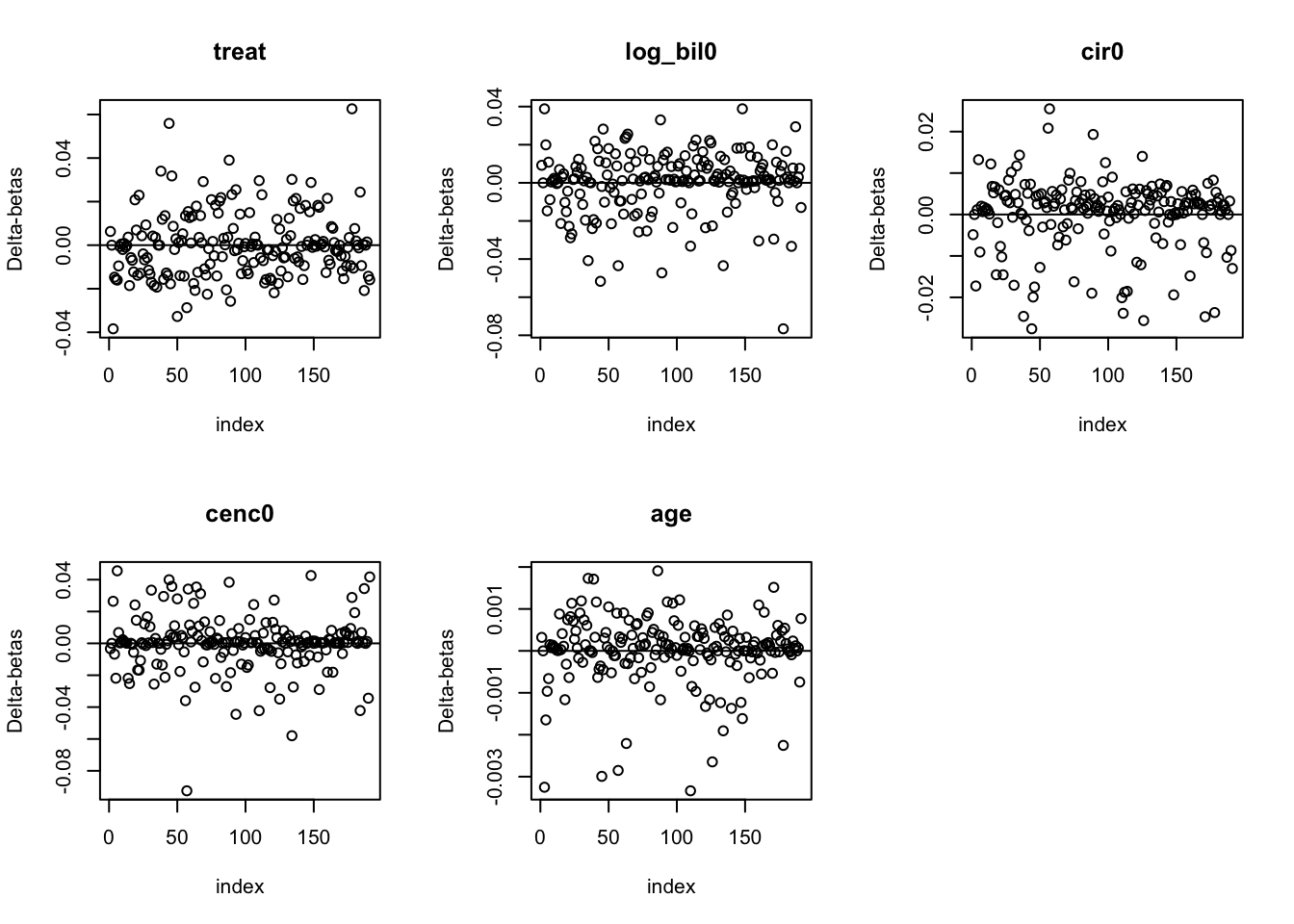
#delta betas
  
delta.betas<-resid(big.model,type="dfbeta")
par(mfrow=c(2,3))

plot(delta.betas[,1],xlab="index",ylab="Delta-betas",main="treat")
abline(h=0)
plot(delta.betas[,2],xlab="index",ylab="Delta-betas",main="log_bil0")
abline(h=0)
plot(delta.betas[,3],xlab="index",ylab="Delta-betas",main="cir0")
abline(h=0)
plot(delta.betas[,4],xlab="index",ylab="Delta-betas",main="cenc0")
abline(h=0)
plot(delta.betas[,5],xlab="index",ylab="Delta-betas",main="age")
abline(h=0)