第 57 章 重要概念複習

There are no routine statistical questions, only questionable statistical routines.
Sir David Cox
The Generalised Linear Regression lectures were orgainised and taught by Professor Chris Frost.

57.1 概率論學派統計推斷要點複習

下面我們一起用二項分佈的概念 (\(n\) 個對象中 \(K\) 個“事件”)，來複習概率論學派的統計推斷要點。

  1. 模型，the Model。一個統計模型，描述的不僅僅是我們研究的人羣的一些特徵，而且通常一個模型還可提供如何從人羣中收集該樣本的信息。
    用二項分佈的概念來解釋，人羣是衆多個體的集合，他們中的一部分佔比 \(\pi\) 的人身上發生了某個事件。從這個人羣的集合中，我們隨機抽取 \(n\) 個對象作爲研究樣本，該樣本中有 \(K\) 個人身上發生了事件。此時，我們說 \(K\) 服從人羣比例爲 \(\pi\) 的二項分佈：\(K \sim \text{Bin}(n,\pi)\)。
  2. 參數，parameters。模型中的參數反映了人羣的某些特徵。在實際應用中，從來沒有“人類”能知道人羣參數的真實值，渺小的我們從人羣中抽取樣本，用於推斷 “上帝才知道的” 這些代表了人羣特徵的參數。
    在二項分佈的情境下，有且只有一個人羣參數，人羣中事件的比例 \(\pi\)。
  3. 參數估計量，parameter estimators。估計量是樣本的統計量，被用來估計未知的總體參數。估計量 estimator，是一個隨機變量，是我們計算估計值的一般形式。估計值 estimate，是每個樣本通過統計模型計算獲得的估計量的真實值，每採樣一次，計算獲得的估計值理論上會略有不同。
    二項分佈的上下文中，人羣事件比例 – 這一參數 \(\pi\) 的天然估計量是 \(\hat\pi = \frac{K}{n}\)，當一個樣本中發現 \(K = k\)，該樣本給出的估計值是 \(\frac{k}{n}\)。
  4. 研究假設，hypotheses。研究假設是實驗前我們提出的要被檢驗的一些關於人羣某些特徵參數的 “陳述 statement”。可以是猜想參數等於某個特定值，或者多個參數大小相同。
    二項分佈的數據裏，只有一個人羣參數，\(\pi\)。可能提出的零假設和替代假設有很多，\(\pi = 0.5 \text{ v.s. } \pi \neq 0.5\) 是其中之一的複合型假設。

57.2 似然

如果一個模型只有一個參數 \(\theta\)，樣本數據已知的話，該參數的似然爲：

\[\text{L}(\theta | \text{data}) = \text{Pr}(\text{data}|\theta)\]

其中，\(\text{Pr}(\text{data}|\theta)\) 對於離散型變量，是概率方程 probability function；對於連續型變量，則是概率密度方程 probability density function (PDF)。

對數似然，就是上面的似然方程取自然底數的對數方程：

\[\ell(\theta | \text{data}) = \text{ln}\{ \text{L}(\theta | \text{data}) \}\]

57.3 極大似然估計

當數據收集完畢，從獲得的數據中計算獲得的能夠使似然方程/或對數似然方程取得極大值的 \(\theta\) 的大小，被叫做極大似然估計 \(\text{(MLE)}\)，且通常數學標記會在參數上加一頂帽子： \(\hat\theta\)。收集不同的樣本，在相同的似然方程或對數似然方程下，極大似然估計不同。

  1. 許多問題，我們獲得極大似然估計的方法是先定義好模型的似然方程，然後求該方程的一階導數之後計算使之等於零的參數值大小就是 \(\text{MLE } \hat\theta\)。此時，你還要記得再求一次二階導數，看是否小於零，以確保前一步計算獲得的值給出的似然方程是極大值。
  2. 更多的時候我們用對數似然方程以簡化計算過程：

\[ \begin{aligned} \left.\frac{\text{d}}{\text{d } \theta}\ell (\theta | \text{data})\right\vert_{\theta=\hat{\theta}} &= \ell^\prime(\hat\theta) = 0 \\ \left.\frac{\text{d}^2}{\text{d } \theta^2}\ell (\theta | \text{data})\right\vert_{\theta=\hat{\theta}} &= \ell^{\prime\prime}(\hat\theta) < 0 \end{aligned} \]

  1. 我們只關心似然方程的形狀，所以方程中不包含參數的部分可全部忽略掉。
  2. \(\text{MLE}\) 的一些關鍵性質：
    1. 漸進無偏 asymptotically unbiased：當 \(n\rightarrow \infty\) 時，\(E(\hat\theta) \rightarrow \theta\)；
    2. 一致性 consistency：隨着樣本量的增加，\(\hat\theta\) 收斂於 (converges) 總體參數 \(\theta\)；
    3. 漸進正態分佈 asymptotically normality：隨着樣本量增加，\(\hat\theta\) 的樣本分佈收斂於 (converges) 正態分佈，方差爲 \[E[-\ell^{\prime\prime}(\theta)]^{-1}=[-\ell^{\prime\prime}(\hat\theta)]^{-1}\]
    4. 恆定性 invariance：如果 \(\hat\theta\) 是 \(\text{MLE}\)，那麼 \(\theta\) 被數學轉換以後 \(g(\theta)\) 的方程的 \(\text{MLE}\) 是 \(g(\hat\theta)\)
  3. 似然理論可以直接拓展到多個參數的情況。一般地，如果一個模型有 \(p\) 個參數 \(\mathbf{\theta} = (\theta_1, \theta_2, \cdots, \theta_p)^T\)，這些參數在給定數據的條件下的似然方程爲：\[\text{L}(\mathbf{\theta} | \text{data}) = \text{Pr}(\text{data} | \mathbf{\theta})\] 其中，概率 (密度) 方程在多個參數時變成聯合 (joint) 概率 (密度) 方程。似然，也是各個參數的聯合似然方程。此時，參數向量 \(\mathbf{\theta} = (\theta_1, \theta_2, \cdots, \theta_p)^T\) 的方差協方差矩陣的估計量爲：

\[ \hat{\text{Var}}(\mathbf{\hat\theta}) = - \left( \begin{array}{c} \frac{\partial^2\ell}{\partial\theta^2_1} & \frac{\partial^2\ell}{\partial\theta_2\partial\theta_1} & \cdots & \frac{\partial^2\ell}{\partial\theta_k\partial\theta_1} \\ \frac{\partial^2\ell}{\partial\theta_1\partial\theta_2} & \frac{\partial^2\ell}{\partial\theta^2_2} & \cdots & \frac{\partial^2\ell}{\partial\theta_k\partial\theta_2} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2\ell}{\partial\theta_1\partial\theta_k} & \frac{\partial^2\ell}{\partial\theta_2\partial\theta_k} & \cdots & \frac{\partial^2\ell}{\partial\theta^2_k} \\ \end{array} \right)^{-1}_{\theta=\hat\theta} \]

Tips: typing vcov(Modelname) command in R will display this estimated variance-covariance matrix for the parameter estimates.

回到二項分佈數據的例子：

\[ K \sim \text{Bin}(n, \pi) \]

如果我們樣本的觀測數據是 \(K=k\)，對數似然方程一次微分等於零以後求得的參數 \(\pi\) 的 \(\text{MLE}\) 是 \(\hat\pi = \frac{k}{n}\)。所以參數 \(\pi\) 的估計量是 \(\frac{K}{n}\)。\(\hat\pi\) 的方差估計量是：

\[ \hat{\text{Var}} (\hat\pi) = \frac{\hat\pi(1-\hat\pi)}{n} \text{ for } \hat\pi = \frac{k}{n} \]

57.4 關於假設檢驗的複習

極大似然估計可以有三大類檢驗方法：似然比檢驗法 likelihood ratio test；Wald 檢驗 Wald test；Score 檢驗 Score test。

  • 似然比檢驗法 likelihood ratio test (LRT) (Section 16.2)：

\[ -2llr(\theta_0) = -2\{ \ell(\theta_0) - \ell(\hat\theta) \} \]

零假設條件下 (Under \(\text{H}_0\):)

\[ -2llr(\theta_0) \sim \chi_1^2 \]

這個對數似然比的統計量可以和自由度爲 1 的卡方分佈作比較，計算反對零假設的證據的強度大小。如果顯著性水平是 \(\alpha\)，那麼下面條件成立時，可以認爲反對零假設的證據強度大到足以拒絕零假設。

\[ -2llr(\theta_0) > \chi^2_{1, 1-\alpha} \]

  • Wald 檢驗 (Section 16.4) 是一種利用二次方程近似法對似然比檢驗進行近似的手段。其檢驗統計量是

\[ \begin{aligned} (\frac{M-\theta_0}{S})^2 & \sim \chi^2_1 \\ \text{Where } M & = \hat\theta \\ S^2 & = \frac{1}{-\ell^{\prime\prime}(\hat\theta)} \end{aligned} \]

  • Score 檢驗 (Section 16.5) 是另一種利用二次方程近似法對似然比檢驗進行近似的手段。其檢驗統計量是

\[ \begin{aligned} \frac{U^2}{V} & \sim \chi^2_1 \\ \text{Where } U & = \ell^\prime(\theta_0) \\ V & = -\ell^{\prime\prime}(\theta_0) \end{aligned} \]

如果對數似然方程本身就是一個二次方程 (數據服從完美正態分佈狀態，且總體方差已知時)，這三大類的檢驗法其實計算獲得完全一樣的 \(p\) 值，提供完全一致的證據。多數情況下，三大類檢驗法的結果是近似的。關於三種檢驗法的比較可以參考過去總結的章節 (Section 16.6)

57.4.1 子集似然函數

當統計模型中的部分參數是噪音參數 (nuisance parameters) 時，我們需要用到子集似然函數法 (Section 19) 來去除噪音參數的影響,，只檢驗我們感興趣的那部分參數。

57.5 線性迴歸複習

57.5.1 簡單線性迴歸

假設對於 \(n\) 名研究對象，我們測量個兩個觀測值 \((y_i, x_i)\)，那麼用線性迴歸模型來表示這兩個測量值估計的參數之間的關係就是：

\[ \begin{aligned} y_i & = \alpha + \beta x_i + \varepsilon_i \\ \text{Where } & \varepsilon_i \sim \text{NID}(0,1) \end{aligned} \]

或者用另一個標記法：

\[ Y_i | x_i \sim N(\alpha + \beta x_i, \sigma^2) \]

57.5.2 多元線性迴歸

如果預測變量有兩個或者兩個以上 \((x_i, \;\&\; z_i)\)，那麼描述這兩個預測變量和因變量之間的多元線性迴歸模型可以寫作：

\[ y_i = \alpha + \beta x_i + \gamma z_i + \varepsilon_i \]

此時， \(\beta\) 的含義是，當保持 \(z\) 不變時，\(x\) 每增加一個單位，\(y\) 的變化量。用這個模型，我們默認 \(z\) 保持不變的同時無論取值爲多少， \(x, y\) 之間的關係是不會變化的，我們用這個模型來調整 (adjust) \(z\) 的混雜效應 (confounding effect) (Section 30.5)。

當然我們也可以考慮當 \(z\) 取值不同時， \(x, y\) 之間的關係發生改變，只要在上面的多元線性迴歸方程中加入一個交互作用項即可 (Section 33)。

\[ y_i = \alpha + \beta x_i + \gamma z_i + \delta x_i z_i + \varepsilon_i \]

增加了交互作用項最大的變化是，\(x_i\) 的迴歸係數 \(\beta\) 的含義發生了改變：當且僅當 \(z = 0\) 且保持不變時，\(x\) 每增加一個單位，\(y\) 的變化量。如果 \(z = k \neq 0\) 且保持不變，那麼 \(x\) 每增加一個單位，\(y\) 的變化量則是 \(\beta + k\delta\)。

57.5.3 簡單線性迴歸的統計推斷

一個給定的樣本 \((y_i, x_i), i = 1, \cdots, n\) ，其對數似然方程是

\[ \ell(\alpha, \beta, \sigma^2 | \mathbf{y, x}) = -\frac{1}{2\sigma^2}\sum^n_{i=1}(y_i - \alpha - \beta x_i)^2 \]

分別對 \(\alpha, \beta\) 求微分之後可以獲得他們各自的 \(\text{MLE}\)：

\[ \begin{aligned} U(\alpha) & = \ell^\prime(\alpha) = \frac{1}{\sigma^2}\sum_{i=1}^n (y_i - \alpha - \beta x_i) \\ U(\beta) & = \ell^{\prime}(\beta) = \frac{1}{\sigma^2}\sum_{i=1}^n x_i(y_i - \alpha - \beta x_i) \\ U(\hat\alpha) & = 0 \Rightarrow \hat\alpha = \bar{y} - \hat\beta\bar{x} \\ U(\hat\beta) & = 0 \Rightarrow \hat\beta=\frac{\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^n(x_i-\bar{x})^2} = \frac{\sum x_iy_i - n\bar{x}\bar{y}}{\sum x_i^2 - n\bar{x}^2} \end{aligned} \]

注意到和線性迴歸章節中推導的過程不同 (Section 27.4.1)，當時我們用的是最小二乘法，這裏我們用的是光明正大的極大似然法，同時也證明了最小二乘法獲得的 \(\hat\alpha,\hat\beta\) 是他們各自的 \(\text{MLE}\)。

另外，殘差方差的 \(\text{MLE}\) 也可以用上面的方法推導出來，同樣和之前的方法 (Section 27.5) 做個對比吧：

\[ \begin{aligned} U(\sigma^2) & = \ell^\prime(\sigma^2) = -\frac{n}{2\sigma^2} + \frac{1}{2\sigma^4}\sum_{i=1}^n(y_i - \alpha - \beta x_i)^2 \\ U(\hat\sigma^2) = 0 & \Rightarrow \hat\sigma^2 = \frac{\sum_{i=1}^n(y_i - \hat\alpha - \hat\beta x_i)^2}{n} \end{aligned} \]

這個殘差方差的 \(\text{MLE}\) 其實不是一個無偏估計，它只是一個漸進無偏的估計 (需要除以 \(\frac{n-2}{n}\))，所以，當一個線性迴歸模型中有 \(p\) 個參數時：

\[ \hat\sigma^2 = \frac{\sum_{i=1}^n(y_i - \hat\alpha - \hat\beta_1 x_{i1} - \hat\beta_2 x_{i2}\cdots)^2}{n - p} \]

線性迴歸時殘差方差的檢驗統計量服從 \(F\) 分佈 (Section 29.2.6)。

57.6 GLM-Practical 01

57.6.1 建立似然方程

對下列不同的情形，寫下其

  1. 統計學模型
  2. 指明模型中的參數
  3. 推導該參數的對數似然方程

57.6.1.1 在 \(n\) 名對象中觀察到 \(k\) 個事件。

  1. 統計學模型: \(K\) 是隨機變量，指代事件的數量，\(K \sim \text{Bin}(n, \pi)\)。每個觀察個體中發生事件的概率相互獨立且相同。
  2. 模型參數: \(\pi\) 是模型參數，指代事件發生的概率。
  3. 對數似然的推導
  • 概率方程 (probability function):

\[ \text{Pr}(K = k) = \binom{n}{k}\pi^k(1-\pi)^{n-k}, k = 0,1,\cdots,n \]

  • 似然方程 (likelihood function):

\[ L(\pi|k) = \binom{n}{k}\pi^k(1-\pi)^{n-k}, 0<\pi<1 \]

  • 對數似然方程 (log-likelihood function):

\[ \ell(\pi|k) = k\log\pi + (n-k)\log(1-\pi) + \text{terms not involving } \pi, 0<\pi<1 \]

57.6.1.2 測量 \(n\) 名研究對象的總膽固醇濃度 (mmol/l)，已知人羣中總膽固醇的測量值呈正態分布且方差爲 \(4\) (mmol/l)2。

  1. 統計學模型: 用 \(Y_i\) 表示每個個體測量獲得的總膽固醇濃度值。它們是獨立同分布的隨機變量 (independent and indentically distributed, i.i.d. random variables): \(Y_i \sim N(\mu, 2^2 = 4)\)。
  2. 模型參數: 總體均值 \(\mu\)。
  3. 對數似然的推導:
  • 概率密度方程 (probability density function):

\[ \begin{aligned} f(y_1, \cdots, y_n) & = f(\mathbf{y}|\mu) = \prod_{i = 1}^n f(y_i | \mu) \\ & = \prod_{i=1}^n \frac{1}{\sqrt{2\pi2^2}}e^{-0.5(\frac{y_i-\mu}{2})^2} \\ & = [\frac{1}{\sqrt{2\pi2^2}}]^ne^{-0.5\sum_{i=1}^n(\frac{y_i-\mu}{2})^2} \\ & -\infty < y_i < + \infty \end{aligned} \]

  • 對數似然方程 (log-likelihood function):

\[ \ell(\mu|\mathbf{y}) = -\frac{1}{2\times2^2}\sum_{i=1}^n(y_i - \mu)^2 + \text{terms not involving } \mu, -\infty < \mu < + \infty \]

57.6.2 建立對數似然方程

對下列不同的情形，寫下其

  1. 參數的對數似然方程
  2. 推導極大似然估計
  3. 計算極大似然估計量
  4. 繪制對數似然方程的示意圖

57.6.2.1 在 10 名研究對象中觀察到 3 個事件

  1. 對數似然方程是

\[ \ell(\pi) = k\log\pi + (n-k)\log(1-\pi) \]

  1. 極大似然估計的推導

\[ \ell^\prime(\pi) = 0 \Rightarrow \frac{k}{\pi} - \frac{n-k}{1-\pi} = 0 \\ \Rightarrow \hat\pi = \frac{k}{n} \]

  1. 極大似然估計量 \(\hat\pi = 3/10 = 0.3\)

  2. 繪制對數似然方程的示意圖

pi <- seq(0,1, by = 0.0001)
likelihood <- 3*log(pi) + 7*log(1-pi)
plot(pi, likelihood, type = "l", ylim = c(-40, 0), frame.plot = TRUE,
     ylab = "log-likelihood(\U03C0)", xlab = "\U03C0" )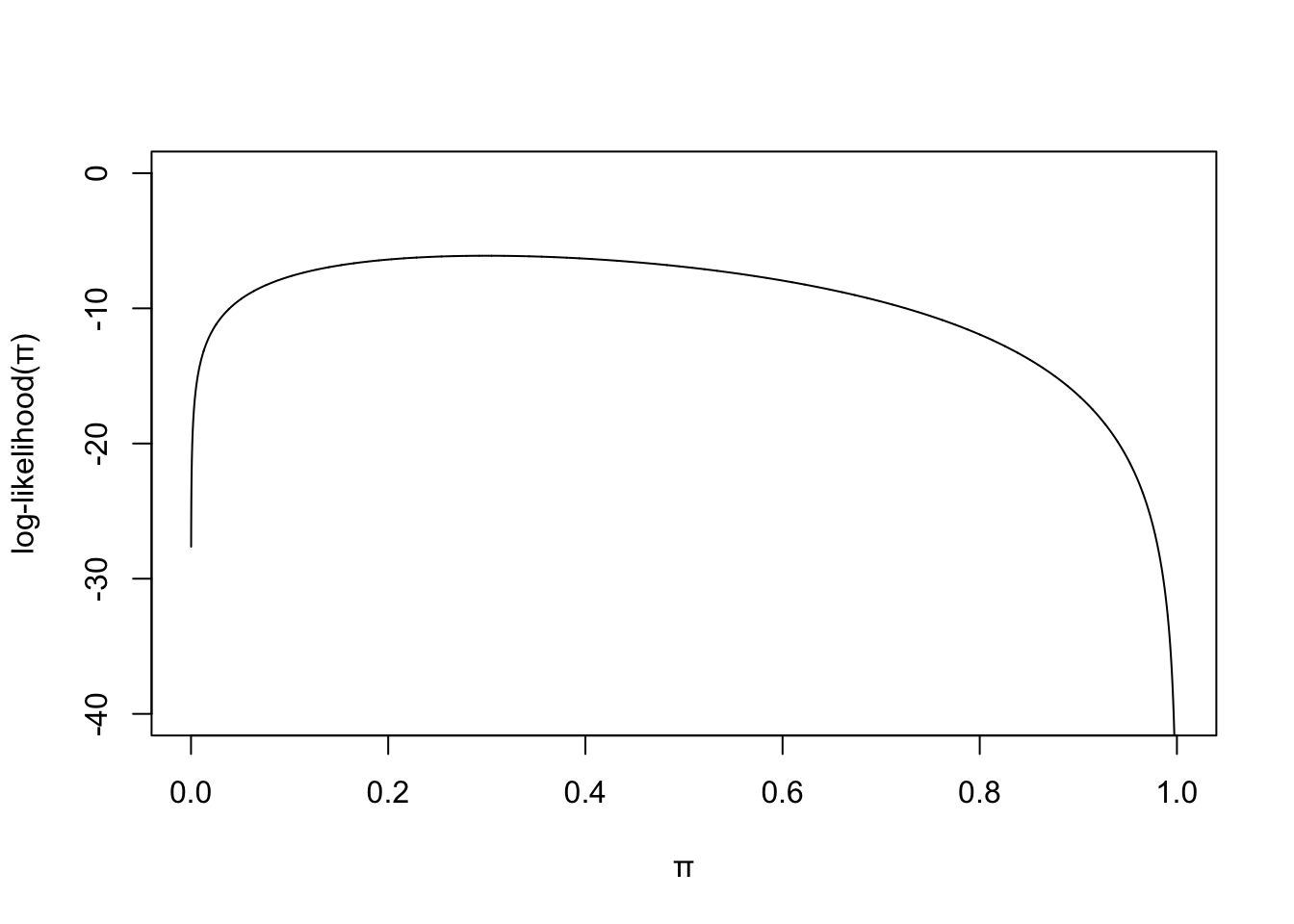
Log-likelihood for binomial model.

圖 57.1: Log-likelihood for binomial model.

57.6.2.2 10名研究對象測量的總膽固醇濃度分別是 6.0, 6.2, 6.8, 5.3, 5.9, 6.1, 6.0, 7.0, 5.9, 6.3。已知人羣中總膽固醇值服從方差爲 4 (mmol/l)2 的正態分布。

  1. 對數似然方程是:

\[ \begin{aligned} \ell(\mu) & = -\frac{1}{2\times2^2}\sum_{i=1}^{10} (Y_i - \mu)^2 \\ & = -\frac{1}{8}\sum_{i=1}^{10} (Y_i - \bar{y} + \bar{y} - \mu)^2 \\ & = -\frac{1}{8}\sum_{i=1}^{10} (\bar{y} - \mu)^2 \\ & = -\frac{10}{8}(\bar{y} - \mu)^2 \end{aligned} \]

  1. 極大似然估計，和極大似然估計量是:

\[ \ell^\prime(\mu) = 0 \Rightarrow \hat\mu = \bar{y} = 6.15 \]

  1. 繪制對數似然方程的示意圖
mu <- seq(5,7, by = 0.0001)
likelihood <- -(5/4)*(6.16-mu)^2
plot(mu, likelihood, type = "l", ylim = c(-1.8, 0), frame.plot = TRUE,
     ylab = "log-likelihood(\U03BC)", xlab = "\U03BC" )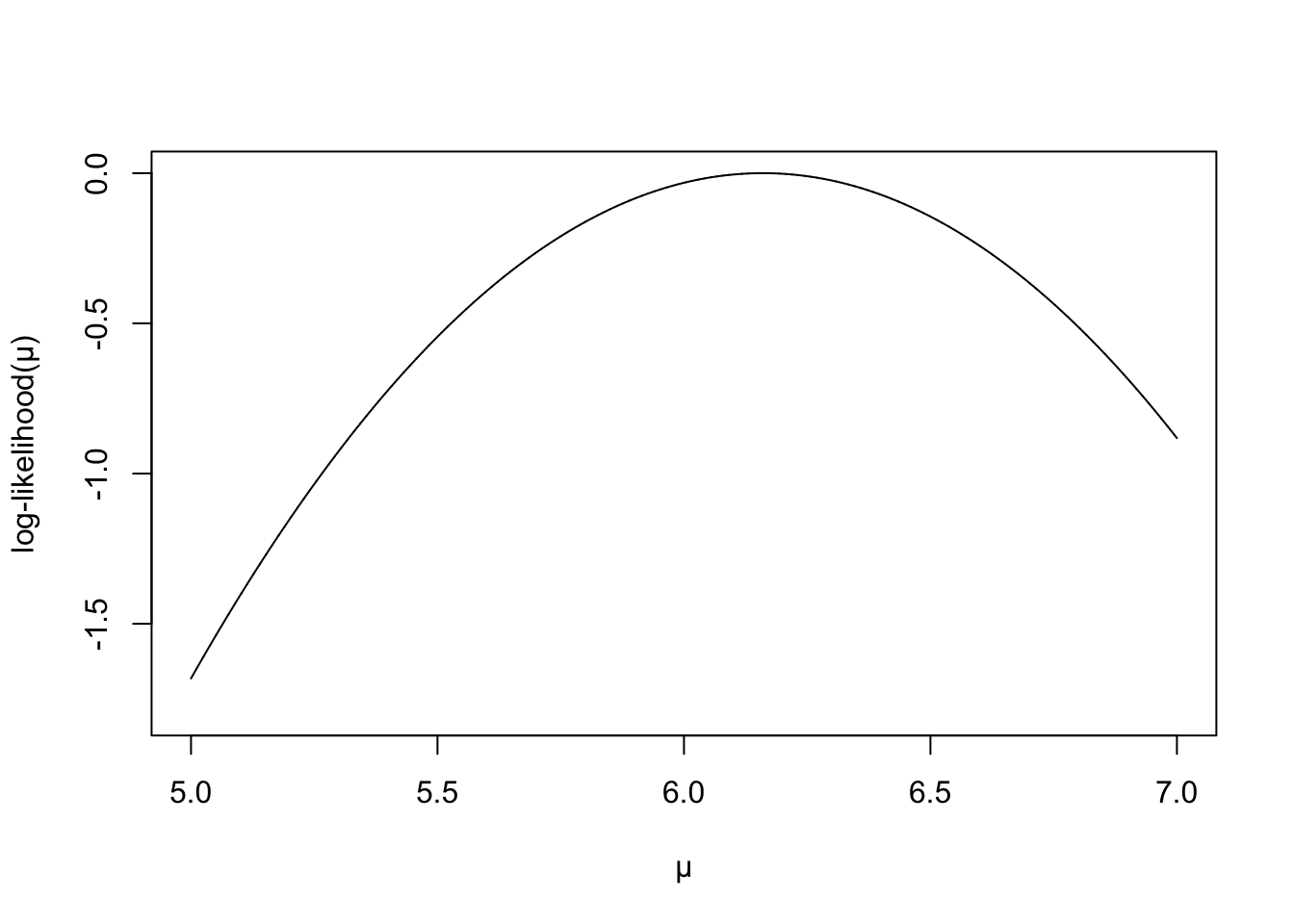
Log-likelihood for normal model

圖 57.2: Log-likelihood for normal model

57.6.3 線性回歸模型

某項RCT臨牀實驗的目的是比較注射嗎啡和安慰劑哪個對患者的精神醫學指徵的改變更加有效。每個實驗組隨機分配到24名患者，精神醫學指徵使用某種心理調查問卷，問卷有七道題，患者七道題的總得分被用於評價其精神醫學指徵，的分越高，指徵越明顯。下表是這兩組患者在注射相應藥物兩小時之後答題的的分:

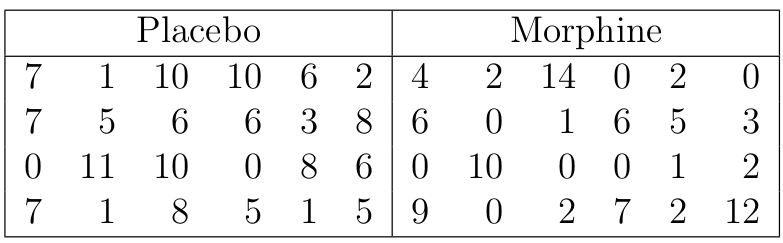
Mental activity scores recorded 2 hours after injection of the drug.

圖 57.3: Mental activity scores recorded 2 hours after injection of the drug.

下面是 STATA 的計算結果，

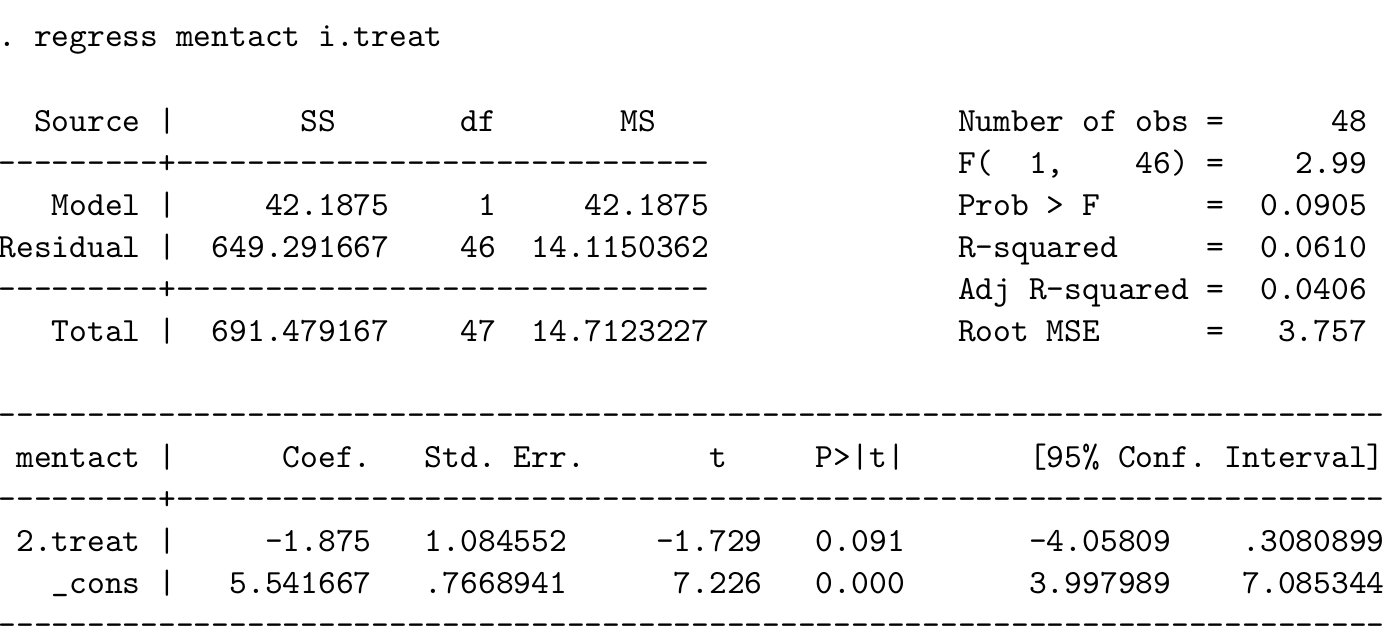
  1. 寫下該模型的數學表達式，陳述該模型中用到的所有假設和前提條件。用手頭的計算器手動計算該簡單線性回歸模型的截距和斜率，確定你的結果和STATA的結果是一樣的。

\(Y_i\) 用來表示第 \(i\) 名對象的精神醫學指徵問卷的得分。該模型可以寫作:

\(Y_1, Y_2, \cdots, Y_{48}\) 是 48 個獨立同分布的隨機變量，且 \(Y_i \sim N(\mu, \sigma^2)\) \[ y_i = \alpha + \beta x_i \text{ for } x_i = \left\{ \begin{array}{ll} 0 \text{ placebo}\\ 1 \text{ morphine}\\ \end{array} \right. \]

從表格數據中可得 \(\bar{x} = 0.5, \sum x_i^2 = 24, \bar{y}=4.604, \sum x_iy_i=88\)，利用之前 57.5.3 復習的簡單線性回歸公式:

\[ \hat\alpha = 5.542 \\ \hat\beta = -1.875 \]

  1. 解釋截距和斜率的實際意義:
  • \(\hat\alpha\) 是安慰劑組的平均精神醫學指徵得分;
  • \(\hat\beta\) 是注射嗎啡組和安慰劑組兩組之間得分均值之差。
  1. 實驗研究同時還測量了兩組在注射藥物之前的精神醫學指徵得分，下面是在 STATA 裏對該數據進行擬合的另一個模型。其中 prement 是藥物注射前得分的變量:

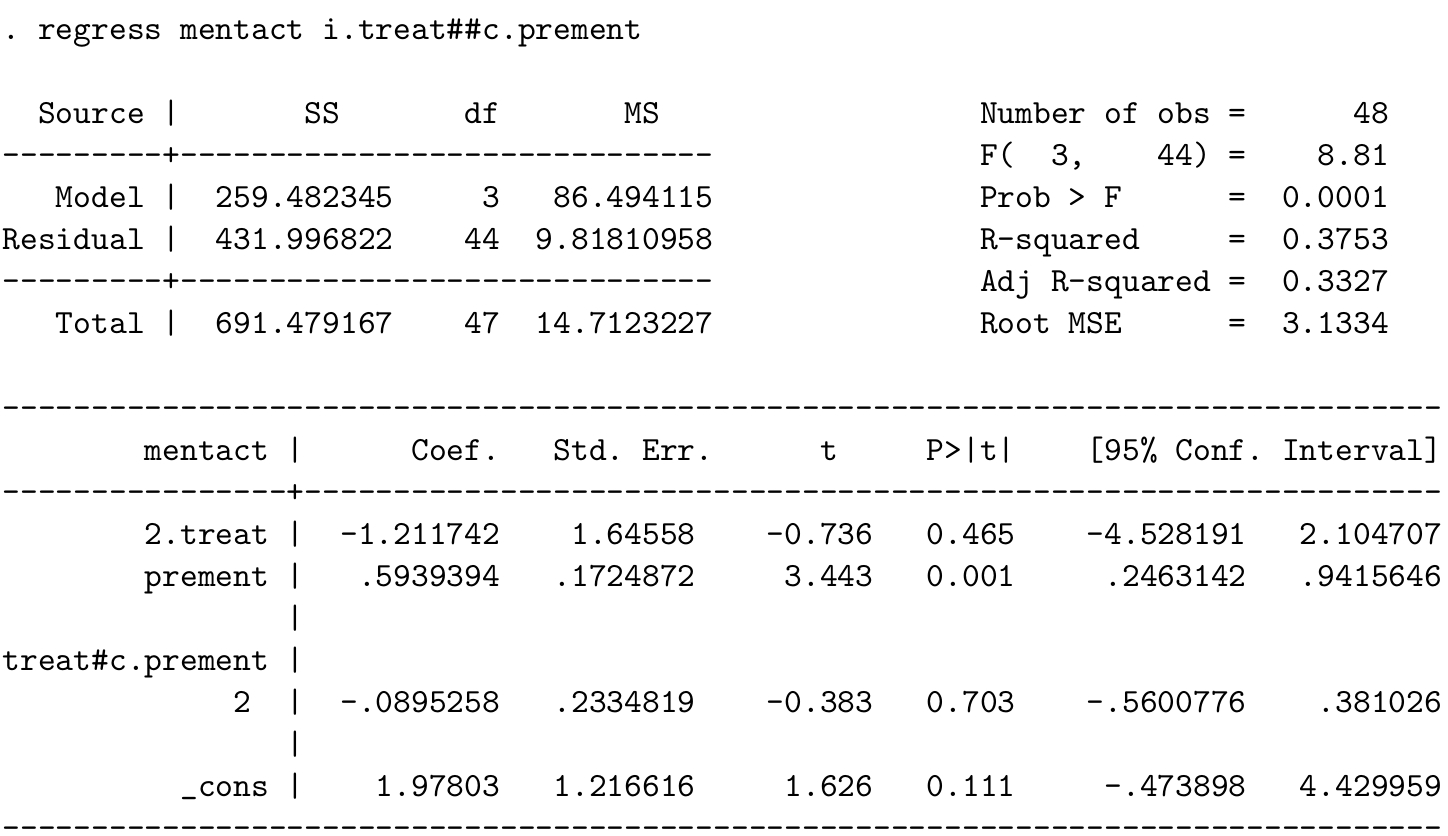
  1. 寫下這個模型的數學表達式，並且解釋你會用怎樣的方法求各個參數的 MLE。

\[ y_i = \beta_0 + \beta_1 x_i + \beta_2 z_i + \beta_{12}x_iz_i \\ \text{ for } x_i = \left\{ \begin{array}{ll} 0 \text{ placebo}\\ 1 \text{ morphine}\\ \end{array} \right. \]

該模型的對數似然方程是

\[ \ell(\beta_0, \beta_1, \beta_2, \beta_{12} | \mathbf{y, z, x}) = -\frac{1}{2\sigma^2}\sum_{i=1}^{48}(y_i - \beta_0 - \beta_1x_i - \beta_2z_i - \beta_{12}x_iz_i)^2 \]

把上面的對數似然方程等於零以後依次對 \(\beta_0, \beta_1, \beta_2, \beta_{12}\) 求偏微分即可求得各自的 MLE。

  1. 解釋各參數估計的實際意義
  • \(\hat\beta_0 =\) _cons \(=1.978\) 是當且僅當治療前得分爲零時，模型對安慰劑組得分均值的估計;
  • \(\hat\beta_1 =\) 2.treat \(=-1.212\) 是當且僅當治療前得分爲零時，嗎啡組和安慰劑組之間得分均值之差;
  • \(\hat\beta_2 =\) prement \(=0.594\) 是對照組中，治療前得分每增加一個單位，治療後得分的變化;
  • \(\hat\beta_{12} =\) 2.treat#c.prement \(=-0.0895\) 是嗎啡組和安慰劑組兩組之間回歸斜率之差，也就是說 \[\hat\beta_2 + \hat\beta_{12} = 0.505\] 是嗎啡組中，治療錢得分沒增加一個單位，治療後得分的變化。

57.6.4 似然比檢驗，Wald 檢驗，Score 檢驗

從服從正態分布 \(N(\mu, 1)\) 的總體中抽樣 \(n\) 個樣本，他們相互獨立同分布 (i.i.d)。推導用這個模型時的三種檢驗方法的檢驗統計量，證明在此特殊情況下，三種檢驗方法的檢驗統計量完全一致。

該數據的對數似然是

\[ \ell(\mu) = -\frac{1}{2}\sum_{i=1}^n(y_i - \mu)^2 \]

  1. 似然比檢驗 likelihood ratio test

\[ \begin{aligned} -2llr & = -2(\ell(\mu_0 - \ell(\hat\mu))) \\ & = -2(-\frac{1}{2}\sum_{i=1}^n(y_i - \mu_0)^2 + \frac{1}{2}\sum_{i=1}^n(y_i - \bar{y})^2) \\ & = \sum_{i=1}^n[(y_i - \mu_0)^2 - (y_i - \bar{y})^2] \\ & = \sum_{i=1}^n(y_i^2 + \mu_0^2 - 2\mu_0y_i - y_i^2 - \bar{y}^2 + 2\bar{y}y_i) \\ & = n(\mu_0^2 - 2\mu_0\bar{y} + \bar{y}^2) \\ & = n(\bar{y} - \mu_0)^2 \end{aligned} \]

  1. Wald 檢驗:

對數似然的一階導數和二階導數分別是:

\[ \ell^\prime = -\frac{1}{2}\sum_{i=1}^n-2(y_i-\mu) = \sum_{i=1}^n(y_i - \mu) \\ \ell^{\prime\prime} = -n \]

所以，Fisher information \(S^2 = n^{-1}\)，\(M = \hat\mu = \bar{y}\)，

\[ \begin{aligned} W^2 & = (\frac{M - \theta_0}{S})^2 \\ & = (\frac{(\bar{y} - \mu_0)^2}{n^{-1}}) \\ & = n(\bar{y} - \mu_0)^2 \end{aligned} \]

  1. Score 檢驗

\[ \begin{aligned} \frac{\ell^\prime(\mu_0)^2}{-\ell^{\prime\prime}(\mu_0)} & = \frac{(n\bar{y} - n\mu_0)^2}{n} \\ & = n(\bar{y} - \mu_0)^2 \end{aligned} \]

所以，在方差已知，均值未知，總體服從正態分布的數據條件下，三種檢驗方法獲得的實際檢驗統計量是完全一致的。