第 105 章 非參貝葉斯入門
- If I’m doing an experiment to save the world, I better use my prior.
- Andrew Gelman
這裏的筆記來自於下列參考書的閱讀心得,思考,及其中的練習:Bayesian nonparametric data analysis (Müller et al. 2015), by Peter Müller, Fernando Andres Quintana, Alejandro Jara, Tim Hanson.
統計學問題,通常可以使用概率模型來描述。這句話的真實意涵是,我們觀察到的數據,其實是由一組我們想象的 (envisioned) 隨機變量 \(y_1, \dots, y_n\) 實現的。這一組隨機變量可以對應到我們收集的第 \(i\) 個實驗單元 (experimental unit),而衆多的實驗單元又組成了 \(n\) 個來自總體的樣本。一個最常見的假設是,\(y_n\) 是從某個概率分佈 \(G\) 中採集而來,它們之間相互獨立 (drawn independently)。那麼我們關心的統計學問題,就起源於這個概率分佈 \(G\) 本身的不確定性 (uncertainty)。我們使用 \(g\) 表示該概率分佈的概率密度函數 (p.d.f, probability density function)。當 \(g\) 已知是屬於某個分佈家族 (family of distribution) \(\mathcal{G} = \{ g_\theta : \theta \in \Theta \}\) 的一員 \(g_\theta\),且該概率分佈函數的特徵參數可以用 \(\theta\) 表示,\(\theta\) 是該分佈家族中會使用到的特徵參數集合 \(\Theta\) 的一個子集時,我們就有了一個完整的統計學模型。
統計學模型本身,可以由多個特徵參數組成的向量來描述,通常這個特徵參數的向量中的元素是有限個的 (finite-dimensional),我們稱這樣的統計學模型爲,參數模型 parametric model。這樣的參數統計學模型可以用數學語言描述爲:\(\mathcal{G} = \{ g_\theta : \bar{\theta} \in \Theta \subset \mathbb{R}^p \}\)。那麼統計分析的目的,就轉化成使用樣本數據尋找一個合理的參數估計值 \(\bar{\theta}\),或者至少找到 \(\Theta\) 中包含 \(\bar{\theta}\) 的一部分子集。可是,在許多情況下,給統計學模型人爲地施加過多的約束,特別是限制它爲某一類分佈族等參數被強制爲某些特殊形態時,我們的模型推斷也就被人爲地施加了範圍和限制。於是,有智者認爲,我們應該放鬆這樣的模型參數的前提條件等限制 (relax the parametric assumptions),從而允許統計學模型有更大的靈活性 (flexibility),和穩健性 (robustness),且降低模型被錯誤描述的可能性 (mis-specification)。爲了解除參數的限制,我們考慮的統計學模型應該被賦予極大的靈活性,也就是它所屬的那個分佈家族的概率密度函數,可以描述它的參數個數限制應當被放寬,以至於可以允許有無限多個參數 \(\bar{\theta}\) (finite dimensional space)。
Example 105.1 密度估計 (density estimation)
思考這樣一個簡單的隨機樣本 \(y_i | G \stackrel{i.i.d}{\sim} G, i = 1, \dots, n\)。這個樣本可能來自一個未知的分佈\(G\)。有的人在分析這個樣本數據的時候,可能就選擇把這個未知的分佈限制爲一個正(常)態分佈,即 \(\mathcal{G} = \{\mathbf{N}(\theta, 1): \theta \in \mathbb{R}\}\)。那麼圖 105.1 (a) 則展示了使用正(常)態分佈對該簡單隨機樣本做的推斷結果,該推斷基於的假設就是該樣本\(y_1, \dots, y_n\)是隨機採集自一個正(常)態分佈。那麼很顯然,這樣的估計和假設雖然可能是沒有太大問題的,但是這個未知的分佈\(G\)由於受制於正(常)態分佈這樣一個假設,就不可能允許有多個峯值 (multi-modality),或者偏度 (skewness)。與之形成對比的是,圖 105.1 (b) 則是使用了非參數模型 (nonparametric model),並且用概率模型\(\pi\)作爲該未知分佈 \(\mathcal{G}\) 的先驗概率模型 (prior probability model) 對該樣本數據進行的推斷示例。圖 105.1 (b) 使用的是一種叫做狄雷克雷過程 (Dirichlet process) 的方法做先驗混合概率 (mixture prior),然後通過非參數貝葉斯 (Bayesian Nonparametric, BNP) 作出的較爲靈活的推斷。圖中的點線,對應的是採集的事後樣本 (posterior draws)。
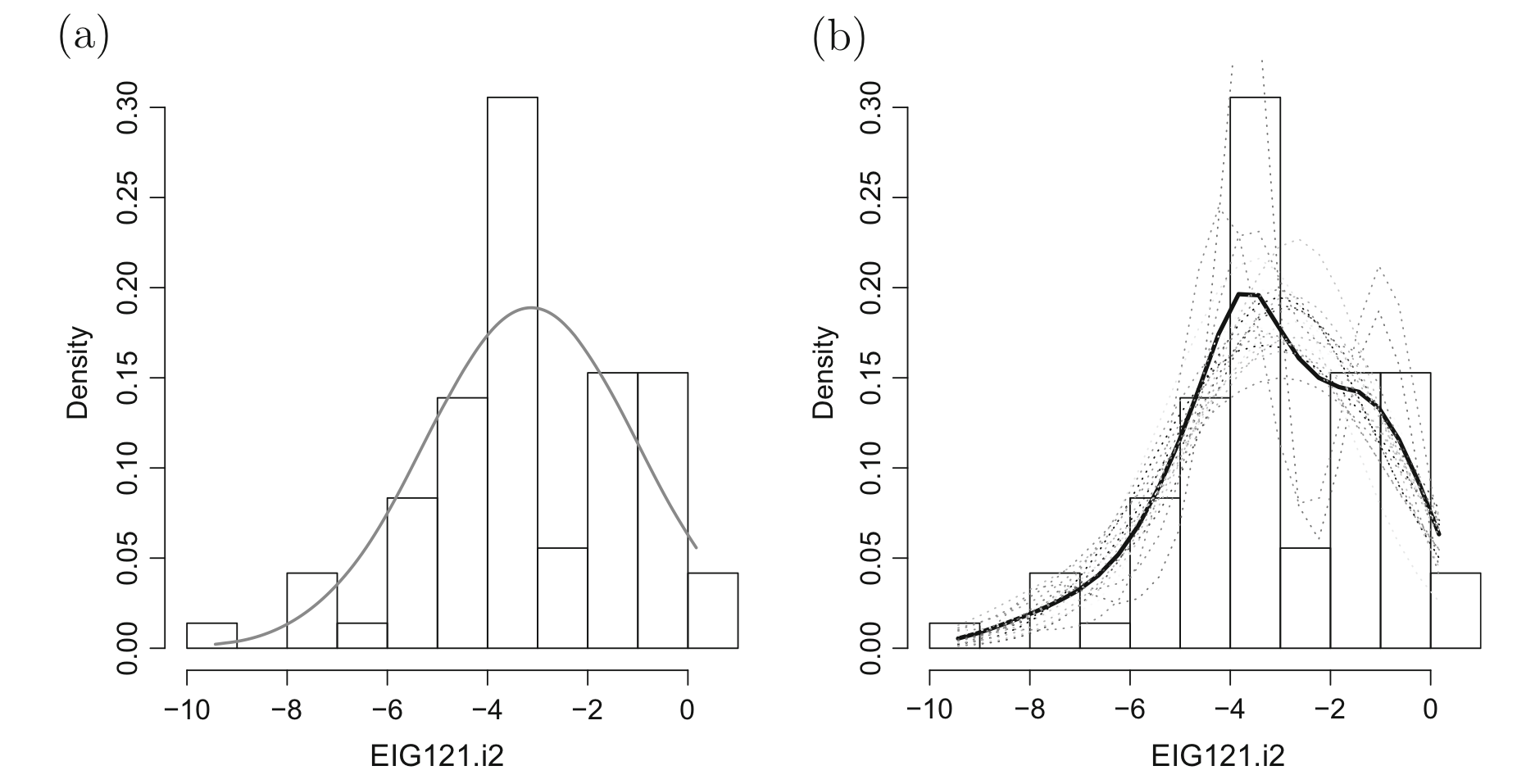
圖 105.1: Inference on the unknown distribution \(G\) under a parametric model (a) and nonparametric model (b). The historgram of the observed data is also displayed. The dotted line in (b) correspond to posterior draws.
在示例 105.1 中,那個未知的,有無限維度(參數個數不加限制的)的就是 \(G\) 本身。另一個較爲容易理解的無限維度參數空間 (infinite-dimensional parameter space) 的例子其實是一条定義在長度不限的實線上的連續函數 (continuous function defined on the real line): \(S = \{ m(z) : z \in \mathbb{R}, m(\cdot) \text{ is a continuous function}\}\)。例如可以是一條均值未知的 (\(m(z)\)) 回歸直線。允許了無限維度參數的模型被叫做非參數模型 (non-parametric models)。你可能會看見有人把這樣的無限維度參數 \(\bar{\theta}\) 寫作:\((\bar{\theta}_1, \bar{\theta}_2)\),其中 \(\bar{\theta}_1\) 是 \(q\) 維度參數向量,\(\bar{\theta}_2\) 是無限維度參數向量。這樣的模型,由於同時包括參數部分和非參數部分又被稱作半參數 (semi-parametric) 模型。典型的半參數模型,我們熟悉的有比例風險模型 (proportional hazards model) (Chapter 88)。比例風險模型最常見用於對生存時間 \(T\) 的分析。假如該模型中我們希望加入考慮的參數向量是 \(\bar{z}\),那麼下式用於表示條件風險率 (conditional hazard rate):
\[ \begin{equation} \lambda(t | \bar{z}) = \lim_{h \rightarrow 0} \{ \frac{p(t \leq T < t + h | T \geq t, \bar{z})}{h} \} \tag{105.1} \end{equation} \]
比例風險模型認爲:
\[ \lambda(t | \bar{z}) = \lambda_0 (t) \exp(\bar{z}^\prime \bar{\beta}) \]
其中,\(\lambda_0(\cdot)\) 是基線風險函數 (baseline hazard function),\(\bar{\beta}\) 是 \(q\) 維的回歸係數組成的向量。在經典的半參數版本的Cox風險比例回歸模型中,這個基線風險函數是被忽略掉,不進行估計的。所以這個函數就可以是任意的關於時間 \(t\) 的正函數,它就是一個無限維度的函數。所以,使用比例風險函數的模型,它的參數集合可以用 \(\bar\theta = (\bar{\beta}, \lambda_0)\) 表示。事實上,生存數據本身的概率密度函數 \(f_T\) 和風險函數之間是有關係的:
\[ f_T(t | \bar{z}) = \lambda_0 (t) \exp(z^\prime \bar{\beta}) \exp\{ -\exp(z^\prime \bar{\beta}) \int_0^t \lambda_0(u) du \} \]
於是,上述概率密度函數中我們關心的參數就有兩個部分:\(\bar\theta_1 = \bar{\beta}\),和 \(\bar\theta_2 = \lambda_0\),那麼把這兩部分合起來就可以寫作 \(\bar\theta = (\bar\theta_1, \bar\theta_2) \in \mathbf{\Theta} = \mathbb{R}^q \times \mathcal{S}\)。其中 \(\mathcal{S}\) 是指代所有可能的在正實數空間 \(\mathbb{R}^+\) 裏的無限維度的非負函數。
Example 105.2 口腔癌例子
數據是源於 (Klein and Moeschberger 2006) Section 1.11。該數據報告了 80 名口腔癌患者的生存時間。患者中有染色體數量異常 (aneuploid) 和染色體數量二倍體正常 (diploid)。我們定義 \(z_i \in \{0, 1\}\) 爲指示患者是否是染色體異常的變量。之後使用比例風險函數 (105.1) 做生存時間的推斷,且對本來不估計的基線風險 \(\lambda_0\) 使用非參貝葉斯的方法做推斷。圖 105.2 就展示了染色體異常與否的兩組患者的風險度曲線。我們使用了 penalized B-spline 作爲 \(\log\{\lambda_0(\cdot)\}\) 的先驗概率,在 R2BayesX 的R包的輔助下完成。
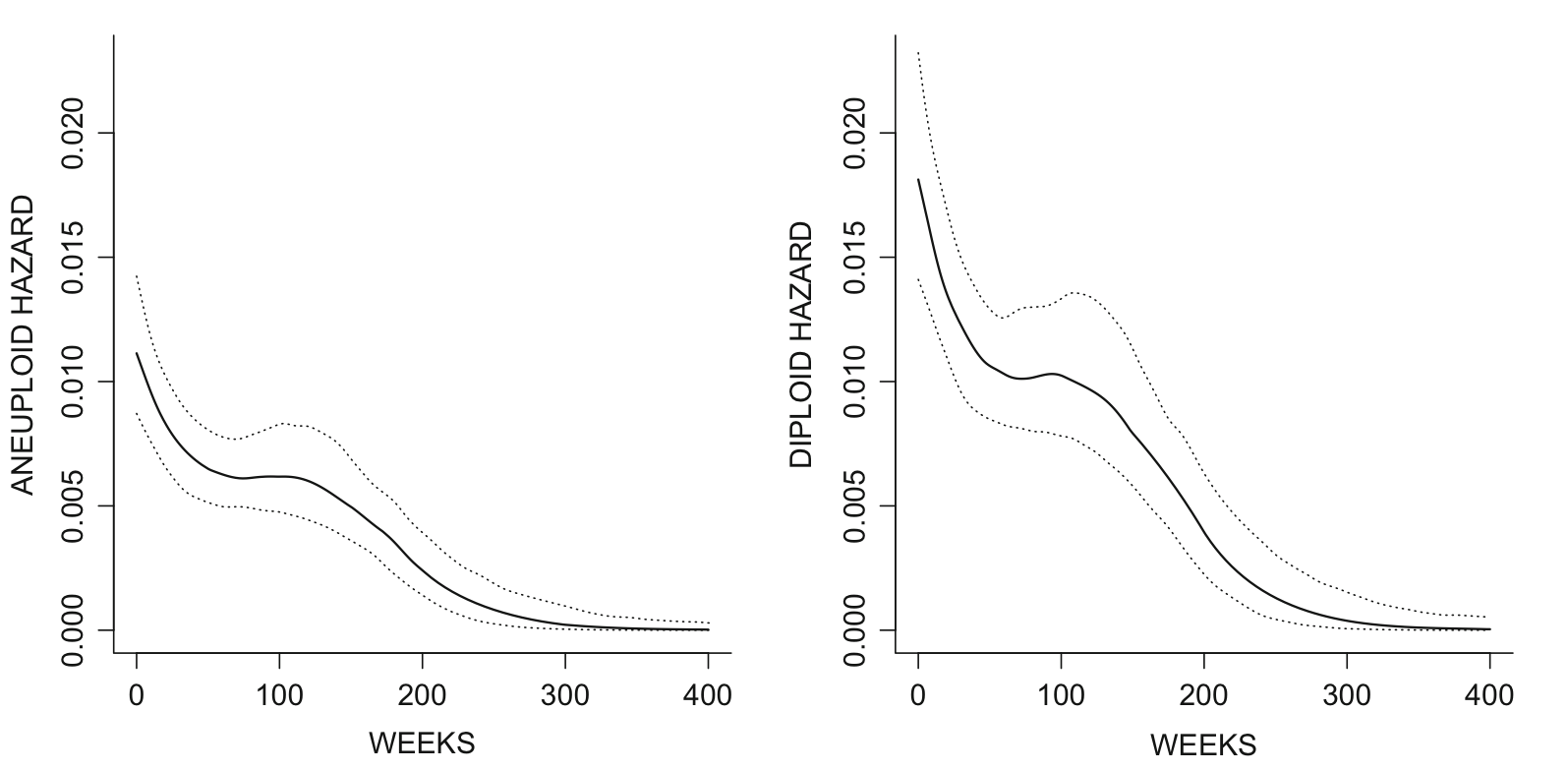
圖 105.2: Hazard curves for aneuploid and diploid groups under the proportional hazard model with point-wise 50% CIs.
爲了能夠在非參數模型中完成貝葉斯推斷,我們需要爲概率模型補充一個無限維度參數的先驗概率。這樣的先驗概率被叫做非參貝葉斯先驗概率 (BNP prior)。也就是說,我們定義BNP先驗概率作爲無限維度參數的概率模型,這樣的推斷過程被稱爲 BNP 模型。這也就是非參數貝葉斯推斷和經典非參數推斷之間的不同點。無論是 BNP 還是經典非參數推斷,都設定了無限維度參數用來描述我們的樣本所代表的那個概率模型。二者最大的不同點是,貝葉斯推斷是把先驗概率分佈的參數給無限維度化。這樣BNP推斷就擁有了能夠用完整的概率描述法,解釋所有相關不確定性的潛力。經典的非參數法,則是把無限維度的參數當作可以忽略的“雜音”參數,通過一些巧妙的手段避開對他們直接進行估計,而且把重點放在估計那些有限的,我們關心的參數上去。