第 108 章 Graphical Models 因果推斷的圖形模型
條件可置換性 (conditional exchangeability) 是因果推斷中最重要的前提假設。
\[ Y(x) \perp \!\!\! \perp X|\mathbf{C}, \forall x \]
當你的變量太多的時候,用圖形來表示變量之間的條件關系顯得十分直觀。有向無環圖 (Directed acyclic graphs, DAG) 就是能夠幫助我們理解變量之間條件獨立性關系的好工具。
108.1 統計學中的有向無環圖
Definition 108.1 DAG, 是一種包括了多個節點 (nodes),並且用箭頭直線連接這些節點的一種示意圖,值得注意的是,我們用的 DAG 示意圖中,沒有閉環 (也就是沒有哪個節點會隨着箭頭回到該節點本身成爲一個閉環,所以叫做有向無環圖)。且,DAG示意圖中也沒有雙向箭頭鏈接任何兩個節點。
統計學中,DAG 用來表示一系列變量的聯合分布 (joint distribution),它的箭頭指向表示了不同變量之間的向量關系。(DAGs are used to represent the factorisation of a joint distribution.) 如果一組變量組成向量 \(\mathbf{V}=(V_1, V_2, V_3, V_4, V_5, V_6)\),且這些變量之間的聯合分布關系是這樣子:
\[ \begin{aligned} &p_\mathbf{V}(\mathbf{v}) = \\ &\;p_{V_1}(v_1)p_{V_2}(v_2)p_{V_3|V_1,V_2}(v_3|v_1,v_2)p_{V_4|V_1,V_3}(v_4|v_1,v_3)p_{V_5|V_1,V_2}(v_5|v_1, v_2)p_{V_6|V_5}(v_6|v_5) \end{aligned} \]
那麼這些變量之間關系對應的 DAG 圖就是這樣子:
g <- dagitty('dag {
V6 [pos="2,0"]
V4 [pos="1,-1"]
V5 [pos="1,1"]
V2 [pos="-1,-1"]
V3 [pos="-1,1"]
V1 [pos="-2,0"]
V1 -> V4
V1 -> V5 -> V6
V1 -> V3 -> V4
V2 -> V3 -> V4
V2 -> V5 -> V6
}')
plot(g)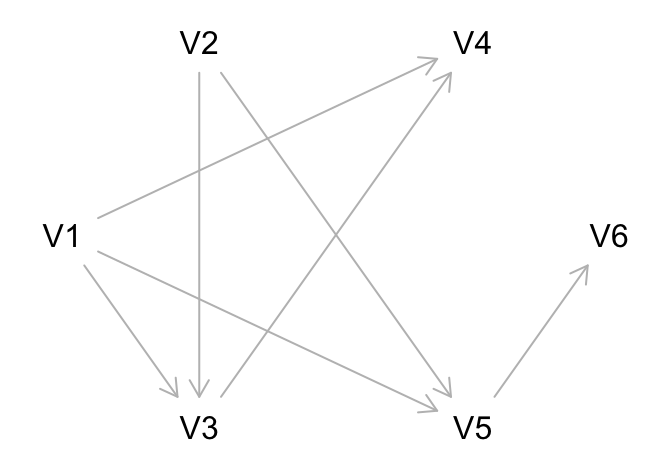
圖 108.1: Example of a DAG
上面長長的因子化 (factorisation) 公式可以簡略爲:
\[ p_{\mathbf{V}}(\mathbf{v}) = \prod_jp_{V_j|S_j}(v_j|s_j) \]
其中 \(S_j\) 是 \(V_j\) 的子集,在DAG圖中,我們可以添加從 \(V_k\) 到 \(V_j\) 箭頭的充分且必要條件是 \(V_k \in \mathbf{S}_j\)。
108.1.1 DAG 和條件獨立性 conditional independence
DAG 圖包含了變量之間的條件獨立性關系。如果 \(V_k\) 到 \(V_j\) 沒有箭頭,意味着這兩個變量在所有其他有指向 \(V_j\) 箭頭的變量的條件下,互相獨立:
\[ V_4 \perp \!\!\! \perp V_2 | V_1, V_3 \]
108.1.2 DAG 圖的術語
Definition 108.2 父與子 parent and child: \(V_i\rightarrow V_j\),那麼 \(V_i\) 是 \(V_j\) 的父,\(V_j\) 是 \(V_i\) 的子。圖108.1中 \(V_2\) 是 \(V_5\) 的父,\(V_5\) 是 \(V_2\) 的子。
Definition 108.3 通路 path: 從節點 \(V_i\) 到另一個節點 \(V_j\) 如果可以用 DAG 箭頭 (方向可左可右) 從頭到尾連接起來,成爲一個通路。\(V_i, V_{k_1}, \cdots ,V_{k_n}, V_j\) 之間如果有通路,那麼這個通路上的每兩個變量之間都有一個箭頭連接 (無論哪個方向)。圖 108.1 中 \(V_1\rightarrow V_3 \leftarrow V_2 \rightarrow V_5\) 是一條從 \(V_1\) 到 \(V_5\) 的通路。
Definition 108.4 有向通路 directed path: 從節點 \(V_i\) 到節點 \(V_j\) 之間如果有通路,且箭頭的方向只有從左往右,那麼這個通路被叫做有向通路。圖 108.1 中 \(V_1\rightarrow V_5 \rightarrow V_6\) 是一條從 \(V_1\) 到 \(V_6\) 的有向通路。
Definition 108.5 祖先與後代 ancestor and descendant: 如果 \(V_i\) 和 \(V_j\) 之間有一條有向通路,那麼我們說 \(V_i\) 是 \(V_j\) 的祖先,\(V_j\) 是 \(V_i\) 的後代。圖 108.1 中 \(V_2\) 是 \(V_6/V_5\) 的祖先,\(V_6/V_5\) 是 \(V_2\) 的後代。
Definition 108.6 對撞因子 collider: 如果一條通路上的某個變量 \(V_{K_i}\) 有左右兩個箭頭同時指向它本身,那麼\(V_{K_i}\) 被叫做對撞因子。圖 108.1 中 \(V_1\rightarrow V_3 \leftarrow V_2\),的通路上 \(V_3\) 是一個對撞因子。
108.1.3 阻斷通路 blocking paths
Definition 108.7 當 \(\mathbf{Z}\in\mathbf{V}\) 時,如果一條通路 \(p\) 上存在一個節點 \(W\) 滿足這兩個條件中的一個: (1) \(W\) 是通路 \(p\) 上的一個對撞因子,且 \(W\) 和它的任何後代都 \(\notin \mathbf{Z}\)。(2) \(W\) 不是通路 \(p\) 上的對撞因子,且 \(W\in\mathbf{Z}\)。我們說 \(\mathbf{Z}\) 阻斷了通路 \(p\)。
108.1.4 以對撞因子爲條件 conditioning on a collider
如下圖 108.2 所示,\(V_3\) 取決於 \(V_1, V_2\),且 \(V_1, V_2\) 互相獨立。那麼給定了 \(V_3\) 之後 \(V_1, V_2\) 其實就變成了條件依賴的關系 (conditionally dependent)。盡管 \(V_1, V_2\) 這兩個變量之間是邊際獨立 (marginally independent) 的關系。
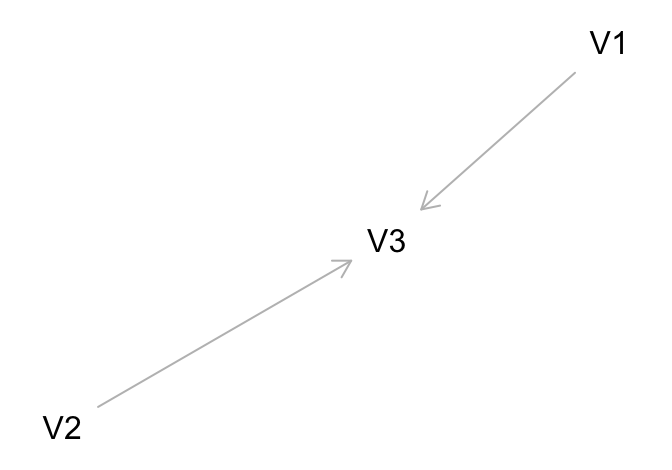
圖 108.2: Conditioning on a collider
108.2 以非對撞爲條件 conditioning on a non-collider
如果 \(V_1,V_2\) 同時取決於 \(V_3\):
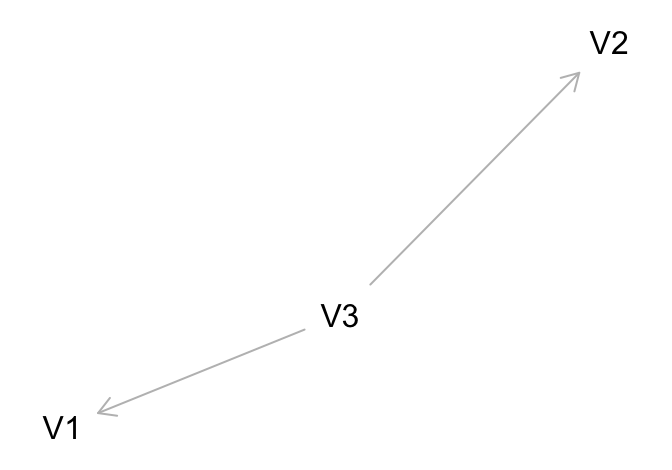
圖 108.3: Conditioning on a non-collider (1)
那麼此時 \(V_1,V_2\) 的關系是邊際依賴 (marginally dependent),但是以 \(V_3\) 爲條件獨立 (conditionally independent)。
假設三個變量之間的關系又變成: \(V_3\) 取決於 \(V_1\),\(V_2\) 取決於 \(V_3\):
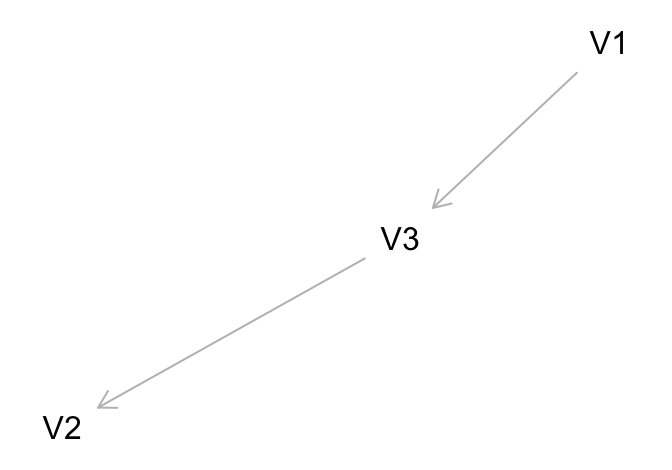
圖 108.4: Conditioning on a non-collider (2)
類似地,此種情形底下, \(V_1,V_2\) 的關系也是邊際依賴 (conditionally dependent),但是以 \(V_3\) 爲條件獨立 (conditionally independent)。
108.2.2 D 分離 d-separation
Definition 108.8 一組變量組成的向量 \(\mathbf{V}\),如果它的三個沒有交集的子集向量 \(\mathbf{X,Y,Z}\) 之間中的一個 \(\mathbf{Z}\) 把 \(\mathbf{X}\) 到 \(\mathbf{Y}\) 的通路全部阻斷 (block),我們說 \(\mathbf{Z}\) 把 \(\mathbf{X}\) 中的任何一個節點到 \(\mathbf{Y}\) 中任何一個節點 d 分離了 (d-seperate)。
Example 108.1 圖 108.4 中,\(V_2\) 是否阻斷了 \(V_3\) 到 \(V_6\) 的通路呢?
從 \(V_3\) 到 \(V_6\) 的通路一共有如下幾條:
\[ \begin{aligned} 1.& V_3 \leftarrow V_1 \rightarrow V_5 \rightarrow V_6 \\ 2.& V_3 \leftarrow V_2 \rightarrow V_5 \rightarrow V_6 \\ 3.& V_3 \rightarrow V_4 \leftarrow V_1 \rightarrow V_5 \rightarrow V_6 \end{aligned} \]
其中,第 2,3 條通路,是被 \(V_2\) 阻斷了的,但是第 1 條沒有被 \(V_2\) 阻斷。 因此,我不能說 \(V_2\) 把 \(V_3\) 到 \(V_6\) 之間的全部通路阻斷 (d-分離,d-separation)。
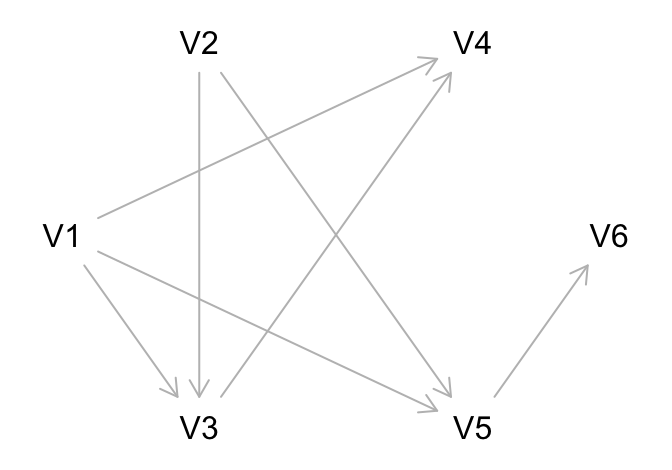
圖 108.5: Example of a DAG
Theorem 108.1 D分離和條件獨立性: 如果 \(\mathbf{X, Y, Z}\) 之間互無交集,且 \(\mathbf{Z}\) d 分離了從 \(\mathbf{X}\) 到 \(\mathbf{Y}\) 之間的所有通路那麼有:
\[\mathbf{X}\perp \!\!\! \perp\mathbf{Y|Z}\]
根據 D 分離的定義來看,通過 DAG 圖,可以直觀地分析一組變量和另一組變量在已第三組變量爲條件的基礎上通路的變化和變量之間的獨立性。以某組變量爲條件之後,很可能阻斷了某些通路的同時,又解鎖了某些通路,當殺死一些通路的同時,可能建立起其他變量之間的聯系。這是一個有內在邏輯聯系的關系網絡。
變量之間通路的打開,阻斷,d 分離過程,用手繪制當然可行,但是變量如果很多,這個過程就顯得太過於繁瑣,幸好我們已經有了完美的解決方案,可以使用在線DAG工具: www.dagitty.net。