第 25 章比較 Comparisons

本章暫且只討論兩組之間的比較 (均值，方差，百分比)；
本章也只討論兩種類型的變量，連續型和二分類型變量；
本章會介紹點估計 (point estimation)，信賴區間計算 (confidence intervals)，假設檢驗 (hypothesis testing)。

25.1 比較兩個均值 comparing two population means

25.1.1 當方差已知，且數據服從正態分佈 Z-test

令 \(Y_{1i} (i=1,2,\cdots, n_1); Y_{2i} (i=1,2,\cdots, n_2)\) 表示兩個獨立且隨機的變量，他們來自兩個人羣 (1 和 2)，且各自的人羣均值爲 \(\mu_k\)，方差爲 \(\sigma_k^2\)：

\[ E(Y_{ki})=\mu_k \text{ and Var}(Y_{ki}) = \sigma_k^2 \text{ for } k=1,2 \text{ and } i= 1,2,\cdots,n_k \]

用樣本均值 \(\bar{Y}_k\) 作爲總體均值 \(\mu_k\) 的估計：

\[ \bar{Y}_k \sim N(\mu_k, \frac{\sigma_k^2}{n_k}) \text{ for } k=1,2 \]

如果兩個樣本的觀察值互相獨立，我們知道均值差 \(\bar{Y}_2 - \bar{Y}_1\)，也服從下面描述的正態分佈：

\[ \begin{equation} \bar{Y}_2-\bar{Y}_1 \sim N(\mu_2-\mu_1, \frac{\sigma^2_2}{n_2}+\frac{\sigma^2_1}{n_1}) \end{equation} \tag{25.1} \]

根據這個性質，可以計算均值差的統計量 \(Z\)：

\[ \begin{equation} Z=\frac{\bar{Y}_2-\bar{Y}_1}{\sqrt{(\sigma_2^2/n_2)+(\sigma_1^2)/n_1}} \sim N(\frac{\mu_2-\mu_1}{\sqrt{(\sigma_2^2/n_2)+(\sigma_1^2)/n_1}},1) \end{equation} \tag{25.2} \]

所以 \(\bar{Y}_2-\bar{Y}_1\) 的樣本分佈 (25.2)，就可以應用於爲 \(\mu_2-\mu_1\) 計算顯著性水平爲 \(\alpha\) 的 \(100(1-\alpha)\%\) 信賴區間，或者進行假設檢驗。

用信賴區間章節 (Section 22.4) 學到的方法，均值差的信賴區間的下限 \(L\)，和上限 \(U\)，分別是：

\[ \begin{aligned} L & = (\bar{Y}_2 - \bar{Y}_1) + z_{\alpha/2}\sqrt{\frac{\sigma_2^2}{n_2}+\frac{\sigma_1^2}{n_1}}\\ U & = (\bar{Y}_2 - \bar{Y}_1) + z_{1-\alpha/2}\sqrt{\frac{\sigma_2^2}{n_2}+\frac{\sigma_1^2}{n_1}} \end{aligned} \]

由於標準正態分佈左右對稱 \(z_{\alpha/2}=-z_{1-\alpha/2}\)，所以\(100(1-\alpha)\%\) 信賴區間爲：

\[ \begin{equation} (\bar{Y}_2 - \bar{Y}_1) \pm z_{1-\alpha/2}\sqrt{\frac{\sigma_2^2}{n_2}+\frac{\sigma_1^2}{n_1}} \end{equation} \tag{25.3} \]

進行均值差的假設檢驗時，零假設是均值差等於零 \(\text{H}_0: \mu_2-\mu_1 = 0\)；替代假設是均值差不等於零 \(\text{H}_1: \mu_2-\mu_1\neq0\)。

在零假設條件下 \(\mu_2-\mu_1 = 0\)，公式 (25.2) 計算的均值差的檢驗統計量 \(Z\) 服從標準正態分佈 \(Z\sim N(0,1)\)。根據章節 23.5 同理知雙側 \(p\) 值的計算式爲：

\[ \begin{equation} 2[1-\Phi(\frac{|\bar{y}_2-\bar{y}_1|}{\sqrt{(\sigma_2^2/n_2)+(\sigma_1^2/n_1)}})] \end{equation} \tag{25.4} \]

此時，我們進行的假設檢驗，計算的信賴區間用到的前提有：

兩組的觀察數據 \(Y_{ki}\) 均服從正態分佈；
所有的觀察對象互相獨立；
兩組數據來自的人羣的方差已知。

違反這些前提的話： 1. 如果不滿足前提 1，對統計結果影響不會很大，只要觀察樣本較大，均值或者均值差本身的樣本分佈也就服從了正態分佈 (中心極限定理)； 2. 如果不滿足前提 2，則不應該採用此方法，觀察對象本身如果有一定的結構構成或者不滿足相互獨立，本方法不適用； 3. 前提 3，大多數現實例子中都不太可能滿足，因爲總體/人羣的方差多數情況下都是未知的，所以，下一小節討論方差未知的情況，逐漸放寬我們的統計分析前提條件。

25.1.2 當方差未知，但是方差可以被認爲相等，且數據服從正態分佈 two sample \(t\) test

如果兩組數據來自的人羣可以被認爲方差是齊的 \(\sigma_1^2=\sigma_2^2=\sigma^2\)，公式 (25.1) 可以變爲：

\[ \bar{Y}_2-\bar{Y}_1 \sim N(\mu_2-\mu_1, \sigma^2(\frac{1}{n_2}+\frac{1}{n_1})) \]

但是這個分佈中的方差是未知的，所以除了均值和均值差，這個共同的方差也變成了需要用樣本方差 \(\hat{\sigma}^2\) 來作估計。此時，兩個樣本的方差的無偏估計爲，加權方差：

\[ \begin{equation} \hat\sigma^2 = \frac{(n_1-1)\hat\sigma^2_1+(n_2-1)\hat\sigma^2_2}{n_1+n_2-2} \end{equation} \tag{25.5} \]

因爲 \(\frac{(n_1-1)\hat\sigma^2_1}{\sigma^2} \sim \chi^2_{n_1-1}; \frac{(n_2-1)\hat\sigma^2_2}{\sigma^2} \sim \chi^2_{n_2-1}\)，所以兩樣本的加權方差 \(\hat\sigma^2\) 服從自由度爲 \(n_1+n_2-2\) 的卡方分佈：

\[ \frac{(n_1+n_2-2)\hat\sigma^2_1}{\sigma^2} \sim \chi^2_{n_1+n_2-2} \]

所以，此時的檢驗統計量 \(T\)，服從自由度爲 \(n_1+n_2-2\) 的 \(t\) 分佈：

\[ T=\frac{(\bar{Y}_2-\bar{Y}_1) - (\mu_2-\mu_1)}{\hat\sigma\sqrt{(1/n_2)+(1/n_1)}} \sim t_{n_1+n_2-2} \]

接下來就可以利用這個統計量進行假設檢驗，求均值差的 \(100(1-\alpha)\%\) 信賴區間，類比章節 22.5：

\[ (\bar{Y}_2-\bar{Y}_1) \pm t_{n_1+n_2-2, 1-\alpha/2}\hat\sigma\sqrt{(1/n_2)+(1/n_1)} \]

25.1.3 練習

下表展示的是，隨機將11名嬰兒分配到實驗組和對照組，記錄嬰兒能夠獨立行走的月齡。試用表格總結的數據進行能獨立行走的月齡的均值是否在實驗組和對照組之間有差異的假設檢驗，並求月齡均差的 \(95\%\) 信賴區間。

表 24.1: Children’s ages at time of first walking alone by randomisation group
	Age in months for walking alone
	Active exercise group (i=1)	Eight week control group (i=2)
	9.00, 9.50, 9.75, 10.00, 13.00, 9.50	13.25, 11.50, 12.00, 13.50, 11.50
\(n_i\)	6	5
\(\bar{Y}_i\)	10.125	12.350
\(\hat\sigma_i\)	1.447	0.962

解

假設 \(\text{H}_0: \mu_2-\mu_1 = 0 \text{ v.s } \text{H}_1: \mu_2-\mu_1 \neq 0\)

假如，實驗組對照組的月齡方差可以認爲是方差相同的，那麼他們的加權方差則可以計算爲：

\[ \hat\sigma^2 = \frac{(6-1)\times(1.447)^2+(5-1)\times(0.962)^2}{6+5-2} = \frac{14.172}{9} = 1.575 \]

零假設條件下，則檢驗統計量 \(T\) 服從自由度爲 \(9\) 的 \(t\) 分佈，本例的數據給出的檢驗統計量大小爲：

\[ T=\frac{12.350-10.125}{\sqrt{1.575\times(1/5+1/6)}} = \frac{2.225}{0.76} = 2.928 \]

通過查閱統計數據表格：

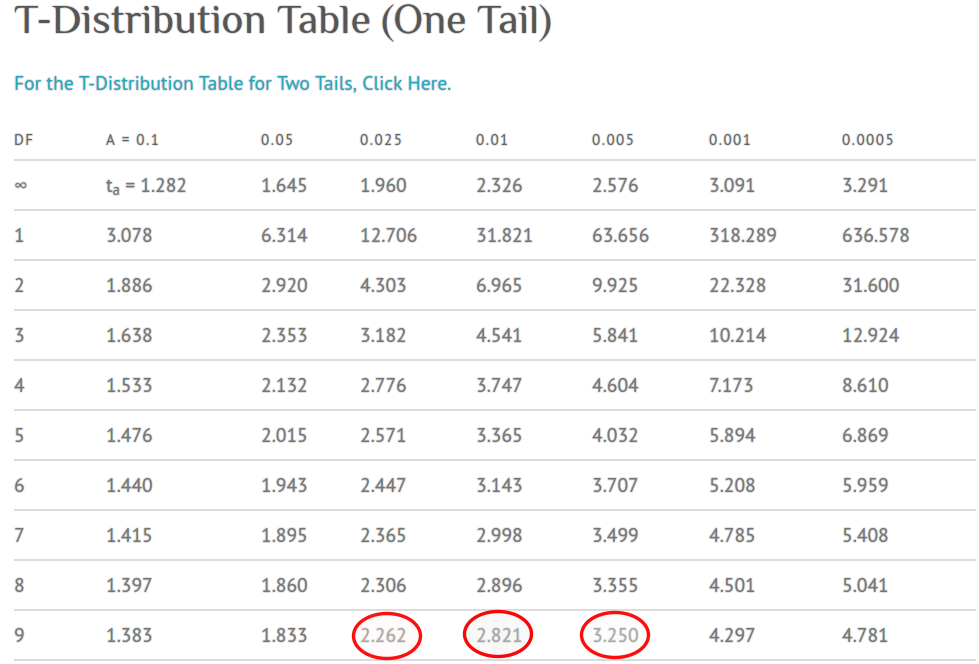
圖 25.1: T-Distribution table (0ne-Tail)

圖 25.1 中顯示統計量 \(t=2.928\) 的單側 \(p\) 值介於 \(0.01\sim0.005\) 之間，所以此例的雙側 \(0.01 < p < 0.02\)。

均值差 \(\mu_2-\mu_1\) 的 \(95\%\) 信賴區間爲：

\[ \begin{aligned} (\bar{Y}_2-\bar{Y}_1) &\pm t_{9, 0.975}\hat\sigma\sqrt{(1/n_2)+(1/n_1)} \\ = 2.225 &\pm 2.262 \times 0.76 = (0.51, 3.94) \end{aligned} \]

上面的手計算過程，如果你像我一樣運氣好可能在考場上碰到，實際生活中我們肯定是使用 R 進行計算拉。下面用了兩種不同的代碼，但是結果和目的都是一樣的： t.test() 時指定 var.equal = TRUE或者用簡單線性迴歸的代碼 lm()。

t.test(Walk$Age ~ Walk$Group, var.equal = TRUE)

## 
##  Two Sample t-test
## 
## data:  Walk$Age by Walk$Group
## t = -2.9, df = 9, p-value = 0.02
## alternative hypothesis: true difference in means between group exercise and group control is not equal to 0
## 95 percent confidence interval:
##  -3.9437 -0.5063
## sample estimates:
## mean in group exercise  mean in group control 
##                  10.12                  12.35

summary(lm(Age ~ Group, data = Walk))

## 
## Call:
## lm(formula = Age ~ Group, data = Walk)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -1.125 -0.738 -0.375  0.388  2.875 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    10.125      0.512   19.77    1e-08 ***
## Groupcontrol    2.225      0.760    2.93    0.017 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.25 on 9 degrees of freedom
## Multiple R-squared:  0.488,  Adjusted R-squared:  0.431 
## F-statistic: 8.58 on 1 and 9 DF,  p-value: 0.0168

25.1.4 當方差未知，但是方差不可以被認爲相等，且數據服從正態分佈

下一節會討論如何比較方差是否齊的手段，用於本節分析方法在實際應用時的參考。

當兩組連續型正態分佈的數據不能被認爲方差相同時，有幾種方法可以採用。一是將數據通過數學轉換 (log-transformed, etc.)，人爲的把方差的差異縮小以後，使用前一節的齊方差時的均值比較法 (two-sample \(t\) test)。另一種方法是，既然方差不齊，那就用各自的觀察數據來估計其方差 \((\hat\sigma_1^2, \hat\sigma_2^2)\)。只要各自的樣本量較大 \(n_1, n_2\)，兩組數據均值差 \(|\bar{y}_2-\bar{y}_1|\) 除以其合併後的標準誤 \(\sqrt{\frac{\hat\sigma_1^2}{n_1}+\frac{\hat\sigma_2^2}{n_2}}\)。利用公式 (25.3) 和 (25.4)，把已知的兩組數據各自的方差用樣本方差取代之後即可用於計算信賴區間，實施假設檢驗求 \(p\) 值。

但是，當兩組觀察數據的樣本量不大時 \((< 30)\)，根據 Welch–Satterthwaite 建議的，估計均值差除以估計標準誤服從一個自由度爲 \(n^*\) 的 \(t\) 分佈。值得注意的是，這個自由度並非正整數：

\[ n^*=\frac{(\frac{\hat\sigma_1^2}{n_1}+\frac{\hat\sigma_2^2}{n_2})^2}{[\frac{(\hat\sigma_1^2/n_1)^2}{n_1-1}] + [\frac{(\hat\sigma_2^2/n_2)^2}{n_2-1}]} \]

在 R 裏可以指定 var.equal = TRUE 進行 \(t\) 檢驗：

t.test(Walk$Age ~ Walk$Group, var.equal = FALSE)

## 
##  Welch Two Sample t-test
## 
## data:  Walk$Age by Walk$Group
## t = -3, df = 8.7, p-value = 0.01
## alternative hypothesis: true difference in means between group exercise and group control is not equal to 0
## 95 percent confidence interval:
##  -3.8879 -0.5621
## sample estimates:
## mean in group exercise  mean in group control 
##                  10.12                  12.35

值得注意的是在 R 裏面，\(t\) 檢驗是默認組間方差不齊的，如果你沒有指定 var.equal = TRUE，R 就會默認進行上面的方差不齊的 \(t\) 檢驗。

25.2 兩個人羣的方差比較

25.2.1 方差比值檢驗 variance ratio test

前一節介紹的樣本均值比較中一個重要的前提是方差齊不齊的問題，所以本節我們就來討論如何比較兩個人羣的方差是否相同，進而爲均值比較時是選用方差齊的檢驗方法 (two sample \(t\) test) 還是方差不齊的方法 (Welch Two Sample \(t\) test) 提供有價值的參考信息。

比較方差是否相同，最簡單的是利用 \(F\) 檢驗，也就是標題的方差比值檢驗 variance ratio test。和大多數檢驗方法一樣，多數情況下進行的也是雙側檢驗，零假設是方差齊，替代假設是方差不齊。

同前例，我們用 \(Y_{1i} (i=1,2,\cdots, n_1), Y_{2i} (i=1,2,\cdots,n_2)\) 標記兩組從兩個不同人羣中隨機觀察的獨立樣本數據。兩個數據服從正態分佈。檢驗統計量是兩個方差之比 \(F=\frac{\hat\sigma_1^2}{\hat\sigma_2^2}\)。這個比值距離零假設條件下的 1 越遠，證明兩個方差不相同的證據越強。

此時需要有 \(F\) 分佈的知識，具體的推導和證明需要參考統計推斷部分 (Section 17.2)，此處直接使用其結論。如果兩個獨立變量，各自服從相應自由度的卡方分佈，那麼他們各自除以自由度後的商，服從 \(F\) 分佈。正式的數學定義描述如下：

\[ \begin{aligned} & \text{If } A\sim \chi_a^2 \text{ and } B \sim \chi_b^2 \text{ independently} \\ & \text{then } F = \frac{A/a}{B/b} \sim F_{a,b} \end{aligned} \]

在應用方差比值檢驗時，零假設條件下 (方差相等)，兩方差自由度分別是 \(n_1-1, n_2-1\)，故 \(F=\frac{\hat\sigma_1^2}{\hat\sigma_2^2} \sim F_{n_1-1, n_2-1}\)，即服從自由度爲 \(n_1-1, n_2-1\) 的 \(F\) 分佈。所以需要比較計算所得的統計量 \(F\) 值的大小和相應自由度的 \(F\) 分佈。

比較方差大小時，習慣上先計算兩樣本的方差，然後把較大的那個當作分子除以較小的那個，由此計算的檢驗統計量就會總是大於 \(1\)。此時我們查閱統計表格獲得的 \(p\) 值是單側的，你可以將之乘以 \(2\)，或者計算另一半 \(p\) 值相加即可。\(F\) 檢驗高度依賴數據服從正態分佈這一前提。在 R 裏面 var.test() 是進行 \(F\) 檢驗的代碼，另外包 car 裏還有 leveneTest() 是一種更加穩健的比較方差的方法，適用於數據不服從正態分佈時：

var.test(Walk$Age~Walk$Group)

## 
##  F test to compare two variances
## 
## data:  Walk$Age by Walk$Group
## F = 2.3, num df = 5, denom df = 4, p-value = 0.4
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
##   0.2417 16.7226
## sample estimates:
## ratio of variances 
##              2.264

leveneTest(Age ~ Group, data = Walk, center = median)

## Levene's Test for Homogeneity of Variance (center = median)
##       Df F value Pr(>F)
## group  1       0   0.95
##        9

25.2.2 信賴區間

類比章節 22.6，可以容易地推導出方差比值 \(\frac{\sigma_1^2}{\sigma_2^2}\) 的 \(95\%\) 信賴區間公式爲：

\[ \begin{equation} (\frac{F}{F_{n_1-1,n_2-1, 0.975}} , \frac{F}{F_{n_1-1,n_2-1,0.025}}) \end{equation} \tag{25.6} \]

上面的式子會需要計算檢驗統計量 \(F\) 值左側的 \(p\) 值，一般的檢驗統計表個不提供。但是利用 \(F\) 分佈的性質如果 \(F\sim F_{a,b}\) 那麼 \(\frac{1}{F} \sim F_{b,a}\) ，所以下面的公式在查閱表格時更加實用：

\[ (\frac{F}{F_{n_1-1,n_2-1, 0.975}} , F\times F_{n_2-1,n_1-1,0.975}) \]

25.3 比較兩個百分比

25.3.1 兩個百分比差是否爲零的推斷 Risk difference

令 \(R_1, R_2\) 爲兩種不同實驗的成功次數，每種實驗進行的次數分別是 \(n_1, n_2\)。類似地，令 \(P_1, P_2\) 表示兩種實驗的觀察勝率。所以 \(R_1, R_2\) 服從二項分佈：\(R_k \sim \text{Bin}(n_k, \pi_k) \text{ for } k=1,2\)。所以有：

\[ \begin{aligned} & E(P_k) = \pi_k \text{ and Var}(P_k) = \frac{\pi_k(1-\pi_k)}{n_k} \\ & \text{For } k = 1,2 \text{ and } P_1, P_2 \text{ independent } \end{aligned} \]

當 \(n_k\) 足夠大，每個百分比都可以根據中心極限定理用下面的正態分佈來近似：

\[ P_k \sim N(\pi_k, \frac{\pi_k(1-\pi_k)}{n_k}) \text{ for } k= 1,2 \]

由於兩樣本是獨立的，所以百分比差也是服從下面的正態分佈的：

\[ \begin{equation} P_2-P_1 \sim N(\pi_2-\pi_1, \frac{\pi_1(1-\pi_1)}{n_1}+\frac{\pi_2(1-\pi_2)}{n_2}) \end{equation} \tag{25.7} \]

所以，作大樣本的百分比比較時，百分比差 \(\pi_2-\pi_1\) 的 \(100(1-\alpha)\%\) 信賴區間公式爲：

\[ (P_2-P_1) \pm z_{1-\alpha/2}\sqrt{\frac{P_1(1-P_1)}{n_1}+\frac{P_2(1-P_2)}{n_2}} \]

進行的百分比差的假設檢驗爲： \(\text{H}_0: \pi_2-\pi_1 = 0 \text{ v.s. H}_1: \pi_2-\pi_1 \neq 0\) 檢驗統計量 \(Z\) 爲：

\[ \begin{aligned} & Z=\frac{P_2-P_1}{\sqrt{P(1-P)(\frac{1}{n_2}+\frac{1}{n_1})}} \sim N(0,1) \\ & \text{Where } P=\frac{R_1+R_2}{n_1+n_2} \text{ is the marginal probability of success} \\ & p\text{-value} = 2\times(1-\Phi\{ \frac{|P_2-P_1|}{\sqrt{P(1-P)(\frac{1}{n_2}+\frac{1}{n_1})}} \}) \end{aligned} \]

25.3.2 兩個百分比商是否爲 1 的推斷 relative risk/risk ratio

兩個百分比商，在流行病學中通常使用相對危險度 (relative risk) 或者危險度比 (risk ratio) 來表示。從樣本數據中獲得的相對危險度比的估計爲 \(RR=\frac{P_2}{P_1}\)。樣本量大時，百分比近似服從正態分佈，所以百分比差也近似服從正態分佈，然而百分比商則不然。此時用到數據的轉換，將百分比商求對數以後 \(\text{log}\frac{P_2}{P_1}\) ，得到近似正態分佈的對數樣本分佈進而進行假設檢驗，計算信賴區間。

下一章會着重介紹數據的轉換 (transformation)，本章暫且先用其結論，當 \(Y_k=\text{log}(P_k)\) ，其方差爲 \(\text{Var}(Y_k) = \frac{1-\pi_k}{n_k\pi_k}\)，所以此方差的估計量爲 \(\frac{1-P_k}{R_k}\)。

由此可得 \(\text{log}\frac{\pi_2}{\pi_1}\) 的 \(95\%\) 信賴區間公式爲：

\[ \text{log} \frac{P_2}{P_1} \pm 1.96\times\sqrt{\frac{1-P_1}{R_1}+\frac{1-P_2}{R_2}} \]

如果把上面式子計算的 \(\text{log}\frac{\pi_2}{\pi_1}\) 的 \(95\%\) 信賴區間標記爲 \((L,U)\)，那麼相對危險度 \(\frac{\pi_2}{\pi_1}\) 的 \(95\%\) 信賴區間爲 \((exp(L), exp(U))\)。

第 25 章 比較 Comparisons