第 16 章 假設檢驗的近似方法
本章教你怎麼徒手搞似然比檢驗 (likelihood ratio test),Wald 檢驗 (Wald test),和 Score 檢驗 (Score test)。
16.1 近似和精確檢驗 approximate and exact tests
前一章描述了如何用對數似然比尋找最佳檢驗統計量 (Section 15.3)。一旦找到並確定了最佳檢驗統計量,接下去還需要確定這個最佳檢驗統計量的樣本分佈,用定好的顯著性水平(\(\alpha=0.05\))確定拒絕域,再使用觀察數據計算數據本身的統計量,然後對反對零假設的證據定量(計算 \(p\) 值) 。前一章用的例子均來自於正態分佈,所以我們都能夠不太複雜地獲得樣本均值,樣本方差等較容易取得樣本分佈的檢驗統計量。正如我們在前一章最後部分 (Section 15.7) 總結的那樣,大多數情況下我們沒有那麼幸運。最佳檢驗統計量的樣本分佈會很難確定。所以另一個進行假設檢驗的途徑就是近似檢驗法 (approximate tests)。
16.2 精確檢驗法之 – 似然比檢驗法 Likelihood ratio test
記得我們之前說到,簡單假設 \(H_0: \theta=\theta_0\text{ v.s. } H_1: \theta=\theta_1\) 的檢驗的最佳檢驗統計量可以使用 Neyman-Pearson lemma (尼曼皮爾森輔助定理) (Section 15.3) 來確定:
\[\ell_{H_0}-\ell_{H_1} = \ell(\theta_0)-\ell(\theta_1)\]
如果假設變成了複合型假設:\(H_0: \theta\in\omega_0 \text{ v.s. } H_1: \theta\in\omega_1\)。此時,\(\omega_0, \omega_1\) 分別指兩種假設條件下我們關心的總體參數的可能取值範圍。那麼可以把上面的定理擴展成,在 \(\omega_0, \omega_1\) 兩個取值範圍內,零假設和對立假設在給出的觀察數據條件下的極大似然之比:
\[\text{log}\frac{\text{max}_{H_0}[L(\theta|data)]}{\text{max}_{H_1}[L(\theta|data)]}=\text{max}_{H_0}[\ell(\theta|data)]-\text{max}_{H_1}[\ell(\theta|data)]\\ =\text{max}_{\theta\in\omega_0}[\ell(\theta|data)]-\text{max}_{\theta\in\omega_1}[\ell(\theta|data)]\]
典型的假設檢驗情況下,我們面對的是簡單的零假設和複合型的替代假設:
\[H_0: \theta=\theta_0 \text{ v.s. } H_1: \theta\neq\theta_0\]
所以在這個情況下,套用擴展以後的 Neyman-Pearson lemma:
\[\text{max}_{H_0}[\ell(\theta)]-\text{max}_{H_1}[\ell(\theta)]=\ell(\theta_0) - \ell(\hat\theta)=llr(\theta_0)\]
之前討論對數似然比 (Section 13.3) 時我們已知:
\[\text{Under }H_0: \theta=\theta_0\Rightarrow -2llr(\theta_0)\stackrel{\cdot}{\sim}\mathcal{X}_1^2\]
於是利用自由度爲 \(1\) 的卡方檢驗的特徵我們就可以爲反對零假設的證據定量,計算關鍵的拒絕域。如果說顯著性水平爲 \(\alpha\) 那麼,我們拒絕零假設 \(H_0:\theta=\theta_0\) 的拒絕域是:
\[-2llr(\theta_0)>\mathcal{X}^2_{1,1-\alpha}\]
當使用 \(\alpha=0.05\) 時,這個關鍵的拒絕域就是:\(-2llr(\theta_0)>3.84\)。
這就是傳說中的 (對數) 似然比檢驗,(log-)Likelihood ratio test (LRT)。
LRT 的優點:
- 簡單;
- \(p\) 值不會被參數尺度 (parameter scale) 左右,也就是說如果我們對參數進行了數學轉換 (Section 14.2) 也不會影響似然比檢驗計算得到的 \(p\) 值大小。
LRT 的缺點:
- 非正態分佈的數據時,LRT 只能算是漸進有效 (asymptotic valid),即樣本量要足夠大時結果才能令人滿意;
- 無法總是保證這是最佳檢驗統計量;
- 需要計算兩次對數似然 (MLE 和 零假設時)。
16.3 練習題
假設有在觀察對象 \(n=100\) 人中發生了 \(k=40\) 個事件。假定數據服從二項分佈,已知人羣中每個人發生該事件的概率爲 \(\pi_0=0.5\)。嘗試計算似然比檢驗統計量:\(-2llr(\pi_0)\),並進行顯著性水平爲 \(\alpha=0.05\) 的假設檢驗:\(H_0: \pi=\pi_0 \text{ v.s. }H_1: \pi\neq\pi_0\)
解
\[ \begin{aligned} &\because f(k=40|\pi) = \binom{100}{40}\pi^{40}(1-\pi)^{100-40} \\ &\text{Ignoring terms} \text{ not with } \pi \\ &\therefore \ell(\pi|k=40) = 40\text{log}\pi+60\text{log}(1-\pi) \\ &\Rightarrow \ell^\prime(\pi|k=40) = \frac{40}{\pi}-\frac{60}{1-\pi} \\ &\text{Let } \ell^\prime(\pi|k=40) = 0 \\ &\Rightarrow \frac{40}{\pi}-\frac{60}{1-\pi} =0 \\ &\Rightarrow \text{ MLE } \hat\pi=0.4 \\ &\Rightarrow llr(\pi_0)=\ell(\pi_0)-\ell(\hat\pi) \\ &\;\;\;\;\;\;\;\;\;=40\text{log}0.5+60\text{log}(1-0.5)-40\text{log}0.4-60\text{log}(1-0.4)\\ &\;\;\;\;\;\;\;\;\;=-2.013\\ &\Rightarrow -2llr=4.026 > \text{Pr}(\mathcal{X}^2_{1,0.95})=3.84 \end{aligned} \]
所以當顯著性水平爲 \(\alpha=0.05\) 時,數據提供了足夠拒絕零假設的證據。該事件在此人羣中發生的概率要低於人羣的 \(0.5\)。
16.4 近似檢驗法之 – Wald 檢驗
和 LRT 一樣, Wald 檢驗也適用於檢驗 \(H_0: \theta=\theta_0 \text{ v.s. } H_1: \theta\neq\theta_0\)。但是本方法其實是使用對數似然比方程的近似二次方程 (Section 14)。相比之下,LRT 使用的是精確的對數似然比,只對檢驗統計量 \(-2llr\) 進行了自由度爲 \(1\) 的卡方分佈 \(\mathcal{X}_1^2\) 近似。本節介紹的 Wald 檢驗過程中使用了兩次近似,一次是計算對數似然比時使用了二次方程,一次則是和 LRT 一樣對檢驗統計量進行 \(\mathcal{X}_1^2\) 近似。
根據之前的對數似然比近似結論 (Section 14.1) :
\[llr(\theta)\approx-\frac{1}{2}(\frac{M-\theta}{S})^2\text{ asymptotically}\]
其中,\(M\) 是 \(\text{MLE }\hat\theta\),\(S=\sqrt{\left.-\frac{1}{\ell^{\prime\prime}(\theta)}\right\vert_{\theta=\hat{\theta}}}\)
而且前一節我們也看到,
\[ \text{Under }H_0: \theta=\theta_0\Rightarrow -2llr(\theta_0) \stackrel{\cdot}{\sim}\mathcal{X}_1^2\\ \Rightarrow -2\times-\frac{1}{2}(\frac{M-\theta_0}{S})^2 \stackrel{\cdot}{\sim}\mathcal{X}_1^2 \\ \Rightarrow (\frac{M-\theta_0}{S}) \stackrel{\cdot}{\sim} N(0,1)\\ \text{Let } W=(\frac{M-\theta_0}{S}) \]
\(W\) 就是我們在 Wald 檢驗中用到的檢驗統計量。接下來就可以計算給定顯著水平 \(\alpha\) 時的拒絕域,給 \(p\) 值定量:
當 \(W>N(0,1)_{1-\alpha/2}\) 或 \(W<N(0,1)_{\alpha/2}\)時,拒絕 \(H_0: \theta=\theta_0\);
或者,當 \(W^2>\mathcal{X}^2_{1,1-\alpha}\) 時,拒絕 \(H_0: \theta=\theta_0\)。
這就是我們心心念念的 Wald 檢驗。
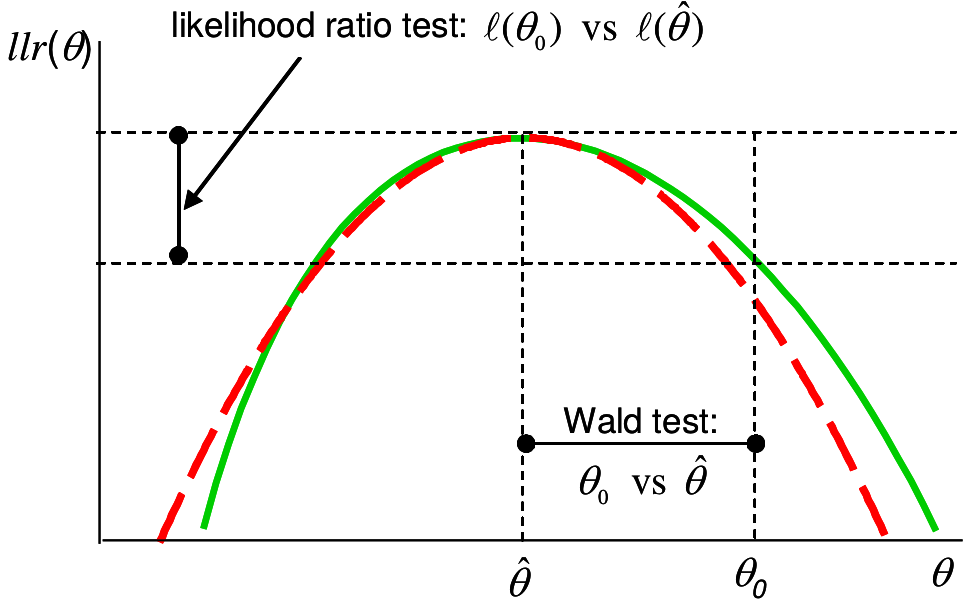
圖 16.1: Likelihood ratio and Wald tests: solid (green) line is log-likelihood ratio, dashed (red) is quadratic approximation
上圖 16.1 解釋了 LRT 和 Wald 檢驗的不同之處。紅色虛線是二次方程,用於近似似然比方程(綠色實線) 。二者在 \(\text{MLE}=\hat\theta\) 時同時取極大值。Wald 檢驗的是,數據提供的 \(\hat\theta\) 和我們想要比較的零假設 \(\theta_0\) 之間的橫軸差距。在檢驗量 \(W\) 中我們還把這個差除以觀察數據均值的標準差(數據的標準誤) 。 如果數據本身波動大,\(W\) 的分母(標準誤) 較大,那麼即使 \(\hat\theta - \theta_0\) 保持不變,統計量變小,反對零假設的證據也就越小。反觀,LRT 檢驗的檢驗統計量就是上圖 16.1 顯示的縱軸差 \(\ell(\theta_0)-\ell(\hat\theta)\) 的大小。二者之間的關係被直觀的顯示在圖中。
Wald 檢驗優點:
- 比 LRT 略簡單;
- 不必再計算零假設時的對數似然,只需要 \(MLE\) 和它的標準誤。
Wald 檢驗缺點:
- 兩次近似(LRT只用了一次近似) ;
- 無法總是保證這是最佳檢驗統計量;
- 參數如果被數學轉換 (Section 14.2),\(p\) 值會跟着變化。
16.4.1 再以二項分佈爲例
在 \(n\) 個實驗對象中觀察到 \(k\) 個事件,使用參數爲 \(\pi\) 的二項分佈模型來模擬。使用 Wald 檢驗法對下列假設做出統計檢驗: \(H_0: \pi=\pi_0 \text{ v.s. } H1: \pi\neq\pi_0\)。將參數 logit 轉換 (log-odds) 之後,對轉換後的新參數再做一次 Wald 檢驗。
解
根據之前的二次方程近似法推導 (Section 14.1.3):
\[ \begin{aligned} & M=\text{MLE}=\hat\pi=\frac{k}{n}=p\\ & S=se(\hat\pi)=\sqrt{\frac{p(1-p)}{n}}\\ & \Rightarrow \text{Under } H_0: \pi=\pi_0\\ & W=(\frac{p-\pi_0}{\sqrt{\frac{p(1-p)}{n}}})\stackrel{\cdot}{\sim} N(0,1) \end{aligned} \]
根據參數數學轉換的性質 (Section 14.2)
\[ \begin{aligned} &\text{New parameter } \beta=g(\pi)=\text{logit}(\pi)=\text{log}\frac{\pi}{1-\pi}\\ & \text{MLE}=\text{logit}(\hat\pi)=\text{log}\frac{\hat\pi}{1-\hat\pi} \\ & \text{Here we need to use delta-method to approximate standard error of } g(\pi)\\ & S=se[g(\hat\pi)]\approx g^\prime(\pi)\times se(\hat\pi) \\ & = \frac{1}{\hat\pi(1-\hat\pi)}\sqrt{\frac{p(1-p)}{n}}\\ & =\sqrt{\frac{1}{k}+\frac{1}{n-k}} \\ & \text{So the Wald test becomes}\\ & H_0: \beta=\beta_0\\ & \Rightarrow W=\frac{\text{log}(\frac{\hat\pi}{1-\hat\pi})-\text{log}(\frac{\pi_0}{1-\pi_0})}{\sqrt{\frac{1}{k}+\frac{1}{n-k}}}\stackrel{\cdot}{\sim} N(0,1) \end{aligned} \]
可見對參數進行了數學轉換之後,檢驗統計量的計算式發生了變化。因此 \(p\) 值也會不同。
16.5 近似檢驗法之 – Score 检验
注意到 Wald 檢驗使用的近似二次方程是在 MLE, 也就是極大似然比時的點 \(\hat\theta\) 和對數似然比方程取相同的值和相同曲率 (二次導數)。 可以類比的是,Score 检验是基于另一種二次方程模擬,Score 檢驗的近似二次方程和對數似然比方程在零假設 (\(\theta_0\)) 時取相同的曲率。所以,Score 檢驗使用的近似方程在 \(\theta_0\) 時和對數似然比方程在相同位置時的傾斜度 (一階導數),和曲率 (坡度的變化程度,二階導數) 相同。所以令 \(U\) 爲對數似然比方程在 \(\theta_0\) 時的坡度,定義 \(V\) 是對數似然比方程在 \(\theta_0\) 時的曲率的負數:
\[ \begin{aligned} & U=\ell^\prime(\theta)|_{\theta=\theta_0}=\ell^\prime(\theta_0)\\ & V=-E[\ell^{\prime\prime}(\theta)]|_{\theta=\theta_0}=-E[\ell^{\prime\prime}(\theta_0)] \end{aligned} \]
注:此處的 \(V=-E[l^{\prime\prime}(\theta_0)]\) 又常常被叫做 Expected Fisher information。
記得在 Wald 檢驗中使用的近似方程: \[llr(\theta)\approx-\frac{1}{2}(\frac{M-\theta}{S})^2\text{ asymptotically}\]
令 \(q(\theta)=-\frac{1}{2}(\frac{M-\theta}{S})^2\) 就有:
\[ \begin{aligned} & q^\prime(\theta) =\frac{M-\theta}{S^2}\\ & \Rightarrow q^\prime(\theta_0) =\frac{M-\theta_0}{S^2}\\ & q^{\prime\prime}(\theta) =-\frac{1}{S^2}\\ & \Rightarrow q^{\prime\prime}(\theta_0)=E[l^{\prime\prime}(\theta_0)]\\ & \Rightarrow \frac{1}{S^2} =-E[l^{\prime\prime}(\theta_0)]\\ & q^\prime(\theta_0) = \frac{M-\theta_0}{S^2} = -E[l^{\prime\prime}(\theta_0)](M-\theta_0)\\ & = \ell^\prime(\theta_0)\\ & \Rightarrow M-\theta_0 = -\frac{\ell^\prime(\theta_0)}{E[l^{\prime\prime}(\theta_0)]}\\ & \Rightarrow M = -\frac{\ell^\prime(\theta_0)}{E[l^{\prime\prime}(\theta_0)]}+\theta_0\\ & q(\theta)=-\frac{1}{2}(\frac{M-\theta}{S})^2=\frac{E[l^{\prime\prime}(\theta_0)]}{2}(-\frac{\ell^\prime(\theta_0)}{E[l^{\prime\prime}(\theta_0)]}+\theta_0-\theta)^2\\ & q(\theta)=-\frac{V}{2}(\frac{U}{V}+\theta_0-\theta)^2\\ & \Rightarrow \text{ Under } H_0: \theta=\theta_0\\ & \Rightarrow q(\theta_0)=-\frac{V}{2}(\frac{U}{V})^2=-\frac{U^2}{2V}\\ & \Rightarrow -2q(\theta_0)=\frac{U^2}{V} \stackrel{\cdot}{\sim}\mathcal{X}_1^2\\ & \text{Or equivalently} \frac{U}{\sqrt{V}} \stackrel{\cdot}{\sim} N(0,1) \end{aligned} \]
這就是 Score 檢驗時使用的檢驗統計量。相應的拒絕域就可以被定義爲: 當 \(\frac{U^2}{V}>\mathcal{X}_{1,1-\alpha}^2\) 時,拒絕 \(H_0\)
如下面的示意圖 16.2 所示,Score 檢驗,比較的是 \(\theta_0\) 時的校正後似然方程的坡度 (一階導數/二階導數),和極大似然時的坡度 (一階導數=0) 的差別。如果這個值越大,說明零假設時的似然和極大似然 (觀察數據的信息) 的距離越遠,拒絕零假設的證據就越有力。
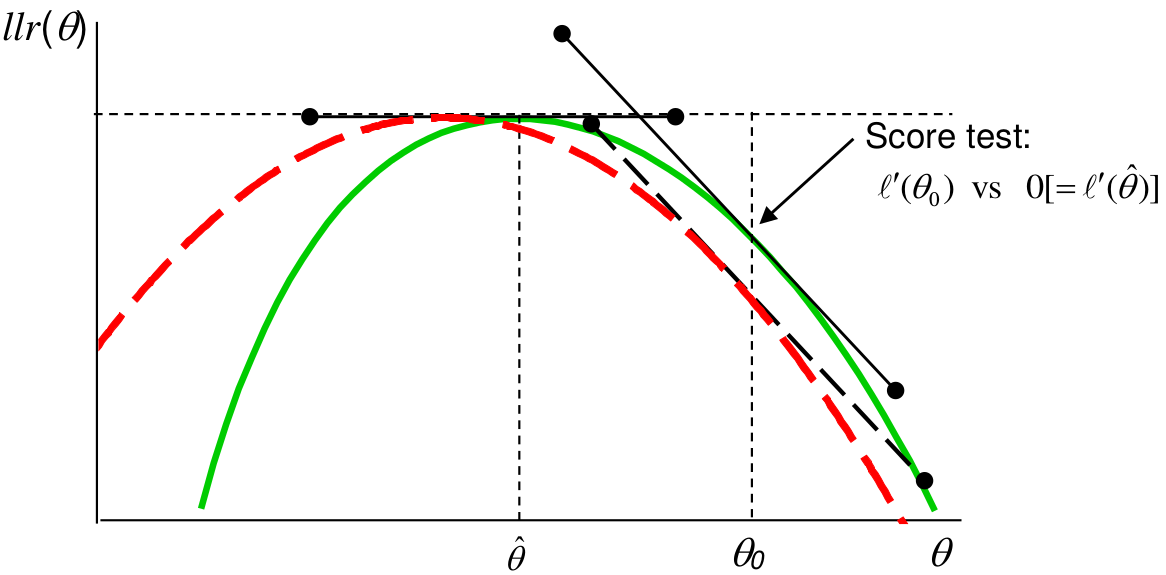
圖 16.2: Score test: solid (green) line is log-likelihood ratio, dashed (red) is quadratic approximation
Score 檢驗優點:
- 比 LRT 簡單;
- 不需要計算 MLE,只需要計算零假設時的對數似然比方程之坡度和曲率;
- 在流行病學用到的檢驗方法中最常用,也最容易擴展 (Mantel-Haenszel test, log rank test, generalised linear models such as logistic, Poisson, Cox regressions)。
Score 檢驗缺點:
- 和 Wald 檢驗一樣用到了兩次近似;
- 無法總是保證這是最佳檢驗統計量;
- 參數如果被數學轉換 (Section 14.2),\(p\) 值會跟着變化。
16.5.1 再再以二項分佈爲例
\(K\sim Bin(n, \pi)\) 假如已知人羣中事件發生的概率是 \(\pi_0\)。試推導此時的 Score 檢驗的檢驗統計量。
解
對二項分佈數據進行 Score 檢驗的時候我們需要計算 \(U, V\),然後計算統計量 \(\frac{U^2}{V}\) 和 \(\mathcal{X}_1^2\) 比較即可。
\[ \begin{aligned} & \text{Let } p=\frac{k}{n} \\ & \ell(\pi|k) = k\text{log}(\pi)+(n-k)\text{log}(1-\pi)\\ & \ell^\prime(\pi)=\frac{k}{\pi}-\frac{n-k}{1-\pi}=\frac{k-n\pi}{\pi(1-\pi)}\\ & = \frac{p-\pi}{\pi(1-\pi)/n}\\ & \Rightarrow U = \ell^\prime(\pi_0)=\frac{p-\pi_0}{\pi_0(1-\pi_0)/n}\\ & \ell^{\prime\prime}(\pi|K)=-\frac{K}{\pi^2}-\frac{n-K}{(1-\pi)^2}\\ & \Rightarrow -\ell^{\prime\prime}(\pi|K)=\frac{K}{\pi^2}+\frac{n-K}{(1-\pi)^2}\\ & \because E(K)=n\pi\\ & \therefore -E[\ell^{\prime\prime}(\pi|K)]=\frac{n\pi}{\pi^2}+\frac{n-n\pi}{(1-\pi)^2}\\ & =\frac{n}{\pi}+\frac{n}{1-\pi}=\frac{n}{\pi(1-\pi)}\\ & \text{ Under } H_0: \pi=\pi_0 \Rightarrow V=-E[\ell^{\prime\prime}(\pi_0)]=\frac{n}{\pi_0(1-\pi_0)}\\ & \Rightarrow \frac{U^2}{V}=\frac{(p-\pi_0)^2}{\pi_0(1-\pi_0)/n} \stackrel{\cdot}{\sim}\mathcal{X}_1^2\\ & \text{OR } \frac{U}{\sqrt{V}} = \frac{p-\pi_0}{\sqrt{\pi_0(1-\pi_0)/n}} \stackrel{\cdot}{\sim} N(0,1) \end{aligned} \]
16.6 LRT, Wald, Score 檢驗三者的比較
LRT 比較的是對數似然方程在零假設 \(H_0\) 和極大似然估計 (MLE) 時之間的縱軸差 (圖 16.1);Wald 檢驗試圖直接比較 MLE 和 \(H_0\) 的橫軸差 (二次方程近似法,並用標準誤校正) (圖 16.1);Score 檢驗比較的是對數似然方程在 \(H_0\) 時的切線斜率 (二次方程近似法,用曲率也就是二階導數校正) (圖 16.2)。三種檢驗比較的東西各不相同,但是這種差距大到進入拒絕域時,數據就會拒絕零假設。其中 Score 檢驗的計算過程最爲簡便,只需要計算 \(H_0\) 時對數似然方程的一階和二階導數,而不用去計算 MLE,因此更多的被應用在流行病學數據計算中。
如果對數似然方程本身就是左右對稱的 (正態分佈的情況下),這三個檢驗方法計算的所有結果都是完全一致的。如果對數似然方程只是近似左右對稱,那麼三者的計算結果會十分接近。可以說,三種檢驗方法是漸進等價的。
如果對觀測值進行了數學轉換,三者中只有 LRT 的計算結果保持不變。如果對參數的數學轉換使得對數似然方程更加接近左右對稱的二次方程,那麼 Wald 和 Score 檢驗的計算結果可以得到改善。
如果說,MLE 和 零假設之間的差距很大,那麼 Wald 或者 Score 檢驗所使用的二次方程近似法的誤差會增加,此時傾向於使用 LRT 來進行精確檢驗。當然如果當樣本量較大,要檢驗的差距也很大,三種檢驗方案都能夠提供證據拒絕零假設 (\(p\) 值都會很小)。
如果三種檢驗方案給出的計算結果迥異,即使使用了數學轉換結果也沒有明顯改善的話,那麼最大的問題是樣本量太小。這時候還是老老實實用 LRT 吧。
幾乎所有的參數檢驗都歸類與這章節介紹的三種檢驗方法。比如說 \(Z\) 檢驗, \(t\) 檢驗, \(F\) 檢驗都是 LRT。在流行病學研究中最常用的還是 Score 檢驗。
我們的結論是,當條件允許的情況下,統計檢驗都推薦儘量使用精確檢驗 LRT。
16.7 Inference Practical 08
16.7.1 Q1
在對數似然比章節 (Section 13.2),我們曾經證明過,已知方差時:
\[ \begin{aligned} & llr(\mu|\underline{x})=\ell(\mu|\underline{x})=-\frac{1}{2}(\frac{\bar{x}-\mu}{\sigma/\sqrt{n}})^2\\ & \Rightarrow -2llr(\mu|\underline{x})=-2\ell(\mu|\underline{x})=(\frac{\bar{x}-\mu}{\sigma/\sqrt{n}})^2 \end{aligned} \]
當觀察數據 \(X_1,\cdots,X_n\sim N(\mu,1^2)\) ,求 LRT, Wald, Score 三種檢驗方法對下列假設進行檢驗時的檢驗統計量: \(H_0: \mu=\mu_0 \text{ v.s. } H_1: \mu\neq\mu_0\)
解
\[ \begin{aligned} & \text{Model: } X_1, \cdots, X_n \stackrel{i.i.d}{\sim} N(\mu, 1)\\ & H_0: \mu=\mu_0 \text{ v.s. } H_1: \mu\neq\mu_0\\ & \text{Model } \Rightarrow \bar{X} \sim N(\mu, \frac{1}{n}) \\ & \text{If we observe } \bar{X} = \bar{x}\\ & \ell(\mu|\bar{x})=-\frac{1}{2}(\frac{\bar{x}-\mu}{1/\sqrt{n}})^2\\ & \textbf{For LRT, under } H_0: \mu=\mu_0 \Rightarrow -2llr(\mu_0) \stackrel{\cdot}{\sim}\mathcal{X}_1^2\\ & \Rightarrow \frac{\bar{x}-\mu}{1/\sqrt{n}} \sim N(0,1)\\ & \textbf{For Wald test, under } H_0: \mu=\mu_0 \Rightarrow \frac{M-\mu_0}{S}\sim N(0,1) \\ & \Rightarrow \frac{\bar{x}-\mu}{1/\sqrt{n}} \sim N(0,1)\\ & \textbf{For Score test, under } H_0: \mu=\mu_0 \Rightarrow U=\ell^\prime(\mu_0), V=-E[\ell^{\prime\prime}(\mu_0)]\\ & U=\ell^\prime(\mu_0)=(\frac{\bar{x}-\mu_0}{1/\sqrt{n}})\sqrt{n}=\frac{\bar{x}-\mu_0}{1/n}\\ & \ell^{\prime\prime}(\mu_0)=-\frac{1}{1/n}=-n \Rightarrow V=-E[n]=n\\ & \frac{U^2}{V}=(\frac{\bar{x}-\mu_0}{1/n})^2/n=(\frac{\bar{x}-\mu_0}{1/\sqrt{n}})^2\\ & \Rightarrow \frac{U^2}{V} \sim \mathcal{X}_1^2 \Rightarrow \frac{U}{\sqrt{V}}=\frac{\bar{x}-\mu_0}{1/\sqrt{n}} \sim N(0,1) \end{aligned} \]
本題證明了,當數據服從正態分佈時,三種檢驗方法使用的檢驗統計量,是完全一致的。
16.7.2 Q2
根據醫生的觀察,某種癌症患者的生存時間服從平均值爲 \(1/\beta_0\) 的指數分佈 (exponentially distributed)。有一種新藥物可以改善平均生存時間 (仍然服從指數分佈)。已知指數分佈的密度方程是:\(f(x|\beta)=\beta \text{exp} (-\beta x), \text{ where } \beta, x>0\)。
- 證明指數分佈的均值是 \(1/\beta\)
解
\[ \begin{aligned} & X\sim f(x|\beta), x>0 \Rightarrow E(X)=\int_0^\infty x\cdot f(x)\text{d} x = \int_0^\infty x\cdot \beta \cdot e^{-\beta x} \text{d}x\\ & E(x)= - \int_0^\infty x\cdot \frac{\text{d}e^{-\beta x}}{\text{d}x} \cdot \text{d}x\\ & \text{We can now integrate by parts, using } \int_a^b u \frac{\text{d}v}{\text{d}x} \text{d}x = [uv]_a^b-\int_a^b v \frac{\text{d}u}{\text{d}x} \text{d}x \\ & E(X) = -[x\cdot e^{-\beta x}]_0^\infty + \int_0^\infty e^{-\beta x} \text{d} x \\ & \;\;\;\; = -0+\int_0^\infty e^{-\beta x} \text{d} x\\ & \;\;\;\; = \int_0^\infty\frac{\text{d}}{\text{d}x} \frac{e^{-\beta x}}{-\beta} \text{d} x\\ & \;\;\;\; = [\frac{e^{-\beta x}}{-\beta}]_0^\infty = \frac{1}{-\beta}[0-1]=\frac{1}{\beta} \end{aligned} \]
- 請寫下本題設定條件下的數學模型,零假設和替代假設
解: 假設患者人數爲 \(n\),他們的生存時間爲相互獨立的隨機變量: \(X_1,\cdots,X_n\)。那麼本例中的數學模型爲:\(\text{Model: } X_1,\cdots,X_n\stackrel{i.i.d}{\sim}f(x|\beta)=\beta e^{-\beta x}\)。我們可以提出如下的零假設和替代假設:\(H_0: \beta=\beta_0 \text{ v.s. } H_1: \beta\neq\beta_0\)。
- 推導此模型參數 \(\beta\) 的極大似然估計 (MLE),試使用似然比檢驗法來推導進行假設檢驗時使用的檢驗統計量。
解
\[ \begin{aligned} & L(\beta|\underline{x}) = \prod_{i=1}^n f(x_i|\beta)=\prod_{i=1}^n\beta e^{-\beta x_i} \\ & \ell(\beta)=\sum_{i=1}^n\text{log}(\beta e^{-\beta x_i})=\sum\text{log}\beta-\sum\beta x_i=n\text{log}\beta-\beta\sum x_i \\ & \;\;\;\; = n\text{log}\beta-\beta n \bar{x} \\ & \Rightarrow \ell^\prime(\beta)=\frac{n}{\beta}-n\bar{x}\text{ MLE solves } \ell^\prime(\beta)=0 \text{ when }\ell^{\prime\prime}(\beta) < 0 \\ & \ell^\prime(\beta)=0 \Rightarrow \hat\beta=\frac{1}{\bar{x}}, \text{ and } \ell^{\prime\prime}(\beta)=-n\frac{1}{\beta^2} < 0\\ & \Rightarrow \text{ LRT test statistic: Under } H_0: \beta=\beta_0 \Rightarrow -2llr(\beta_0) \sim \mathcal{X}_1^2\\ & llr(\beta_0)=\ell(\beta_0)-\ell(\hat\beta)=n\text{log}\beta_0-\beta_0n\bar{x}-n\text{log}\hat\beta+\hat\beta n \bar{x}\\ & \text{ Substituting with MLE } \hat\beta=\frac{1}{\bar{x}}\\ & \;\;\;\;\;\;\;\;\;\; = n\text{log}\beta_0-\beta_0n\bar{x}+n\text{log}\bar{x}+ n\\ & \;\;\;\;\;\;\;\;\;\; = n(\text{log}\beta_0\bar{x}-\beta_0\bar{x}+1) \textbf{ this is the statistic for LRT} \end{aligned} \]
- 推導 Score 和 Wald 檢驗法時的檢驗統計量
解
\[ \begin{aligned} & \textbf{Score test: under } H_0 \Rightarrow \frac{U^2}{V}\sim \mathcal{X}_1^2 \text{ where } U=\ell^\prime(\beta_0), V=-E[\ell^{\prime\prime}(\beta_0)]\\ & \Rightarrow U=\frac{n}{\beta_0}-n\bar{x}; V = -E[-n\frac{1}{\beta_0^2}] = n\frac{1}{\beta_0^2} \\ & \Rightarrow \frac{U^2}{V}=(\frac{n}{\beta_0}-n\bar{x})^2\cdot\frac{\beta_0^2}{n} = (\frac{(\frac{n}{\beta_0}-n\bar{x})\beta_0}{\sqrt{n}})^2\\ & \;\;\;\;\;\;\;\;\; = n(1-\bar{x}\beta_0)^2\\ & \textbf{This is the statistic for Score test}\\ & \textbf{Wald test: under } H_0: \beta=\beta_0 \Rightarrow W=(\frac{M-\beta_0}{S})^2 \sim \mathcal{X}_1^2, \\ & \text{ where } M=\hat\beta=\frac{1}{\bar{x}}, \text{ and } S^2=-\frac{1}{\ell^{\prime\prime}(\hat\beta)}\\ & \ell^{\prime\prime}(\beta)=-n\frac{1}{\beta^2}\Rightarrow \ell^{\prime\prime}(\hat\beta)=-n\bar{x}^2\Rightarrow S^2=\frac{1}{n\bar{x}^2}\\ & \Rightarrow W=(\frac{M-\beta_0}{S})^2=\frac{(\frac{1}{\bar{x}}-\beta_0)^2}{\frac{1}{n\bar{x}^2}}=n(1-\beta_0\bar{x})^2\\ & \textbf{This is the statistic for Wald test} \end{aligned} \]
注意到在這個特例中, Score 和 Wald 檢驗的統計量竟然不謀而合。
- 觀察5名患者,獲得診斷後的生存數據 (年): \(0.5,1,1.25,1.5,0.75\)。用上面推導的統計量對這個數據進行假設檢驗:\(H_0: \beta=0.5 \text{ v.s. } \beta\neq0.5\),你如何下結論?
解
\[ \begin{aligned} &\text{Data: } x_1,\cdots,x_n=0.5,1,1.25,1.5,0.75. \Rightarrow \bar{x}=1\\ &H_0: \beta=0.5 \text{ v.s. } \beta\neq0.5\\ &\textbf{LRT test: } \\ & llr(\beta_0) = n(\text{log}\beta_0\bar{x}-\beta_0\bar{x}+1) = 5\times(\text{log}0.5-0.5\times1+1) = -0.966\\ &\Rightarrow -2llr=1.93 < \text{Prob}(\mathcal{X}^2_{1,0.95}) = 3.84 \\ & \text{There is no evidence that } \beta\neq0.5.\\ &\textbf{Score test: } \\ & \frac{U^2}{V} = n(1-\bar{x}\beta_0)^2 = 5\times(1-1\times0.5)^2=1.25 < \text{Prob}(\mathcal{X}^2_{1,0.95}) = 3.84 \\ & \text{There is no evidence that } \beta\neq0.5.\\ &\textbf{Wald test: } \\ & W=n(1-\beta_0\bar{x})^2=5\times(1-0.5\times1)^2=1.25< \text{Prob}(\mathcal{X}^2_{1,0.95}) = 3.84 \\ & \text{There is no evidence that } \beta\neq0.5.\\ \end{aligned} \]