第 85 章 生存分析入門
- The best thing about being a statistician is that you get to play in everyone’s backyard.
- John Tukey
85.1 本章概要
本章內容包括以下幾個部分
- 怎樣描述生存數據,刪失值的定義
- 如何定義風險度方程,生存方程,概率密度方程
- 描述生存數據各個方程之間的數學關係
- 定義指數分佈,Weibull 分佈,對數邏輯分佈,並懂得這些分佈適合哪些類型的生存數據
- 準確寫出這三個分佈下的生存數據的似然
- 使用R分析生存數據的初步設定
- 理解並解釋在R中分析獲得的生存模型的參數
85.2 什麼是生存分析 What is survival analysis?
生存分析,研究的是隨訪中研究對象發生我們關心的事件與否,以及比較發生該事件之前時間的長短 (生存時間) 的一種分析方法。生存數據的常見例子如下:
- 死亡 (all cause);
- 診斷/治療後直至死亡發生的時間;
- 孕婦的懷孕時間 (孕期長短);
- 對象以健康狀態進入研究時開始,直至其診斷爲患有某種疾病的時間。
生存分析中的常見術語:
- 生存時間 survival time = 失敗時間 failure time = 事件時間 event time。
- 生存分析本身常被叫做事件史分析 time-to-event analysis。
生存分析的結果,可以用來回答很多我們關心的問題:
- 研究特定人羣中,在某段時間內人口生存 (或死亡) 的模式 (平均壽命): 在英國,某年 (例如 1970 年) 出生的人,能夠生存到 5 歲,40 歲,100 歲的概率是多大? (關心的是死亡在某人身上發生的概率)
- 比較兩組或多組人羣之間,不同的特徵導致的死亡時間的差異大小的估計: 某種新療法對於同時被診斷爲相同程度肺癌的患者,和標準療法相比是否能有效延長其生存時間?
- 研究多種變量 (例如體重,年齡,性別,吸煙,飲食等) 和事件發生時間長短之間的關系: 例如收集健康對象,研究其體質指數 (BMI) 和最終發生二型糖尿病幾率之間的關系,同時要調整其他已知的混雜因素。
- 預測特定患者的存活幾率: 肝癌患者診斷後的 5 年生存率,10 年生存率的推算。
85.3 生存數據在哪裏
生存數據其實很常見,下面是幾個例子:
- 特定國家特定時間內對人口出生死亡的登記數據;
- 在隨機雙盲對照臨牀試驗中,治療組和安慰劑組相比,治療組的生存時間是否真的較長;
- 前瞻性隊列研究;
- 非醫學的例子也有很多,例如分析暴風雪降臨之前的時間,或者推測地震可能發生的幾率。
85.4 生存數據分析之前要理清楚的問題
- 對於結果/事件的定義;
- 研究的時間起點;
- 研究的時間單位是用的月份,周,還是年,是觀察時間,還是患者的實際年齡 (實際年齡就是實際生存時間);
- 事件發生時的時間,是否被精確定義了?
85.5 生存數據的左右截尾
沒有哪個研究能保證觀察隨訪到所有的研究對象最終是否發生了事件 (死亡),有些對象在研究中途就會退出實驗。所以這些沒有觀察到事件發生,但是在研究的過程中貢獻了生存時間數據的對象,被稱爲刪失數據 (censored)。刪失數據又根據其發生原因的不同被分爲下面幾種:
- 行政刪失 (administrative censoring): 如果最終事件,被定義爲死亡的話,研究者不大可能等到所有的觀察對象都死亡 (可能耗時幾十年) 之後再分析數據,而是認爲地定義某個時間點作爲研究結束,不再隨訪的時間。
- 隨訪失敗 (loss to follow-up): 無論是幹預型實驗,還是觀察性實驗,有些觀察對象中途無法聯系上,或者改變主義推出實驗的人並不少見。這些對象的出現都意味着研究者無法再對他們進行事件發生與否的觀察了。
- 死於其他原因 (death from other causes): 可能某些研究只關心患者吸煙習慣與死於肺癌的時間長短的關系,當某些觀察對象確實發生了死亡事件,但是死因並不是肺癌時 (肝癌,或者自殺,車禍等),這些人也被認爲是刪失數據。
上述幾種可能發生的刪失數據,這幾種類型的刪失數據,被叫做右側刪失數據 (right censoring),在分析中不能被刪除,因爲他們在未離開研究之前,我們確定他們是沒有發生事件的,他們的觀察時間也應當被放入統計模型中加以考慮。
85.6 初步分析生存數據
生存數據,比較的是生存時間。由於時間本身是連續型變量,我們可能會想到利用處理連續型變量時的方法來進行初步的比較:
- 每個人生存時間的柱狀圖 (histogram);
- 計算生存時間的簡單統計量: 中位數 (median)。
即使是拿穩健統計學方法比較治療組和對照組的中位數是否不同,也無法解決刪失數據的問題。我們需要新的方法來處理生存數據。
85.7 初步描述生存數據
描述生存數據的統計學正式方案是:
- 生存方程 the survival function
- 風險度方程和累積風險度 the hazard function and the cumulative hazard
- 概率密度方程 the probability density function
85.7.1 生存方程
生存方程的定義是,觀測生存時間 \(T\),大於某個時間 \(t\) 的概率:
\[ S(t) = \text{Pr}(T > t) \]
累計概率方程是
\[ F(t) = \text{Pr}(T \leqslant t) = 1 - S(t) \]
85.7.2 風險度方程
風險度有時候就只叫做風險 (hazard),時間 \(t\) 時的風險度爲 \(h(t)\)。風險度方程被定義爲:
\[ h(t) = \lim_{\delta\rightarrow0}\frac{1}{\delta}\text{Pr}(t\leqslant T < t + \delta | T\geqslant t) \]
風險度利用的是數學中的極限理論,表示在時間 \(t\) 和時間 \(t+\delta\) (其中\(\delta \rightarrow 0\)) 之間,觀察對象沒有發生事件的概率。風險度的概念明白了以後,風險度在時間軸上的積分,就被叫做累積風險度:
\[ H(t) = \int_0^th(u)\text{d}u \]
85.7.3 概率密度方程
和其他的方程類似,常用 \(f(t)\) 標記生存時間的概率密度方程:
\[ f(t) = \frac{\text{d}}{\text{d}t}F(t) = \lim_{\delta\rightarrow0}\frac{1}{\delta}\text{Pr}(t\leqslant T < t + \delta) \]
85.7.4 各方程之間的關系
\[ \begin{aligned} f(t) & = \frac{\text{d}}{\text{d}t}F(t) = \frac{\text{d}}{\text{d}t}\{ 1-S(t) \} = - \frac{\text{d}}{\text{d}t}S(t) \\ S(t) & = 1 - F(t) = 1 - \int_0^t f(u)\text{d}u = \int_t^\infty f(u)\text{d}u \\ h(t) & = \lim_{\delta\rightarrow0}\frac{1}{\delta}\text{Pr}(t \leqslant T < t+ \delta | T > t) \\ & = \lim_{\delta\rightarrow0}\frac{1}{\delta}\frac{\text{Pr}(t \leqslant T < t+ \delta, T > t)}{\text{Pr}(T > t)} (\text{Bayes' Theroem}) \\ & = \lim_{\delta\rightarrow0}\frac{1}{\delta}\frac{\text{Pr}(t \leqslant T < t+ \delta)}{\text{Pr}(T > t)} \\ & = \frac{f(t)}{S(t)} \\ h(t) & = \frac{f(t)}{S(t)} = \frac{\frac{\text{d}}{\text{d}t}F(t)}{S(t)} = \frac{- \frac{\text{d}}{\text{d}t}S(t)}{S(t)} = - \frac{\text{d}}{\text{d}t}\text{log}[S(t)] \\ \end{aligned} \]
推導 \(S(t), H(t)\) 之間的關系:
\[ \begin{aligned} \because h(t) & = - \frac{\text{d}}{\text{d}t}\text{log}[S(t)] \\ \text{intergrate both} & \text{ sides over the range from 0 to }t: \\ \int_0^th(u)\text{d}u & = - \int_0^t\frac{\text{d}}{\text{d}u}\text{log}[S(t)]\text{d}u \\ & = -[\text{log } S(u)]_{u = 0}^{u = t} \\ & = -[\text{log } S(t) - \text{log } S(0)] \\ & = -\text{log }S(t) \\ \Rightarrow S(t) & = \exp\{ - \int_0^th(u)\text{d}u\} = \exp\{ -H(t) \} \end{aligned} \]
85.8 生存時間的參數分布
85.8.1 指數分布
適用於生存時間最簡單的分布是指數分布 (exponentiential distribution)。指數分布默認風險率 (hazard rate,\(\lambda\)) 不隨時間變化。在指數分布中,風險度方程,生存方程和概率密度方程分別是:
\[ \begin{aligned} h(t) & = \lambda, \\ S(t) & = e^{-\lambda t} \\ f(t) & = h(t)S(t) \\ & = \lambda e^{-\lambda t} \end{aligned} \tag{85.1} \]
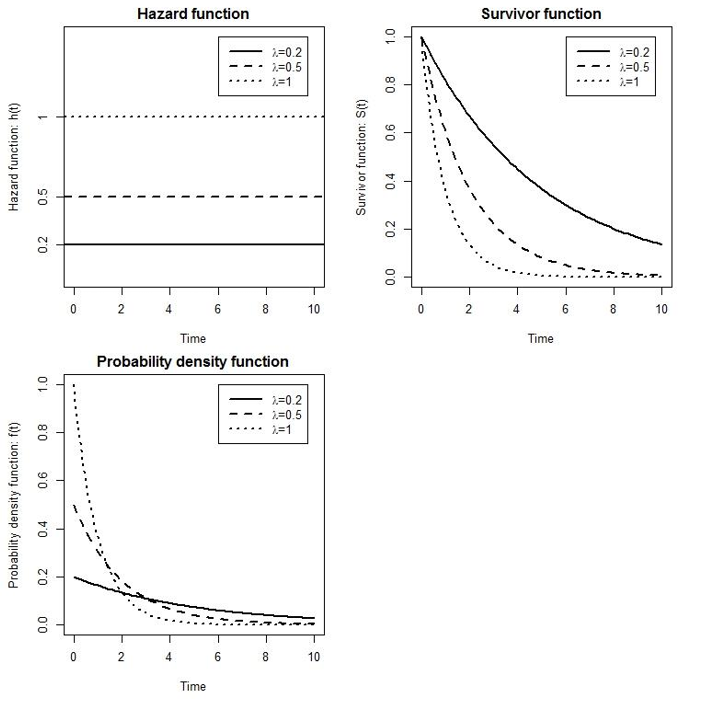
圖 85.1: The hazard function, survivor function and probability density function under an exponential distribution for survival times
85.8.2 Weibull 分布
指數分布的前提 – 事件發生率相同的假設過於強硬,許多真實數據,都不能滿足這個前提條件。另一個比指數分布靈活的分布是 Weibull 分布。它包含兩個參數,其風險度方程,生存方程和概率密度方程分別是:
\[ \begin{aligned} h(t) & = \kappa\lambda t^{\kappa - 1} \\ S(t) & = \exp(-\lambda t^\kappa) \\ f(t) & = \kappa \lambda t^{\kappa - 1} \exp(-\lambda t^\kappa) \end{aligned} \tag{85.2} \]
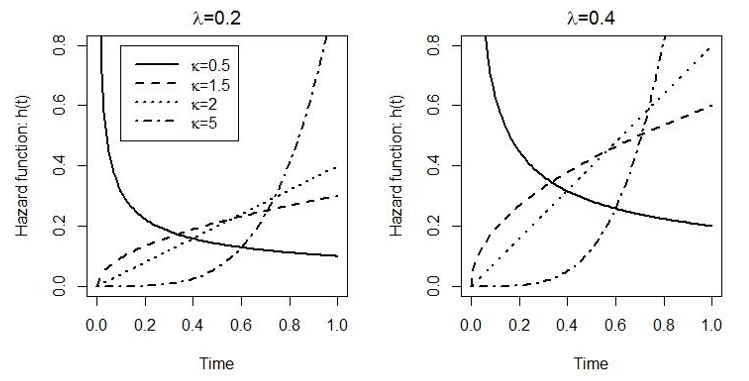
圖 85.2: Illustrations of the hazard function under a Weibull distribution with different shape (kappa) and scale (lambda).
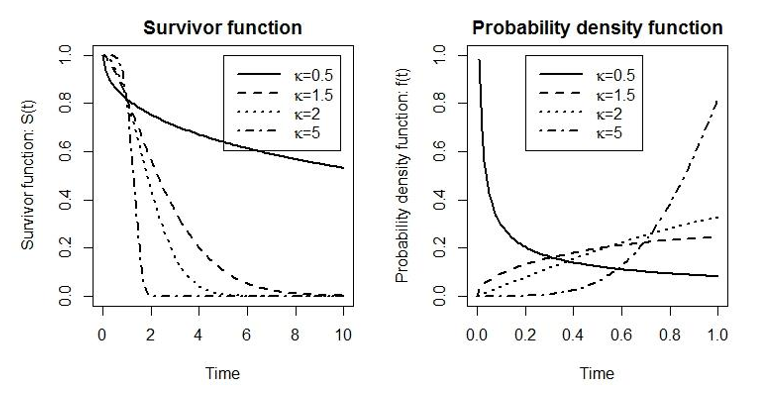
圖 85.3: Illustrations of the survival function and probability function under a Weibull distribution with different shape (kappa) and scale parameter lambda = 0.2.
當 \(\kappa = 1\) 時,Weibull 分布就降級爲簡單指數分布。從圖中也可以看出,Weibull 分布只允許風險度隨着時間單調遞增/遞減。
除了這兩個常見的生存時間分布,另外還有許多不同類型的分布。練習題中也會再探索 log-logistic 分布的應用。
85.9 極大似然法估計
假設,我們決定使用上面描述的簡單分布 - 指數分布來做爲生存時間的分布。接下來,就可以利用學習過的統計推斷的知識,對其做極大似然估計。
假設 \(n\) 名研究對象編號各自爲 \(i = 1, \cdots,n\),研究者對他們完成了從起點時間 (time origin) 起的隨訪。有些人發生了相關事件 (Event),所以,他們的生存時間 \(t_{E_i}\)。有些人則由於各種原因變成了刪失值,他們的生存時間是 \(t_{C_i}\)。關於刪失對象我們確切知道在時間 \(t_{C_i}\) 之內,他們沒有發生相關事件,且他們退出研究之後是否發生了事件不得而知。我們再根據觀察對象是否發生相關事件,在模型中生成一個啞變量 \(\delta_i\),當 \(\delta_i = 1\) 時,該對象的觀察生存時間是 \(t_{E_i}\),當 \(\delta_i = 0\) 時,該對象的觀察生存時間就是 \(t_{C_i}\):
\[ \delta_{i}=\left\{ \begin{array}{ll} 1 \text{ if } t_{E_i} \text{ observed} \\ 0 \text{ if } t_{C_i} \text{ observed}\\ \end{array} \right. t_{i}=\left\{ \begin{array}{ll} t_{E_i} \text{ if } \delta_i = 1 \\ t_{C_i} \text{ if } \delta_i = 0 \\ \end{array} \right. \]
| Individual | Survival or censoring time | Indicator of outcome or censoring |
|---|---|---|
| \(1\) | \(t_1\) | \(\delta_1\) |
| \(2\) | \(t_2\) | \(\delta_2\) |
| \(3\) | \(t_3\) | \(\delta_3\) |
| . | . | . |
| . | . | . |
| . | . | . |
| \(n\) | \(t_n\) | \(\delta_n\) |
對於那些觀察到事件的人,他們各自對似然的貢獻是 \(f(t_{E_i})\); 對於那些成爲刪失值的人,他們各自對似然的貢獻是 \(S(t_{C_i})\),所以該數據的似然就是:
\[ \begin{aligned} L & = \prod_{\text{Events}}f(t_{E_i})\prod_{\text{Censorings}}S(t_{C_i}) \\ & = \prod_i f(t_i)^{\delta_i} S(t_i)^{1-\delta_i} \\ & = \prod_i \{ h(t_i)S(t_i) \}^{\delta_i}S(t_i)^{1-\delta_i} \text{ because } h(t) = \frac{f(t)}{S(t)} \\ & = \prod_i h(t_i)^{\delta_i} S(t_i) \end{aligned} \]
極大似然法對各個參數的估計就可以用我們在統計推斷中使用的求對數極大似然的方法:
\[ \begin{aligned} \ell & = \sum_i[\delta_i\text{log}f(t_i) + (1-\delta_i)\text{log}S(t_i)] \\ & = \sum_i\{\delta_i\text{log}(\lambda e^{-\lambda t_i}) + (1-\delta_i)\text{log}(e^{-\lambda t_i}) \} \\ & = \sum_i\{ \delta_i\text{log}\lambda - \delta_i\lambda t_i -\lambda t_i + \delta_i\lambda t_i \} \\ & = \sum_i[\delta_i \text{log}\lambda - \lambda t_i] \\ & = \sum_i\delta_i\text{log}\lambda - \lambda\sum_it_i \\ \Rightarrow \ell^\prime & = \frac{\sum_i\delta_i}{\lambda} - \sum_i t_i \\ \text{let } \ell^\prime & =0 \Rightarrow \hat\lambda = \frac{\sum_i\delta_i}{\sum_i t_i}\\ \text{Because }\ell^{\prime\prime} & = -\frac{\sum_i\delta_i}{\lambda^2} < 0 \\ \text{Therefore } \hat\lambda & = \frac{\sum_i\delta_i}{\sum_it_i} \\ \text{ is the MLE for} & \text{ survival time follows exponential distribution.} \end{aligned} \]
85.10 Practical Survival 01
85.10.1 生存分析的時間尺度
85.10.1.1 把 PBC 數據讀入 R 中,d, time, datein, dateout 是什麼含義?
pbcbase <- read_dta("../backupfiles/pbcbase.dta")
# d 是表示是否發生事件的變量
# d = 0 表示該觀察對象是刪失值
# d = 1 表示該觀察對象在研究隨訪中死亡
# datein 是該觀察對象進入臨牀試驗的日期
# dateout 是該觀察對象發生死亡事件/變成刪失值的日期
# time 是從進入臨牀試驗到發生死亡時間或者變成刪失值這段時間的長度,以年爲單位
head(pbcbase[,1:5])## # A tibble: 6 × 5
## id datein dateout time d
## <dbl> <date> <date> <dbl> <dbl>
## 1 5 1980-02-19 1981-09-19 1.58 1
## 2 22 1980-08-22 1980-08-22 0 0
## 3 23 1980-07-22 1989-08-02 9.03 0
## 4 40 1980-08-08 1982-11-21 2.29 1
## 5 42 1980-09-06 1982-10-05 2.08 1
## 6 45 1980-02-09 1985-06-02 5.31 185.10.1.2 你認爲該研究應該使用哪種時間尺度?
這是一個比較兩種治療方案哪個更能延長患者生命時間的臨牀實驗,正確的時間尺度應該是從進入試驗開始,直至發生事件 (死亡) 或者離開試驗的這段時間 (隨訪時間 follow-up time)。
85.10.1.3 試驗中,多少患者發生了死亡事件,又有多少患者是刪失值?
## d :
## Frequency Percent Cum. percent
## 0 95 49.7 49.7
## 1 96 50.3 100.0
## Total 191 100.0 100.0# 第一例死亡發生在隨訪開始的 0.025 年,最後一例死亡發生在隨訪開始的 9.26 年;
# 所有對象中隨訪時間最長達到 11.64 年。
# 死亡事件發生的病例中,隨訪時間的中位數是 2.85 年
# 刪失對象的病例中,隨訪時間的中位數是 4.62 年。
with(pbcbase, epiDisplay::summ(time[d==1], graph = FALSE))## obs. mean median s.d. min. max.
## 96 3.243 2.847 2.357 0.025 9.259## obs. mean median s.d. min. max.
## 95 4.587 4.616 3.052 0 11.64485.10.1.4 讀入另一個數據 whitehall.dta,使用是否發生冠心病 chd 變量作爲事件變量。仔細觀察其時間的格式,timein, timeout, timebth,各自是什麼含義?1987 年 1 月 30 日發生了什麼事件?
whitehall <- read_dta("../backupfiles/whitehall.dta")
# timebth 是每個患者的出生日期
# timein 是每個患者進入試驗的日期,且注意到許多患者的進入試驗日期是相同的
# timeout 是隨訪結束的日期,對於 chd = 1 的人,這個日期是其死於冠心病的日期,
# 其餘的人則是刪失日期,且注意到許多刪失日期都是1987年1月30日,推測這是行政刪失日期。
whitehall[,c(1,3,12:14)]## # A tibble: 1,677 × 5
## id chd timein timeout timebth
## <dbl> <dbl> <date> <date> <date>
## 1 5001 0 1967-09-13 1987-01-30 1920-03-20
## 2 5019 0 1967-09-13 1987-01-30 1911-08-06
## 3 5038 0 1967-09-13 1987-01-30 1916-04-03
## 4 5039 0 1967-09-13 1987-01-30 1916-08-02
## 5 5042 0 1967-09-13 1983-04-12 1912-03-20
## 6 5052 0 1967-09-13 1984-07-10 1913-04-07
## 7 5064 0 1967-09-15 1984-05-13 1921-04-30
## 8 5078 1 1967-09-15 1983-11-29 1919-12-25
## 9 5089 0 1967-09-15 1987-01-30 1919-10-11
## 10 5090 0 1967-09-15 1987-01-30 1908-03-31
## # … with 1,667 more rows85.10.1.5 應該使用哪種時間尺度作爲此研究的時間呢?
很顯然,本實驗可以使用隨訪時間,作爲時間尺度。當然,考慮到不同的人進入實驗時的年齡不同,也可以用隨訪年齡作爲時間尺度。需要注意的是,如果使用年齡作爲時間尺度,不能使用 timeout - timebth 也就是隨訪結束減去出生日期作爲時間變量。因爲這樣的做法默認了所有人從出生時,就進入了實驗,這是無論如何也無法做到的。所以我們要用下面的第二個計算時間的代碼 M1,來考慮進入實驗時的年齡。因爲,進入實驗時,該觀察對象沒有發生事件,這已經是一個生存偏倚,需要告訴軟件加以考慮。注意比較三種方法計算的時間的最小值最大值的差別。
# 用隨訪時間做時間尺度
M0 <- survfit(Surv(time = (timeout - timein)/365.25, event = chd)~1, data = whitehall)
epiDisplay::summ(M0$time, graph = FALSE)## obs. mean median s.d. min. max.
## 702 13.96 16.678 5.307 0.151 19.381# 考慮了左側截尾的時間尺度
M1 <- survfit(Surv(agein, agein + (timeout - timein)/365.25, event = chd) ~ 1, data = whitehall)
epiDisplay::summ(M1$time, graph = FALSE)## obs. mean median s.d. min. max.
## 1670 68.568 67.888 6.582 44.391 85.766# 錯誤地認爲所有人都從出生日期開始進入試驗的時間尺度
M2 <- survfit(Surv((timeout - timebth)/365.25, event = chd) ~ 1, data = whitehall)
epiDisplay::summ(M2$time, graph = FALSE)## obs. mean median s.d. min. max.
## 1563 68.638 67.986 6.651 44.391 85.76685.10.2 擬合最簡單的指數分布生存數據
## # A tibble: 100 × 1
## surv.times
## <dbl>
## 1 0.442
## 2 2.01
## 3 2.26
## 4 1.64
## 5 9.88
## 6 1.19
## 7 3.72
## 8 7.14
## 9 11.3
## 10 6.69
## # … with 90 more rowsexp.model <- survreg(Surv(surv.times) ~ 1, dist = "exponential", data = mydata)
# 值得注意的是,在 R 裏擬合指數分布的生存數據時,計算獲得的是 -log(lambda)
summary(exp.model)##
## Call:
## survreg(formula = Surv(surv.times) ~ 1, data = mydata, dist = "exponential")
## Value Std. Error z p
## (Intercept) 1.527 0.100 15.27 <2e-16
##
## Scale fixed at 1
##
## Exponential distribution
## Loglik(model)= -252.7 Loglik(intercept only)= -252.7
## Number of Newton-Raphson Iterations: 5
## n= 100## (Intercept)
## 0.21727013## (Intercept)
## 0.1785987## (Intercept)
## 0.2643149585.10.3 探索服從 Weibull 分布時風險度方程的曲線
wei.haz <- function(x, lambda, kappa) {
kappa*lambda*x^(kappa - 1)
}
curve(wei.haz(x, 0.2, 0.5), ylim = c(0,0.8), xlab = "Time", ylab = "Hazard function")
curve(wei.haz(x, 0.2, 1.5), add = TRUE, col = "blue")
curve(wei.haz(x, 0.2, 1), add = TRUE, lty = 2)
curve(wei.haz(x, 0.2, 2), add = TRUE, col = "red")
curve(wei.haz(x, 0.2, 5), add = TRUE, col = "green")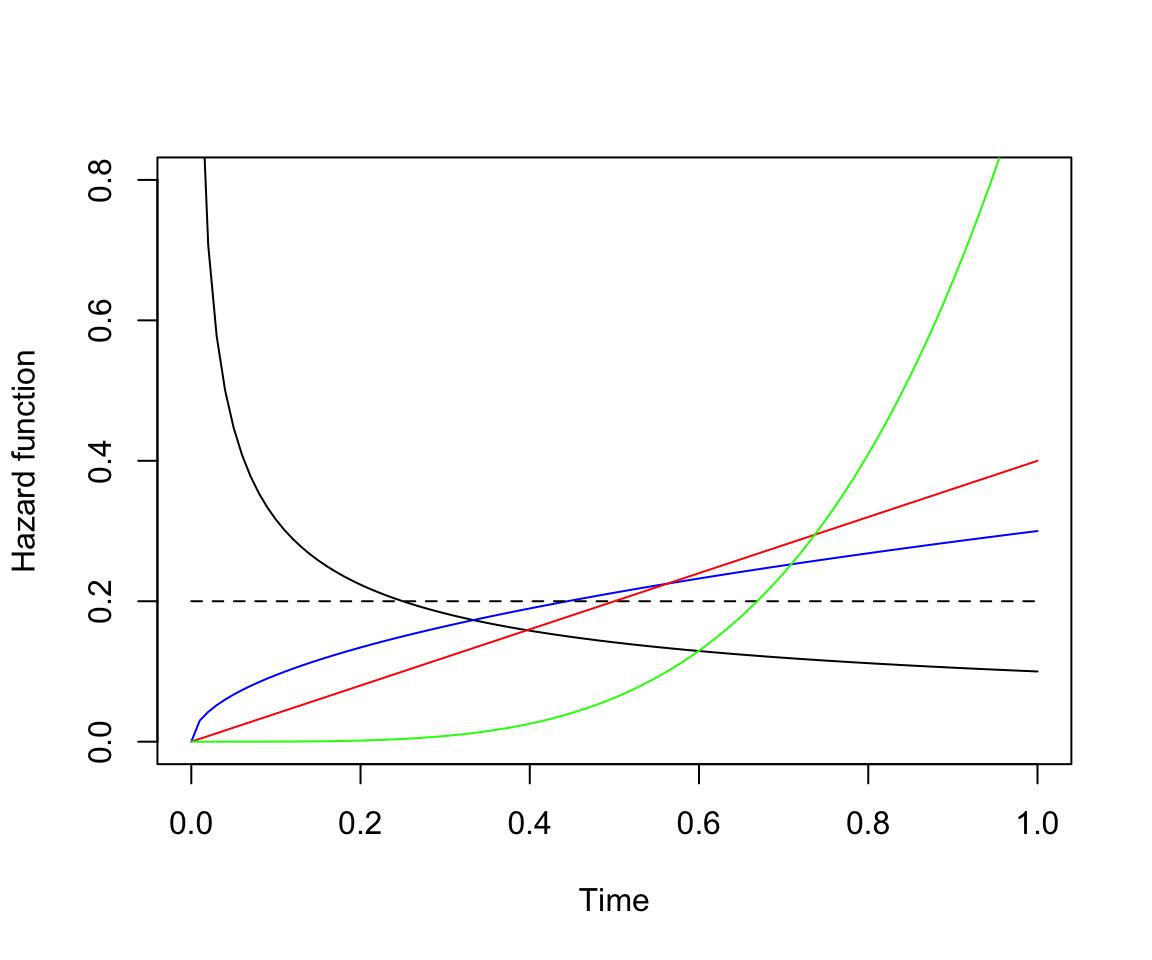
圖 85.4: Illustrations of the hazard function under a Weibull distribution with lambda = 0.2, and different shape (kappa)
在 Weibull 分布下,參數 \(\kappa\) 決定了風險度曲線的形狀。 \(\kappa < 1\) 時,風險度隨着時間下降,\(\kappa > 1\) 時,風險度隨着時間上升。當 \(\kappa = 1\) 時,Weibull 分布降級爲簡單的指數分布 (圖中點狀直線)。當 \(\kappa = 2\) 時,風險度和時間成線性關系。
85.10.4 探索 對數邏輯 (log-logistic) 分布時,風險度方程曲線會有哪些特性?
\[ h(t) = \frac{e^\theta \kappa t^{\kappa -1}}{1 + e^\theta t^\kappa} \]
loglog.haz <- function(x, theta, kappa) {
exp(theta)*kappa*x^(kappa - 1)/(1 + exp(theta)*x^kappa)
}
curve(loglog.haz(x, 1, 0.2), ylim=c(0,6), xlab = "Time", ylab = "Hazard function", col = "red")
curve(loglog.haz(x, 1, 2), add = T, col = "black")
curve(loglog.haz(x, 3, 2), add = T, col = "blue")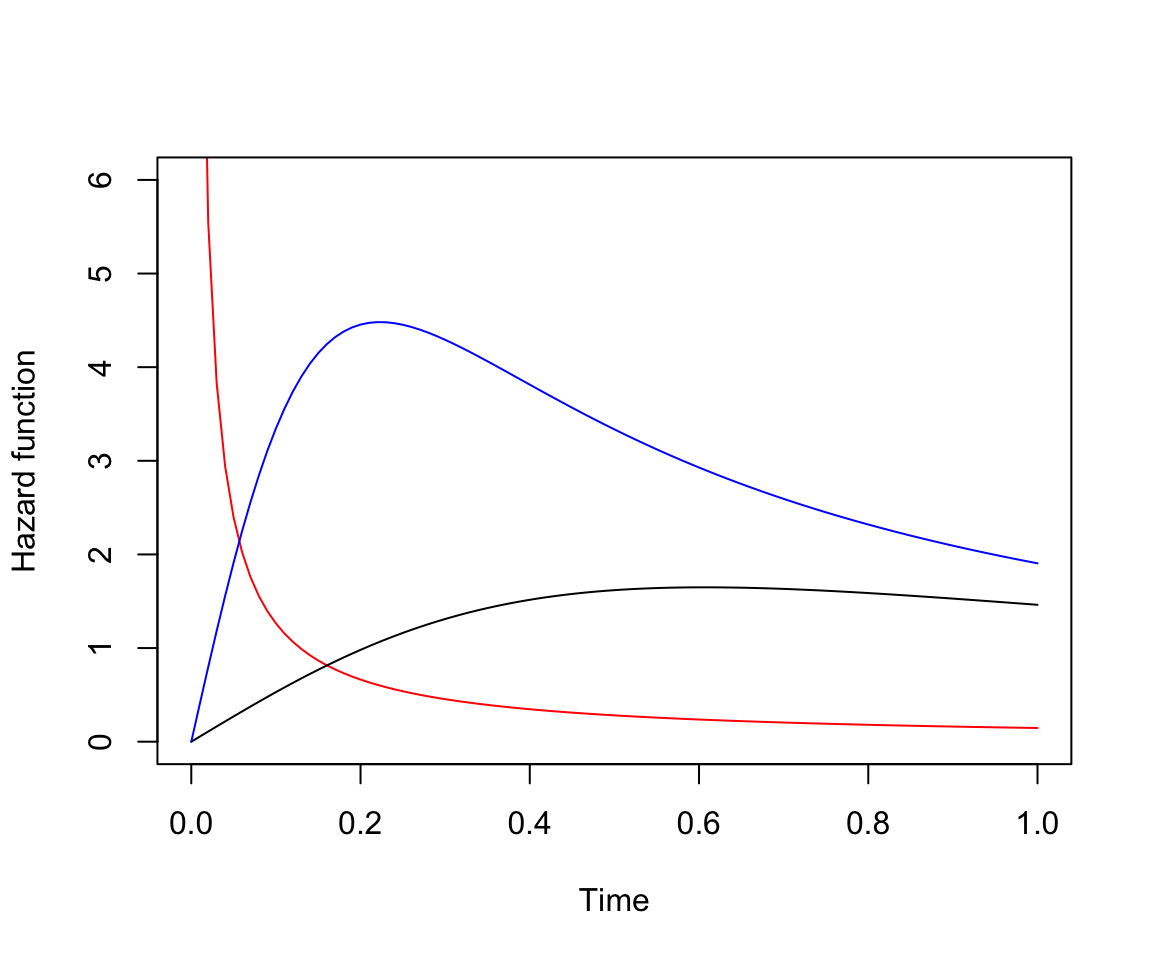
圖 85.5: Illustrations of the hazard function under a log-logistic distribution with different theta, and different shape (kappa)
在 Weibull 分布下,風險度只能隨着時間單調遞增或者遞減。但是,在對數邏輯分布下,風險度就可以跟隨時間有增有減。