第 98 章馬爾可夫鏈蒙特卡羅MCMC，圖形模型，BUGS語言

98.1 Markov Chain Monte Carlo 馬爾可夫鏈蒙特卡羅算法

98.1.1 爲什麼我們需要用計算機模擬算法(simulation methods)來進行貝葉斯統計推斷？

貝葉斯統計推斷是圍繞着事後概率分佈進行的:

\[ p(\mathbf{\theta}|x) \propto p(x|\mathbf{\theta})\times p(\mathbf{\theta}) \]

其中，\(\mathbf{\theta}\) 常常是一個很長的參數向量(vector of parameters) \(\mathbf{\theta} = \{ \theta_1, \theta_2, \dots, \theta_k \}\)，其中似然\(p(x|\mathbf{\theta})\)和先驗概率分佈\(p(\mathbf{\theta})\)一般都能找到相應的計算式，或者叫做閉合解形式(closed form)。可惜事後概率分佈 \(p(\mathbf{\theta}|x)\)就沒有這麼幸運，你會常常碰見無法在數學上獲得解析解的情況(analytically untractable)。

此時，我們又希望能夠獲得

某個或者某些參數的事後概率分布 \(p(\theta_i | x) = \int\int\dots\int p(\mathbf{\theta}|x)d\mathbf{\theta_{(-i)}}\) (where \(\mathbf{\theta_{(-i)}}\) denotes the vector of \(\theta\)s excluding \(\theta_i\))。
計算某個或者某些參數的事後概率分布的數學性質，特徵值如均值 \(= \int\theta_i p(\theta_i | x)d\theta_i\)，或者尾部的概率面積(tail areas) \(=\int_T^\infty p(\theta_i |x)d\theta_i\)等等。

我們無法獲得解析解 (analytical solution/closed solution) 的情況下，可以求助於數學上的數值解 (numerical solution/intergration)。

第二章 (Chapter 96) 我們已經見識過了蒙特卡羅模擬法可以用來從先驗概率分布，或者從閉合解形式(closed form)的事後概率分布中採樣計算的過程。如果我們可以把人類不可能完成的任務，也交給計算機來對無法獲取閉合解的事後概率分布做蒙特卡羅樣本採集的話，那麼貝葉斯統計學推斷就可以被推廣到幾乎任何一種模型，任何一種試驗設計中。

所以，我們的目的是希望從無法獲得閉合解形式的多維(多變量)事後概率分布\(p(\mathbf{\theta}|x)\)中採集樣本做計算機模擬實驗(simulation)。但是，現實中從這樣的事後概率分布中採集相互獨立(independent)的樣本，是不容易的一件事。反其道行之，科學家發現，從事後概率分布有依賴性的馬爾可夫鏈式樣本採集(dependent sampling from a Markov chain)，作爲一種穩態分布(stationary/equilibrium distribution)卻相對容易。

一連串的隨機變量 \(\theta^{(0)},\theta^{(1)},\theta^{(2)},\cdots\) 形成的馬爾可夫鏈，其重點在於 \(\theta^{(i + 1)} \sim p(\theta|\theta^{(i)}\)，也就是在 \(\theta^{(i)}\) 的條件下 \(\theta^{(i+1)}\) 和它之前的樣本 \(\theta^{(i - 1)},\cdots,\theta^{(0)}\)是獨立的。這樣的馬爾科夫鏈式採樣，需要特殊的方法來進行。美特羅波利斯-海斯廷斯(Metroplis-Hastings)算法(algorithm)是其中的一種。而吉布斯(Gibbs)採樣法是 Metropolis-Hastings 算法的一種特殊形態。吉布斯採樣法是從全條件分布(full conditional distributions)中產生一串馬爾科夫鏈的算法。我們下面來看看吉布斯採樣法的特徵和使用方法，其詳細的算法我們過後再來討論。

98.1.2 吉布斯採樣

假設，現在我們在給定了數據 \(x\) 之後，我們需要在關於它的一個未知參數的向量中\(\mathbf{\theta} = (\theta_1, \theta_2, \dots,\theta_k)\)採集事後概率分布樣本。那麼吉布斯採樣法的具體過程描述如下：

把未知參數向量分成不同的成分，最簡單的就是每個元素爲一個部分 \(\mathbf{\theta} = (\theta_1, \theta_2, \dots,\theta_k)\)；
給每個部分/參數選取一個起始值(starting/initial values) \(\theta_1^{(0)},\theta_2^{(0)},\dots,\theta_k^{(0)}\)；
然後:
從\(p(\theta_1|\theta_2^{(0)},\theta_3^{(0)},\dots,\theta_k^{(0)},x)\)中採集 \(\theta_1^{(1)}\)
從\(p(\theta_2|\theta_1^{(1)},\theta_3^{(0)},\dots,\theta_k^{(0)},x)\)中採集\(\theta_2^{(1)}\)
\(\vdots\)
從\(p(\theta_k|\theta_1^{(1)},\theta_2^{(1)},\dots,\theta_{k-1}^{(0)},x)\)中採集\(\theta_k^{(1)}\)
重復第3步 \(N\) 次，我們就可以獲得一串參數的事後分布樣本 \(\mathbf{\theta}^{(0)},\mathbf{\theta}^{(1)},\dots,\mathbf{\theta}^{(N)}\)。當 \(N\rightarrow\infty\) 我們就獲得了多維事後概率分布的一個樣本 \(p(\mathbf{\theta}|x)\)。

用只有兩個位置參數的向量來解釋就是：\(k = 2, \text{ i.e. } \mathbf{\theta} = (\theta_1, \theta_2)\)。下圖 98.1 展示了對兩個未知參數進行吉布斯採樣的一個過程：當我們先設定一組起始值 \(\mathbf{\theta}^{(0)}\)，之後從\(p(\theta_1|\theta_2^{(0)}, x)\)中採集\(\theta_1^{(1)}\)，然後再從 \(p(\theta_2|\theta_1^{(1)}, x)\)中採集\(\theta_2^{(1)}\)，這樣就獲得了樣本 \(\mathbf{\theta}^{(1)}\)。然後再重復相同搞得過程採集接下來的參數樣本。

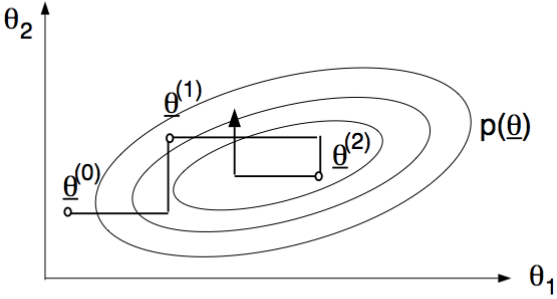
圖 98.1: Gibbs sampling with k = 2.

利用馬爾科夫鏈的性質，可以被證明的是當採樣達到無窮大 \(N\rightarrow\infty\)，無論起始樣本 \((\theta_1^{(0)},\theta_2^{(0)},\dots,\theta_k^{(0)})\) 如何採樣，最終產生的事後概率樣本 \(\mathbf{\theta}^{(0)},\mathbf{\theta}^{(1)},\dots,\mathbf{\theta}^{(N)}\) 將會收斂成爲真實的事後概率分布 \(p(\mathbf{\theta}|y)\)，所以確保了重復這個過程的次數是無窮大時，起初的一部分采样，\(N_0\)可作爲初始樣本，並且因爲通常一開始的採樣過程是不穩定的，而把他們從總體事後概率分布樣本中刨除，這個過程被叫做 burn in。最終可獲得樣本量爲 \(N-N_0\) 的事後概率分布樣本。

我们需要指出的是，這一採集事後概率分布樣本的方法之所以有用，是因爲條件事後概率分布(conditional posterior sampling)的採集，要比全事後概率分布(full posterior sampling)的採集要容易得多。否則，我們爲啥不直接從全事後概率分布中採樣呢。

簡單地說，比如我們需要同時對正態分布數據似然的均值，和方差兩個未知參數進行事後概率分布樣本的採集，兩個未知參數的事後概率分布需要用到復雜的微積分推導過程，但是我們知道已知均值時方差的事後概率分布，或者是已知方差時均值的事後概率分布，它們都比兩個未知參數時的計算和推導要簡單明了得多。

接下來我們來討論一下使用MCMC在貝葉斯統計學推斷中的實際應用和一些技巧。

98.1.3 初始值 initial values

MCMC過程需要對所有的未知參數先給出起始值(initial/starting values)。我們在使用BUGS進行貝葉斯統計學推斷時，可以利用先驗概率分布對各個未知參數隨機產生各自的起始值，但是這要建立在先驗概率分布是含有有價值的信息的前提下(informative priors)，如果我們只有一些聊勝於無的先驗概率分布(vague priors)，隨機從這樣的分布中產生起始值的話，很可能導致計算機選取很不恰當的起始值使得模型需要花很長的時間才能收斂，有些時候甚至導致計算機崩潰。這時候，統計學家的經驗是我們最好人爲地給模型中的未知參數設定幾個”合理”的起始值(separate reasonable initial values lists)，以防止不收斂或者計算機崩潰的情況出現。同時，我們也發現用戶如果給模型提供合理的起始值，也有助於鑑別模型收斂(convergence checking)。

在 BUGS 語言中，起始值可以直接寫在模型中，也可以寫在另外一個獨立的文件裏。需要明確指出的是，這些起始值是用來輔助 MCMC 採樣的，起始值並不是先验概率(initial values are not priors)。

98.2 使用 MCMC 時需要考慮的一些問題

在使用 MCMC 時有兩個主要的問題需要我們思考：

收斂時間：MCMC採集的樣本 \(\{\mathbf{\theta}^{(t)}\}\)，需要多久時間能夠到達或者接近事後概率分布 \(p(\mathbf{\theta}|x)\)。
效率：從採集的樣本 \(\mathbf{\theta}^{(t)}\) 中估計的參數是否在事後概率分布 \(p(\mathbf{\theta}|x)\) 中真的有效 (how well are functionals of \(p(\mathbf{\theta}|x)\) estimated from \(\{\mathbf{\theta}^{(t)}\}\))。

98.2.1 收斂時間

收斂時間，是我們關心的最主要的問題之一，我們在進行 MCMC 時要花多長時間才能使採集的樣本達到或者接近(數學上叫做收斂)真是的事後概率分布呢？換句話說，我們需要從採集的樣本中刨除掉多少一開始採集的不穩定的樣本呢(how do we know the number of “burn-in” iterations)？可以說沒有人能準確地給出一個答案。所以在檢查MCMC採樣是否收斂時，我們需要格外的小心。很多時候，沒有人能夠給出100%確定的答案說一條MCMC鏈達到了收斂，但是幸運地是，我們能準確地判斷沒有成功收斂的 MCMC 鏈。

檢查MCMC是否收斂，最常用的方法是視覺檢查，作出MCMC鏈式圖來輔助我們診斷。我們建議，使用多個不同的起始值，產生多個不同的 MCMC 樣本鏈來輔助診斷。當然，除了視覺診斷，另外還存在一些比較鏈內(within)和鏈間(between)方差的方法來進行收斂診斷的手段。但是，沒有哪種方法是萬無一失的。在 R 裏面，有一個很強大的包 coda，它被設計來把OpenBUGS的輸出結果 (output) 轉變成爲輸入對象 (input object)，利用R來便利地進行模型分析和診斷。許多對模型收斂程度的診斷，都會認爲未知參數的起始值是相對事後概率分布來說過度離散的。所以，建議在提供起始值的時候，每一個未知參數的起始值，都盡量爲每一個MCMC鏈給出幾個“合理”但差異較大(plausible but widely differing initial values)的起始值。

評估MCMC的收斂與否，一個比較實用的手段是雙保險的方法: 就是既從圖形視覺上來診斷產生的MCMC樣本鏈的收斂程度，也通過統計檢驗方法對收斂作收斂與否的統計學分析。當某些模型含有衆多的未知的參數的時候，你想對每一個未知參數的事後概率分佈的MCMC採樣是否收斂進行分析和檢驗可能是不太實際的，此時的常見手段是隨機選取衆多未知參數中幾個來分析其MCMC採樣結果的收斂與否。

我們的選擇包括：

把MCMC事後概率分布採樣過程的整個歷史(history)痕跡(trace)全部繪制出來-不同起始值的同一個未知參數的MCMC鏈是否都給出了相對穩定的歷史痕跡？他們是否有合理的相互重疊(overlapping)？
檢查自我相關程度(autocorrelation)-過高的自相關暗示收斂過程較慢。(high autocorrelation is a symtom of slow convergence)。
看Gelman-Rubin收斂統計量-它通過比較MCMC鏈內方差(within variability)和鏈間方差(between variability)來評估MCMC鏈是否達到收斂。

98.2.1.1 視覺檢驗方法

視覺檢驗方法是一種十分有效的輔助鑑別MCMC樣本鏈是否收斂的手段。常用的方法是使用幾個不同，且合理的起始值進行MCMC採樣運算，看他們是否最終都收斂到相同的位置。通常我們會把採集的 \(\theta^{(i)}\) 樣本和 \(i\) (也就是採樣次數) 做圖，如果順利達到收斂，圖形應該顯示爲隨機出現在一條直線上下附近的散點圖。

在BUGS軟件裏，通常有兩種方法可以供用戶查看未知參數的MCMC樣本鏈的歷史痕跡(history trace)：

實時觀察MCMC樣本採集的歷史痕跡。 (只能在windows下進行，需要用到OpenBUGS的窗口)
MCMC樣本採集結束以後把採集的未知參數事後樣本的歷史痕跡一次性全部繪制出來。

繪制歷史痕跡時用不同顏色來表示不同起始值的MCMC鏈會更加有助於我們在圖形上識別出MCMC鏈是否分別都達到了令人滿意的模型收斂，互相的重疊程度也能一目了然。

至於(Brooks-)Gelman-Rubin (BGR)診斷收斂統計量，它的使用前提是必須使用合理且差異較大的不同起始值（至少兩個）。

98.2.2 模型效率 efficiency of MCMC

一旦你認爲MCMC採集的樣本鏈已經達到收斂於事後概率分布。接下來要做的是繼續MCMC樣本採集，採集的事後概率分布樣本越多，事後概率推斷就越精確。通常一個表現良好的事後概率分布，我們的經驗是4000個左右的獨立樣本產生的95%可信區間能夠給出94%-96%實際的事後概率分布(actual posterior probability) (Raftery and Lewis 1992)。但是實際上MCMC採集的樣本鏈是高度自相關的(autocorrelated)，因此實際有效的樣本量會少於真實的樣本量。(effective sample size < actual sample size)

計算事後概率分布對未知參數的估計的精確度的方法之一，是給每一個未知參數計算蒙特卡羅標準誤(Monte Carlo standard error)。它是對MCMC樣本參數均值和真實事後均值之間差的估計(estimate of the difference between the mean of the sampled values, which we are using as our estimate of the posterior mean for each parameter, and the true posterior mean.)。

MCSE (Monte Carlo Standard Error) 等於未知參數的事後樣本均值的標準誤。此時，事後樣本均值被當做是事後期望值的理論取值的一個估計 (an estimate of the theoretical posterior expectation) \(E(\theta|y)\)。

如果採集的樣本是相互獨立的，那麼\(\text{MCSE}^{ind} = \frac{s}{\sqrt{N}}\) 其中，\(s = \text{posterior SD}\) 參數\(\theta\)的事後樣本標準差，\(N\) 是採集的事後樣本的樣本量。但是我們真正能採集到的樣本是自相關樣本(autocorrelated samples)，自相關樣本的\(\text{MCSE}^{ac} > \text{MCSE}^{ind}\)。

一個有自相關的MCMC鏈的有效樣本量 (effective sample size)\(N^*\)可以這樣估計：

\[ N^* = (\frac{s}{\text{MCSE}^{ac}})^2 \]

所以，如果：

\(\text{MCSE}^{ac} \approx 0.05s \Rightarrow N^* \approx 1/0.05^2 = 400\);
\(\text{MCSE}^{ac} \approx 0.015s \Rightarrow N^* \approx 1/0.015^2 = 4444\);
\(\text{MCSE}^{ac} \approx 0.01s \Rightarrow N^* \approx 1/0.01^2 = 10000\);

由事後樣本的標準差和蒙特卡羅標準誤之間的關系可見，基本上MCMC鏈達到收斂以後，你需要重復MCMC採樣的次數，也就是採集的事後分布樣本量的大小要使得蒙特卡羅標準誤小於事後樣本標準差的1/100才能基本滿足要求。未知參數的事後估計和總結也就是要建立在有效樣本量至少爲10000或更多的基礎之上。

98.3 BUGS 軟件

你完全可以另闢蹊徑在STATA或者R裏面寫下吉布斯採樣的算法，但是這並不簡單。幸好，許多軟件已經能夠幫助我們規避掉寫吉布斯採樣算法這一複雜的過程。

BUGS全稱是 Bayesian inference Using Gibbs Sampling。它是用來描述貝葉斯統計學模型的計算機語言。有三種流行的統計學軟件都使用BUGS語言來描述貝葉斯統計學模型，他們分別是 WinBUGS，OpenBUGS，和 JAGS。他們的語法十分接近R的語法，甚至可以直接在R的環境下運行(正如我這本書中在R裏連接JAGS運算貝葉斯統計推斷一樣)。

WinBUGS 1.4.3是一個穩定的貝葉斯統計學軟件，但是它已經不再更新，也沒有再跟進開發。也正如其名字暗示的那樣，它能且只能運行在瘟倒死(windows)機器上。你可以從它的網站上下載並免費使用之: https://www.mrc-bsu.cam.ac.uk/software/bugs/the-bugs-project-winbugs/。

OpenBUGS是開源的，且能夠在Linux機器上無縫運行。它也有自己的GUI(只有在瘟倒死上才有的功能)，讓你實現用鼠標點擊也能完成貝葉斯統計學分析。它的主要網站是http://www.openbugs.net/w/Downloads。

JAGS的全稱是 Just Another Gibbs Sampler，開發者是 Martyn Plummer。它沒有任何GUI，只能通過命令行來執行運算。

其他著名的軟件還有 Stan。它也是開源的自由軟件。

98.4 圖形模型 statistical graphical models - Directed Acyclic Graphs (DAGs)

在統計學模型中我們常常默認指定一些隨機變量之間的邏輯關系，這樣的邏輯關系可以用圖形來表示：

節點 nodes：用來表示變量(variables)；
連接線 links：用來表示變量之間的邏輯依賴關系(dependence association)。

帶方向的連接線 (directed links)被用來表示邏輯依賴關系的方向(natural ordering of the dependence association)。其實這連接線所帶的方向本身就是回歸模型中表示預測變量和結果變量之間的依賴關系。貝葉斯統計學中常用的有向無環圖 (directed acyclic graphs, DAGs)，是我們常用的輔助建立貝葉斯模型的示意圖。

例如一個描述吸煙，肥胖和心髒病發病可能的關系的的有向無環圖如下圖 98.2。途中帶方向的連線（箭頭）表示預測變量和結果變量之間的依賴關系。

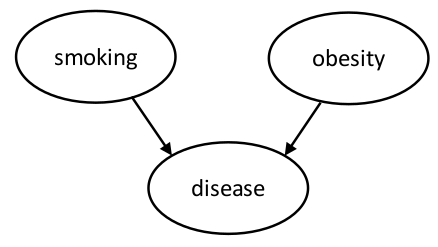
圖 98.2: DAG for heart disease example

98.4.1 條件獨立的概念 conditional independence concept

在概率論入門(Chapter 1)中學習過獨立的概念：

\[ p(Y,X) = p(Y)p(X) \]

我們說 \(X,Y\) 以條件 \(Z\) 獨立如果他們滿足：

\[ p(X,Y|Z) = p(Y|Z)p(X|Z) \]

條件獨立的關系可以用下面的有向無環圖 98.3 來表示：

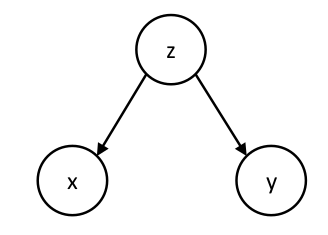
圖 98.3: DAG for conditional independence

基因型例子 genotype example:如果 \(X,Y\) 分別是同一個家庭中的兩個孩子的基因型，\(Z\)是其父母的基因型。那麼兩個孩子之間的基因型就是以父母的基因型爲條件獨立的關系: \(p(X,Y|Z) = p(Y|Z)p(X|Z)\)。如果沒有父母親基因型的條件，兩個孩子的基因型就不互相獨立，而是相關的（很顯然因爲他們是親兄弟/妹）。

在有向無環圖的術語中，一個變量的Parent(父/母)指的是有向連線指向該變量的最近的那個變量，反過來這個被指向的變量就被叫做Child(子)。所以如果從變量 \(\alpha\) 存在指向 \(\beta\) 的箭頭連線，那麼 \(\alpha\) 被叫做 \(\beta\) 的父/母(parent)，\(\beta\) 被叫做 \(\alpha\) 的子(child)。

硬幣例子 coin example:如果一枚硬幣正面朝上或者反面朝上的概率分別是 \(p(H), p(T)\)，那麼令 \(p(H) = \theta = 1 - p(T)\)，如果兩次投擲硬幣試驗的結果分別是 \(X, Y\)，那麼 \(X,Y\) 就是以 \(\theta\) 爲條件的獨立事件: \(p(X,Y|\theta) = p(Y|\theta)p(X|\theta)\)。這裏的 \(\theta\) 在貝葉斯統計學的環境下不是固定不變的，而是一個隨機的未知參數。

條件獨立是一個十分重要的概念，因爲它爲\(X,Y,Z\)三個未知參數的聯合分布(joint distribution)提供了十分有用的因式分解理論依據：

\[ p(X,Y,Z) = p(Y|Z)p(X|Z)p(Z) \]

因爲，即使使用計算機進行模擬實驗 (simulation)，從條件分布\(p(Y|Z), p(X|Z)\)中採集事後概率分布樣本，也比從 \(p(X,Y,Z)\) 中直接採集樣本要容易進行得多。

一般地，一個含有許多個變量節點(nodes)的向量的聯合分布可以寫作：

\[ p(V) = \prod_{v\in V} p(v|\text{parents}[v]) \]

下圖98.4給出的一個較爲復雜的 DAG 模型，其實它沒有看起來那麼復雜，有了條件獨立的概念，我們可以方便地把它的聯合分布進行因式分解：

\[ p(V) = p(A)p(F)p(B|A)p(C|A)p(E|A,F)p(D|B,C) \]

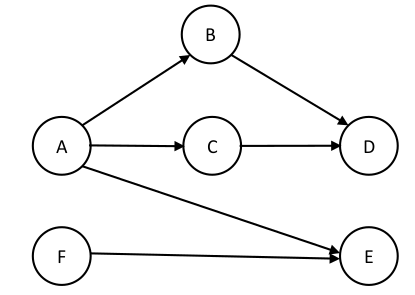
圖 98.4: More complex DAG for conditional independence

BUGS軟件也是利用這一概念來進行復雜的事後概率分布模型的計算，例如上述的模型中，

\[ p(E|A,B,C,D,F) = p(E|A,F) \]

98.5 BUGS language

在 BUGS 軟件提供的手冊裏有對 BUGS 語言更加詳盡的介紹，這裏我們只是對其精要部分做簡單概括的介紹。

98.5.1 節點的種類 types of nodes

在 BUGS 環境下，每個變量或者參數都被叫做一個節點。它主要被分爲兩類：

隨機節點 (stochastic nodes)：需要我們給出它們分布的描述。一個波浪線 ~ 被用來幫助我們描述這些隨機節點的分布，例如 r ~ dunif(a, b) 的含義就是，在區間 \([a,b]\) 內，\(r\)服從均一分布。
邏輯節點 (logical nodes)：則表示的是對節點和節點之間關系的定義，它常常是一個方程，用 <- 來輔助定義。例如，m <- alpha + beta*x 定義的是 \(m\) 和 \(\alpha, \beta, x\) 節點之間的數學關系。

98.5.2 分布的標記法

BUGS語言中常用的分布和其對應的標記法歸納如下:

Expression	Distribution	Usage
`dbin`	binomial	`r ~ dbin(p,n)`
`dnorm`	normal	`x ~ dnorm(mu, tau)`
`dpois`	Poisson	`r ~ dpois(lambda)`
`dunif`	uniform	`x ~ dunif(a, b)`
`dgamma`	gamma	`x ~ dgamma(a, b)`

要注意的是，這裏的正態分布的參數是均值 mu，和精確度 precision tau:

\[ \text{precision} = \frac{1}{\text{variance}} = \frac{1}{sd^2} \]

另外，在 BUGS 語言中，我們無法在指定分布時給參數使用方程，這種時候必須做的是分步驟來寫模型：

y ~ dnorm(mu, tau); mu <- a + b*x

不能被寫作：

y ~ dnorm(a+b*x, tau)

98.5.3 Arrays and loops

當有些模型需要有重復執行的步驟的時候，可以使用排列 (arrays) 或者循環 (loops) 的方式來寫你的BUGS模型。例如下面的代碼用來表示在長度或者人數爲 \(m\) 的數據中循環相同的步驟，其中n, p, r都是具有相同長度的向量：

for (i in 1:m){ # loop over m individuals
  r[i] ~ dbin(p[i], n[i]) 
  p[i] ~ dunif(0, 1)
}

所有被包括在大括號 {} 裏面的命令都跟着變量 i 被從 1 開始重復相同的步驟直至第 m 個對象。

98.5.4 常用的方程

BUGS 建立貝葉斯模型你會常用到的方程有：

p <- step(x - 0.7): 當 \(x\geqslant0.7\)時\(=1\)，反之 \(=0\)；類似這樣的方程可以拿來監測 p 這個節點，如果取它的均值，我們就得到 \(x\geqslant0.7\) 的概率。
p <- equals(x, 0.7): 當 \(x = 0.7\)時\(=1\)，反之 \(=0\)。
tau <- 1/pow(s, 2): 這是用來給變量節點 s 加指數方程的命令等價於 \(\tau = \frac{1}{s^2}\)。
s <- 1/sqrt(tau): 等價於 \(s = \frac{1}{\sqrt{\tau}}\)。

在BUGS手冊的 “Model Specification/Logical nodes” 章節有更多對不同方程命令的描述。

一般地，方程的定義要出現在 <- 的右邊，例如 totalx <- sum(x[])，但是並不是全部都必須如此的，例如在廣義線性回歸模型(GLM)中，鏈接方程 (link function) 是允許出現在箭頭的左邊的：

logit(p[i]) <- a +b*x[i]
log(m[i]) <- c + d*y[i]

mean(p[])的含義是對 p 的所有成分取均值，如果是 mean(p[m:n])，則是對數列 p 中成分排序在 m,n 之間取均值，忽略掉其前後的元素。相似的概念也適用於 sum(p[]) 命令。

98.6 爲BUGS model模型準備格式正確的數據

OpenBUGS/JAGS 只能接受格式爲 R/S-plus 的，或者是整理成形狀爲長方形的文字格式數據。例如，名叫GREAT的臨牀試驗數據中，

在家中接受治療的患者人數是163，其中13例死亡；
在醫院內接受治療的患者人數是148，其中23例死亡。

這個模型可以用循環寫作：

for(i in 1:2){ # loop through the arms
    deaths[i] ~ dbin(p[i], n[i]) # likelihood for each arm
    p[i]  ~ dbeta(alpha, beta)  # same prior for each arm
}

這個模型的標記中， deaths[i] 表示第 \(i\) 組對象中死亡人數，n[i] 則表示第 \(i\) 組實驗對象中的總人數。而 p[i] 則代表了第 \(i\) 組對象中實驗對象死亡的概率。

那麼這個數據應該用怎樣的語言來描述才合理呢？

如果用長方形格式數據，要寫作：

n[] deaths[]
163 13
148 23
END

這種格式中，第一行需要給出變量名稱，每一列是變量相對應的數據，變量名稱也必須和模型中的變量名稱相匹配。在數據最後一行則需要用END來結束，並且接着要有一個空行。（所以在這樣的數據格式中最後一行必須是空行）

R/S-plus格式的數據，我們已經很熟悉了，可以寫作：

list(n = c(163, 148), 
     deaths = c(13, 23))

OpenBUGS同時還允許你給模型加載多個數據文件，你如果願意的話，可以把不同格式的數據混合使用，一起加載在模型裏運算。

98.7 Practical Bayesian Statistics 04

這一次練習題的主要目的是，通過使用OpenBUGS/JAGS來思考，它是如何從非共軛模型的事後概率分布中採集MCMC樣本的。這個過程和從共軛模型的事後概率分布中採樣有哪些不同。

思考前一次，第三章的課後練習題裏的(Chapter 97.6)新藥試驗的例子。還是用這個場景，但是我們這次實施8個不同的試驗，\(i = 1,\dots,8\)，其中第\(i\)次試驗有 \(n_i\) 名患者，其中 \(y_i\) 名患者的治療被認爲有顯著療效。每次試驗中的 \(n_i\) 名患者都給予相同劑量\(x_i\)，但是不同於其他次試驗時的使用劑量的藥物。此時我們把注意力轉到，評估治療有效百分比 \(\theta_i\)，和劑量\(x_i\)之間的關系上來。

一種方法是，我們可以對這個數據擬合一個邏輯回歸模型，在貝葉斯統計學中，邏輯回歸模型的擬合方式如下：

\[ \begin{aligned} y_i & \sim \text{Binomial}(\theta_i, n_i) \\ \text{logit}(\theta_i) & = \beta_0 + \beta_1 x_i \end{aligned} \]

其中 \(\text{logit}\) 轉換是方便地把 \(0\sim1\) 之間的百分比變量轉化成爲 \(-\infty, +\infty\) 變量的鏈接方程。另外，貝葉斯統計學模型中，我們需要給所有模型中出現的未知參數，提供一個先驗概率分布。在上面這個模型中，我們給有效百分比 \(\theta_i\) 定義了一個回歸方程式，因此，我們需要給這個回歸方程式的回歸系數(regression coefficients)指定先驗概率分布。我們先使用模糊的，沒有太多信息的先驗概率分布，例如均一分布：

\[ \begin{aligned} \beta_0 & \sim \text{Uniform}(-100, 100)\\ \beta_1 & \sim \text{Uniform}(-100, 100) \end{aligned} \]

1.首先，用第三章練習題中的新藥試驗模型，使用 \(\text{beta}(1, 1)\) 作爲 \(\theta\)的先驗概率分布（已知\(\text{beta}(1, 1)\)其實等價於一個均一分布）。設定監測未知參數 theta，執行1000次MCMC運算之後，繪制 theta 的歷史痕跡。下列模型代碼保存爲 MCdrugPractical04.txt 文檔。

# original conjugate drug model with uniform beta(0,1) prior on theta

model{
    theta ~ dbeta(1,1)     # prior distribution
    y     ~ dbin(theta, 20)# sampling distribution for 20 observed patients
    #y    <- 15
}

# Codes for R2JAGS

Dat <- list(
y = c(15)                    
)

# fit use R2jags package

post.jags <- jags(
  data = Dat,
  parameters.to.save = c("theta"),
  n.iter = 1100,
  model.file = paste(bugpath, 
                     "/backupfiles/MCdrugPractical04.txt", 
                     sep = ""),
  n.chains = 1,
  n.thin = 1,
  n.burnin = 100,
  progress.bar = "none")

## Compiling model graph
##    Resolving undeclared variables
##    Allocating nodes
## Graph information:
##    Observed stochastic nodes: 1
##    Unobserved stochastic nodes: 1
##    Total graph size: 4
## 
## Initializing model

print(post.jags)

## Inference for Bugs model at "/Users/chaoimacmini/Downloads/LSHTMlearningnote/backupfiles/MCdrugPractical04.txt", fit using jags,
##  1 chains, each with 1100 iterations (first 100 discarded)
##  n.sims = 1000 iterations saved
##          mu.vect sd.vect  2.5%   25%   50%   75% 97.5%
## theta      0.725   0.094 0.536 0.662 0.734 0.793 0.885
## deviance   4.158   1.281 3.197 3.294 3.709 4.473 7.802
## 
## DIC info (using the rule, pD = var(deviance)/2)
## pD = 0.8 and DIC = 5.0
## DIC is an estimate of expected predictive error (lower deviance is better).

下面我們來看題幹中的邏輯回歸模型的BUGS版本：

model {
       for( i in 1 : N ) { # loop thorugh experiments
            y[i] ~ dbin(theta[i],n[i])
           logit(theta[i]) <- beta0 + beta1 * x[i]    
       }
       # priors
       beta0 ~ dunif(-100, 100)
       beta1 ~ dunif(-100, 100)
}

試驗獲得觀察數據如下：

list(y = c(1, 3, 6, 8, 11, 15, 17, 19), 
     n = c(20, 20, 20, 20, 20, 20, 20, 20), 
     x = c(30, 32, 34, 36, 38, 40, 42, 44), 
     N = 8 )

嘗試使用JAGS/OpenBUGS來跑這個模型。記得你需要把數據加載到軟件裏面去。

# Codes for R2JAGS


Dat <- list(
     y = c(1, 3, 6, 8, 11, 15, 17, 19), 
     n = c(20, 20, 20, 20, 20, 20, 20, 20), 
     x = c(30, 32, 34, 36, 38, 40, 42, 44), 
     N = 8 
)

# fit use R2jags package

post.jags <- jags(
  data = Dat,
  parameters.to.save = c("beta0", "beta1", "theta[6]"),
  n.iter = 1100,
  model.file = paste(bugpath, 
                     "/backupfiles/logistic-reg-model.txt", 
                     sep = ""),
  n.chains = 1,
  n.thin = 1,
  n.burnin = 100,
  progress.bar = "none")

## Compiling model graph
##    Resolving undeclared variables
##    Allocating nodes
## Graph information:
##    Observed stochastic nodes: 8
##    Unobserved stochastic nodes: 2
##    Total graph size: 53
## 
## Initializing model

print(post.jags)

## Inference for Bugs model at "/Users/chaoimacmini/Downloads/LSHTMlearningnote/backupfiles/logistic-reg-model.txt", fit using jags,
##  1 chains, each with 1100 iterations (first 100 discarded)
##  n.sims = 1000 iterations saved
##          mu.vect sd.vect    2.5%     25%     50%    75%  97.5%
## beta0    -11.304   1.716 -14.542 -12.657 -11.225 -9.850 -8.262
## beta1      0.306   0.046   0.224   0.267   0.303  0.341  0.396
## theta[6]   0.715   0.049   0.617   0.683   0.717  0.749  0.805
## deviance  26.937   2.666  23.793  24.816  26.298 28.385 33.116
## 
## DIC info (using the rule, pD = var(deviance)/2)
## pD = 3.6 and DIC = 30.5
## DIC is an estimate of expected predictive error (lower deviance is better).

對未知參數，也就是邏輯回歸的回歸系數 beta0, beta1，和第六次試驗的治療成功百分比 theta[6] 設定監測追蹤其採樣軌跡。試着執行1000次MCMC採樣，把這三個跟蹤的未知參數的採樣歷史軌跡繪制下來。

#### PLOT THE MCMC CHAINS:
mcmcplots::traplot(post.jags, c("beta0", "beta1", "theta[6]"))

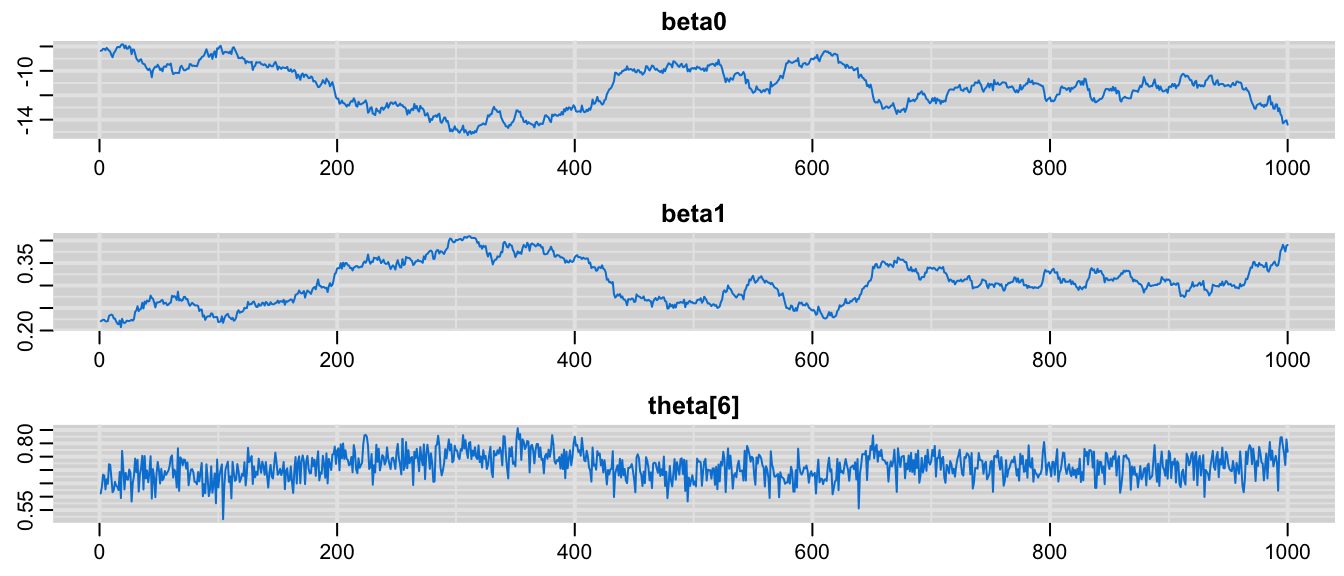
圖 98.5: History plot showing 1000 samples of beta0

對這三個位置變量的採樣歷史繪制痕跡圖之後，你發現每個參數期初的一些採樣是十分不穩定的，有很大的變動(variability)。

接下來，我們給上面同一個邏輯回歸模型增加另一條MCMC採樣鏈，重復跑相同的模型1000次，繪制同樣是這三個未知參數的事後分布MCMC採樣歷史痕跡圖。

# fit use R2jags package

post.jags <- jags(
  data = Dat,
  parameters.to.save = c("beta0", "beta1", "theta[6]"),
  n.iter = 1000,
  model.file = paste(bugpath, 
                     "/backupfiles/logistic-reg-model.txt", 
                     sep = ""),
  n.chains = 2,
  n.thin = 1,
  n.burnin = 0,
  progress.bar = "none")

## Compiling model graph
##    Resolving undeclared variables
##    Allocating nodes
## Graph information:
##    Observed stochastic nodes: 8
##    Unobserved stochastic nodes: 2
##    Total graph size: 53
## 
## Initializing model

mcmcplots::traplot(post.jags, c("beta0", "beta1", "theta[6]"))

圖 98.6: History plot showing 1000 samples of beta0, beta1, and theta[6]

使用兩個不同的起始值作爲MCMC的採樣起點時，每個未知參數分別獲得兩條不同顏色的歷史痕跡圖。和之前只有一條MCMC採樣鏈時一樣，採樣的起始部分(大約100次左右)都有一些不穩定的值。等到100次採樣過後，我們發現每個參數的採樣結果都趨向於比較穩定，也就是方差，變化小了很多。但是藍色鏈，紅色鏈一直到200-300次採樣之後才逐漸互相交叉重疊。下面的圖把起初的500次採樣刨除了之後重新對每個未知參數的MCMC採樣繪制歷史痕跡。

# samplesHistory("*", mfrow = c(3,1), beg = 501, ask = FALSE)
Simulated <- coda::as.mcmc(post.jags)
ggSample <- ggs(Simulated)

ggSample %>% 
  filter(Iteration >= 500 & Parameter %in% c("beta0", "beta1", "theta[6]")) %>% 
  ggs_traceplot()

圖 98.7: History plot showing 1000 samples of beta0, beta1, and theta[6], iteration between 501-1000

500-1000次之間的隨機採樣被放大了觀察之後，我們發現 beta0, beta1 的兩條MCMC鏈條的重疊程度並不理想，不像theta[6]那樣呈現令人滿意地重疊，兩條採樣鏈上下扭動，且在一些地方差異較大。

繪制每個參數的MCMC鏈的自相關圖 (autocorrelation)，下面的圖中只繪制了500-1000次範圍內採樣的自相關圖。

ggSample %>% 
  filter(Iteration >= 500 & Parameter %in% c("beta0", "beta1", "theta[6]")) %>% 
  ggs_autocorrelation()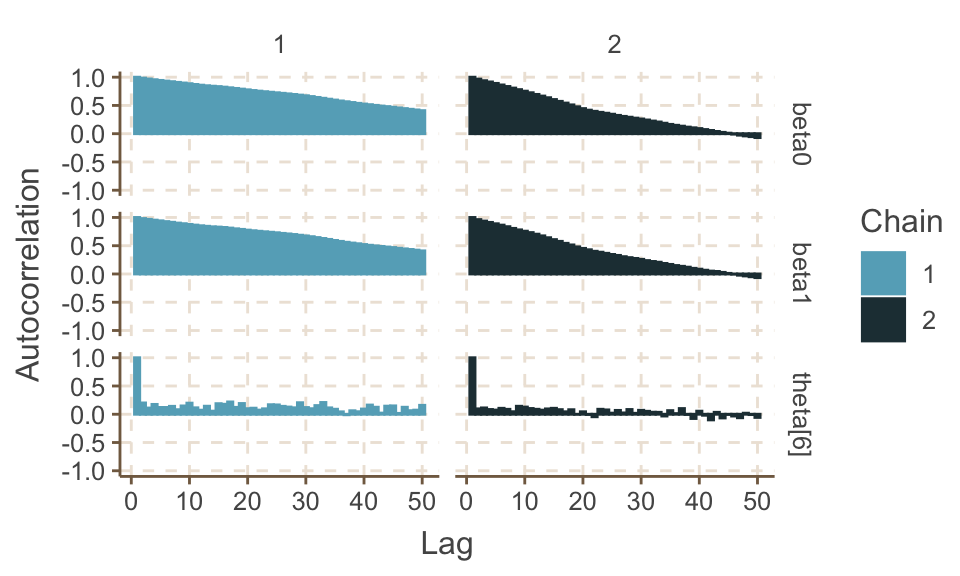

圖 98.8: Autocorrelation plot for beta0

其中 theta[6] 可以在視覺上認爲這些樣本大致上沒有自相關。但是 beta0, beta1 的自相關圖提示相隔50次以上的採樣之間仍然有較強的，不能被忽視的自相關。這一點在 beta0, beta1各自的歷史痕跡圖中也能看出來因爲他們各自的痕跡圖提示採樣時的跳躍並不顯著，相對照的， theta[6]的採樣的跳躍就比較顯著，反映了這個未知參數事後概率分布採樣時的連續互相獨立性較好(near-independence of the values being sampled at consecutive iterations.)。

重新在OpenBUGS裏跑這個邏輯回歸模型，這一次，嘗試自己給 beta0, beta1 設置起始值。然後更新模型，採集MCMC鏈樣本10000次。這次嘗試同時使用繪制歷史痕跡圖（視覺檢查），和計算Brooks-Gelman-Rubin診斷參數及其圖示來判斷事後概率分布採樣是否達到收斂。你能判斷這個模型需要拋出掉多少一開始採集的樣本嗎(burn-in)？

Dat <- list(
     y = c(1, 3, 6, 8, 11, 15, 17, 19), 
     n = c(20, 20, 20, 20, 20, 20, 20, 20), 
     x = c(30, 32, 34, 36, 38, 40, 42, 44), 
     N = 8 
)

# fit use rjags package

# inits <- function (){
#   list (beta0=rnorm(1), beta1=runif(1) )
# }

post.jags <- jags(
  data = Dat,
  # inits = inits,
  parameters.to.save = c("beta0", "beta1", "theta[6]"),
  n.iter = 5000,
  model.file = paste(bugpath,
                     "/backupfiles/logistic-reg-model.txt",
                     sep = ""),
  n.chains = 2,
  n.thin = 1,
  n.burnin = 0,
  progress.bar = "none")

mcmcplots::traplot(post.jags, c("beta0", "beta1", "theta[6]"))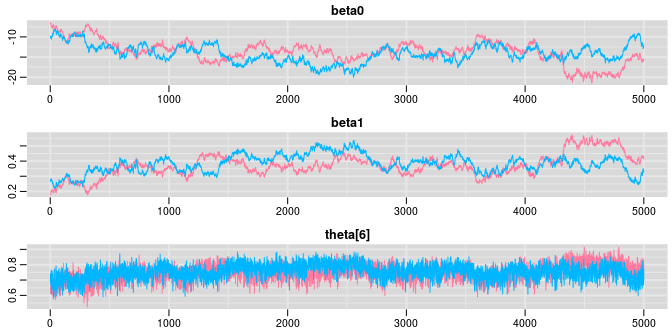

圖 98.9: History plots based on first 10000 iterations.

Simulated <- coda::as.mcmc(post.jags)
# postsamples <- buildMCMC("*")
gelman.diag(Simulated)

## Potential scale reduction factors:
## 
##          Point est. Upper C.I.
## beta0          3.15       7.35
## beta1          3.15       7.29
## deviance       1.82       3.36
## theta[6]       1.42       2.25
## 
## Multivariate psrf
## 
## 2.22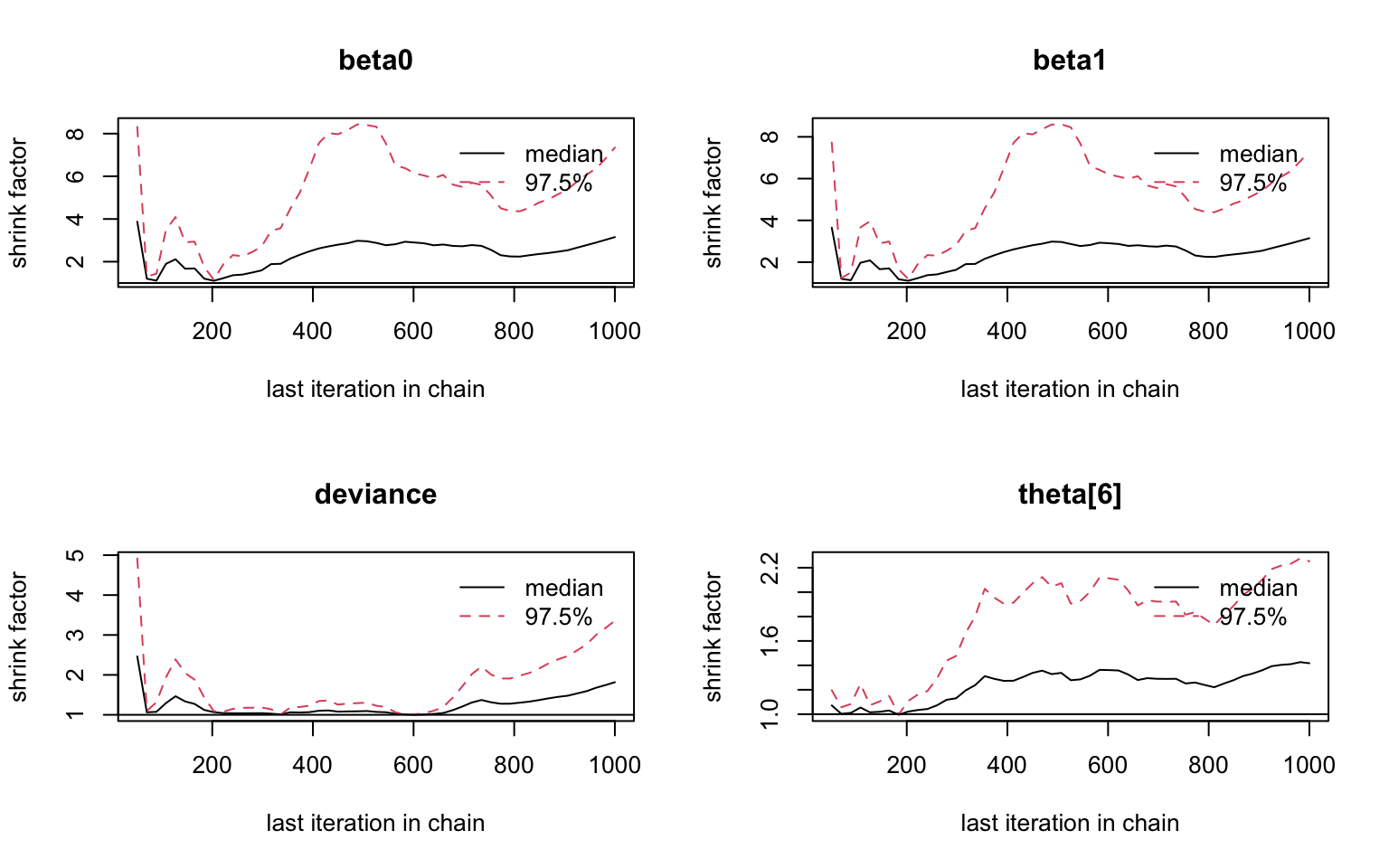

gelman.plot(Simulated)

圖 98.10: Brooks-Gelman-Rubin diagnostic graph

從Gelman.plot的圖形可以看出，在2000次及以上的採集樣本過後，基本上應該可以認爲採集的樣本收斂於事後概率分布。

確認了你想要刨除的初始樣本量(burn-in)，繼續再進行MCMC採樣直到獲得1,000,000個事後概率分布樣本。此時你對獲得的事後概率分布樣本量提供的參數估計精確度滿意否？嘗試報告此時獲得的參數們的事後均值，及其95%可信區間。

Dat <- list(
     y = c(1,   3,  6,  8, 11, 15, 17, 19), 
     n = c(20, 20, 20, 20, 20, 20, 20, 20), 
     x = c(30, 32, 34, 36, 38, 40, 42, 44), 
     N = 8 
)

# inits <- function (){
#   list (beta0=rnorm(1), beta1=runif(1) )
# }

post.jags <- jags(
  data = Dat,
  # inits = inits,
  parameters.to.save = c("beta0", "beta1", "theta[6]"),
  n.iter = 502000,
  model.file = paste(bugpath,
                     "/backupfiles/logistic-reg-model.txt",
                     sep = ""),
  n.chains = 2,
  n.thin = 1,
  n.burnin = 2000,
  progress.bar = "none")

## Compiling model graph
##    Resolving undeclared variables
##    Allocating nodes
## Graph information:
##    Observed stochastic nodes: 8
##    Unobserved stochastic nodes: 2
##    Total graph size: 53
## 
## Initializing model

Compiling model graph
   Resolving undeclared variables
   Allocating nodes
Graph information:
   Observed stochastic nodes: 8
   Unobserved stochastic nodes: 2
   Total graph size: 53

Initializing model

Inference for Bugs model at "/home/ccwang/Documents/LSHTMlearningnote/backupfiles/logistic-reg-model.txt", fit using jags,
 2 chains, each with 502000 iterations (first 2000 discarded)
 n.sims = 1000000 iterations saved
         mu.vect sd.vect    2.5%     25%     50%     75%   97.5%  Rhat n.eff
beta0    -13.892   2.090 -18.257 -15.237 -13.788 -12.449 -10.042 1.001  3900
beta1      0.375   0.056   0.272   0.337   0.373   0.412   0.493 1.001  3100
theta[6]   0.752   0.048   0.652   0.720   0.754   0.786   0.841 1.001 10000
deviance  25.722   2.020  23.760  24.283  25.095  26.499  31.199 1.001  9600

For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).

DIC info (using the rule, pD = var(deviance)/2)
pD = 2.0 and DIC = 27.8
DIC is an estimate of expected predictive error (lower deviance is better).

繪制此時beta0,beta1的自相關圖。

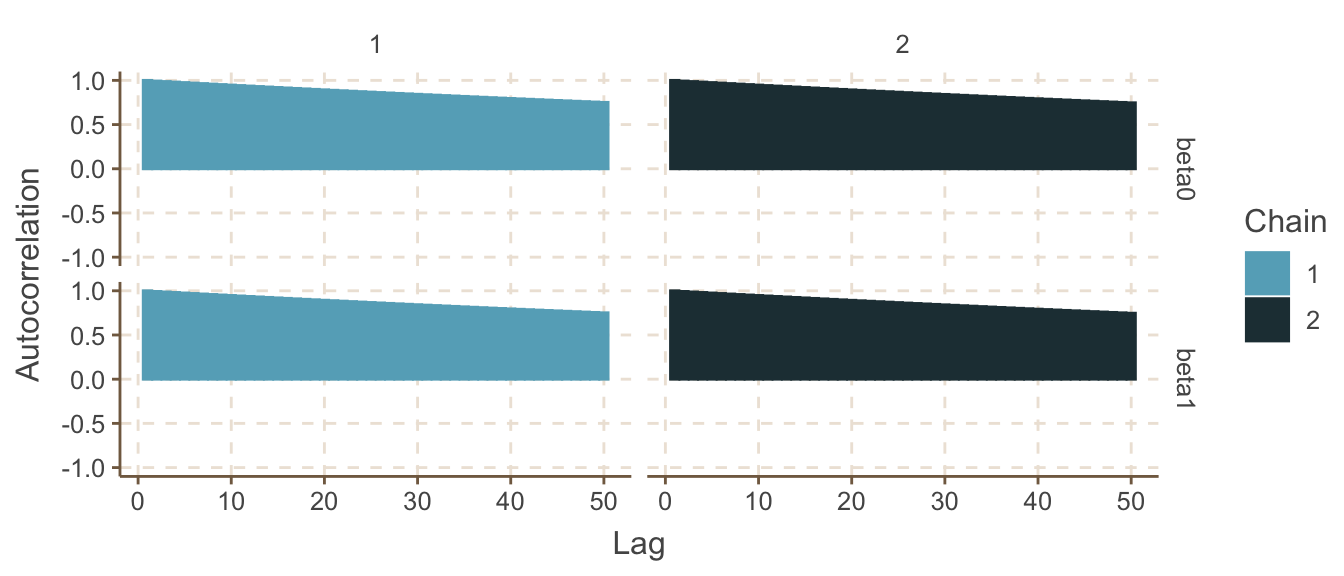
圖 98.11: Autocorrelation plot for beta0

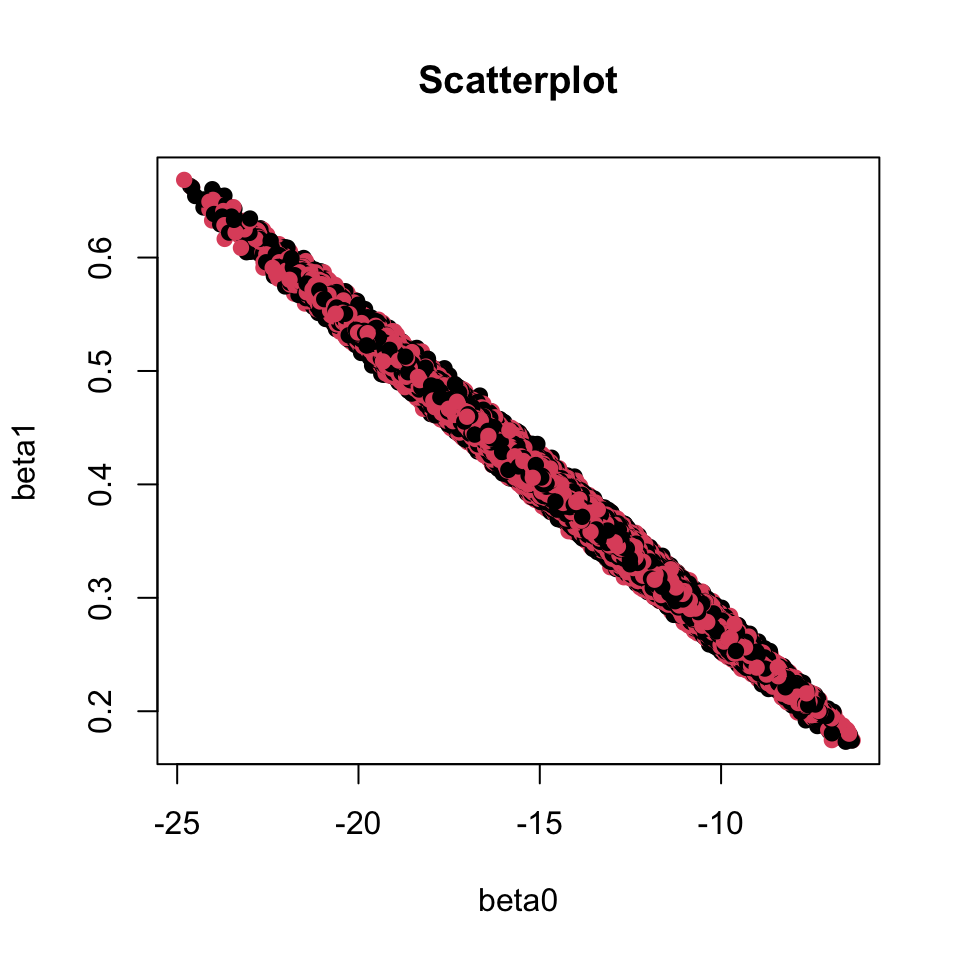
圖 98.12: The joint posterior distribution, scatter plot of beta0 and beta1.

此圖98.12提示我們該邏輯回歸模型的截距(intercept)beta0，和斜率(slope)beta1其實是高度相關的。這導致了未知參數(兩個回歸系數)的事後概率分布樣本高度內部相關(high autocorrealtion within the samples of each individual parameter)。這是他們效率低下，需要大量的採集樣本仍然無法滿足或者達到理想的收斂的主要原因。

給邏輯回歸的回歸系數中心化之後的模型：我們來把兩個回歸系數的樣本中心化(centre the covariate \(x\))。在BUGS語言中可以使用x[i] - mean(x[])的命令來把未知參數的事後概率分布MCMC採樣過程中心化。然後我們重復一下上面的計算過程，看結果有怎樣的變化。與前者的分析比較一下收斂所需要的時間和未知參數事後估計的效率差別。

# logistic regression model with centred covariate
model{
  for(i in 1:N){# loop through experiments
              y[i] ~ dbin(theta[i], n[i])
   logit(theta[i]) <- beta0 + beta1 * (x[i] - mean(x[]))
  }
  # priors 
  beta0 ~ dunif(-100, 100)
  beta1 ~ dunif(-100, 100)
}

# JAGS codes:
# 
Dat <- list(
     y = c(1, 3, 6, 8, 11, 15, 17, 19), 
     n = c(20, 20, 20, 20, 20, 20, 20, 20), 
     x = c(30, 32, 34, 36, 38, 40, 42, 44), 
     N = 8 
)

# step 1 check model
jagsModel <- jags.model(
                     file = paste(bugpath, 
                                  "/backupfiles/logistic-reg-model-centred.txt",
                                  sep = ""),
                     data = Dat,
                     n.chains = 2, 
                     # inits = inits,
                     quiet = TRUE)
# Step 2 update 10000 iterations

update(jagsModel, n.iter = 1, progress.bar = "none")

# Step 3 set monitor variables

codaSamples <- coda.samples(
  jagsModel, variable.names = c("beta0", "beta1", "theta[6]"),
  n.iter = 10000, progress.bar = "none"
)

mcmcplots::traplot(codaSamples, c("beta0", "beta1", "theta[6]"))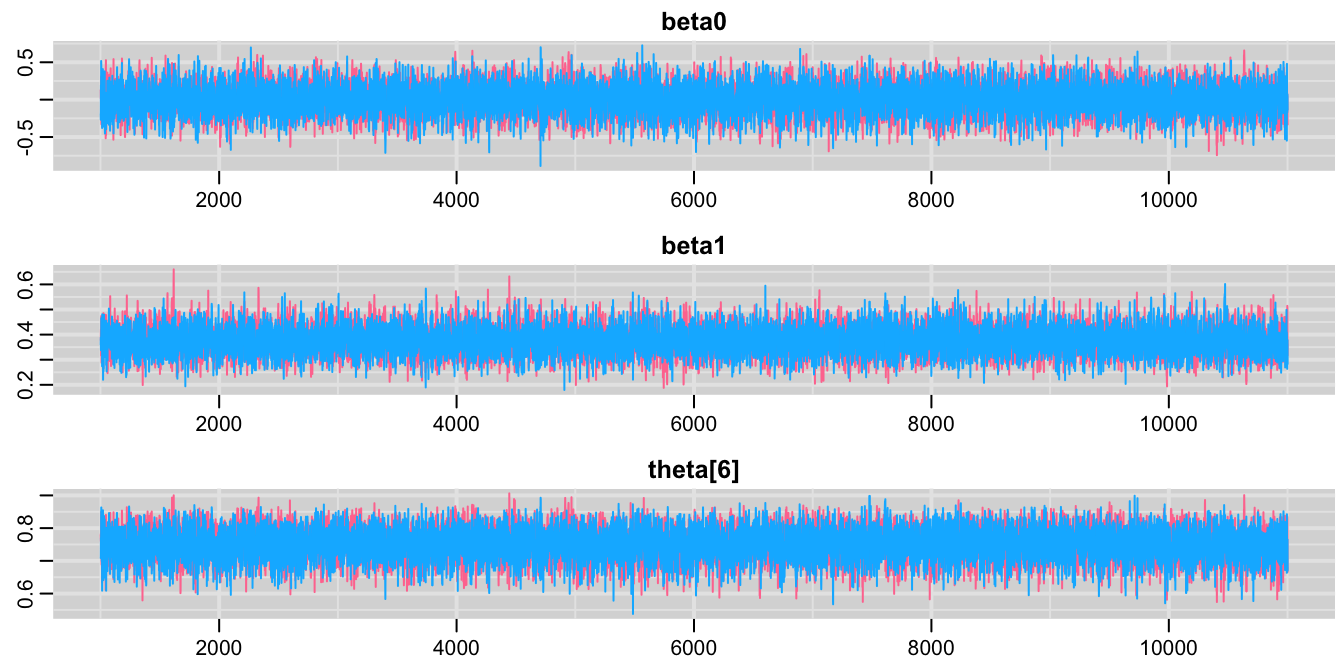

圖 98.13: History plots based on first 10000 iterations with centred covariates.

用中心化之後的模型我們發現需要10000或更多的起始樣本來達到事後概率分布的收斂。BGR診斷圖 98.14 也提示我們大概在10000次之後的重復採樣才能達到收斂。所以我們決定要刨除起始10000次採集的樣本。(burn-in = 10000)

gelman.diag(codaSamples)

## Potential scale reduction factors:
## 
##          Point est. Upper C.I.
## beta0             1          1
## beta1             1          1
## theta[6]          1          1
## 
## Multivariate psrf
## 
## 1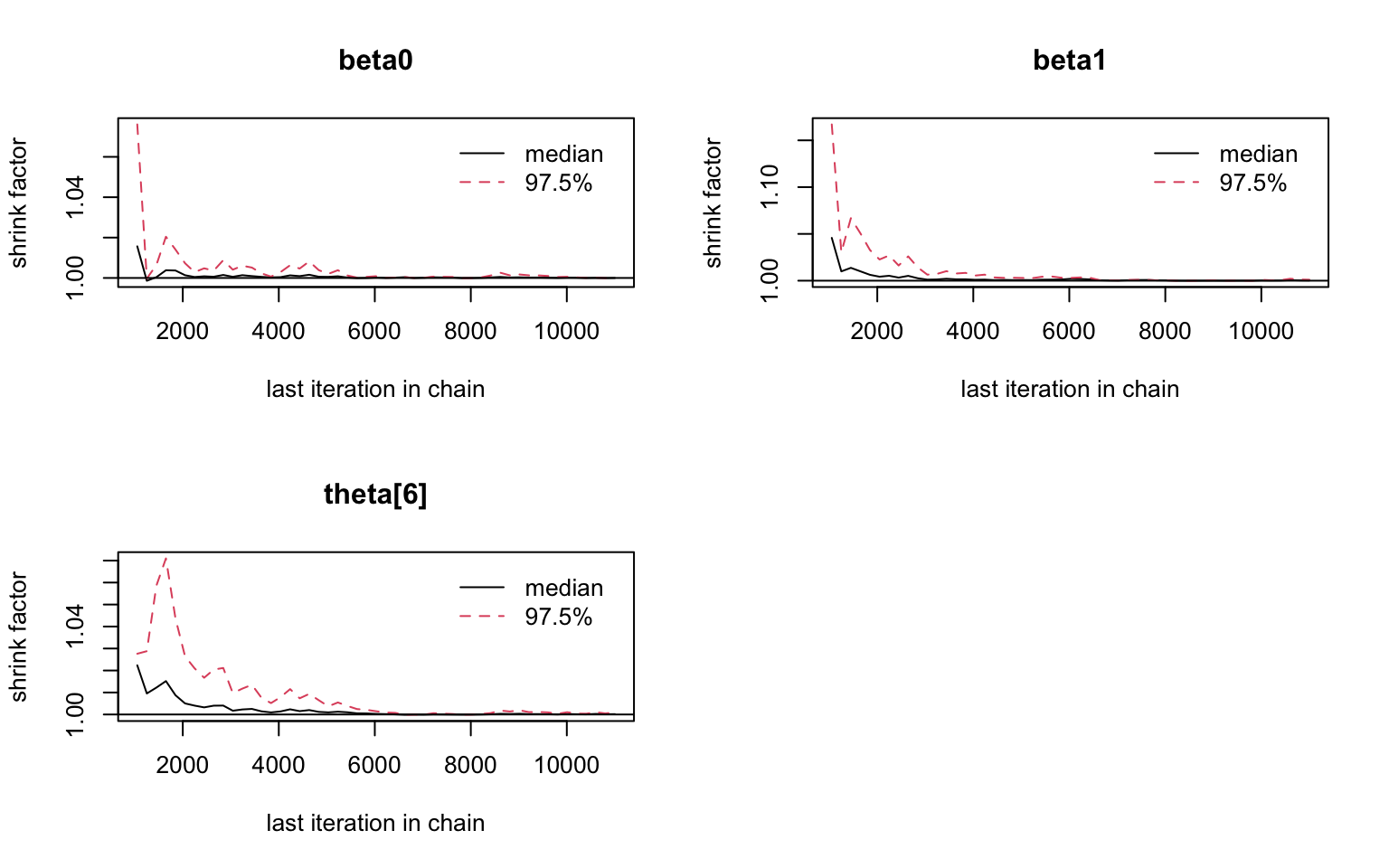

gelman.plot(codaSamples)

圖 98.14: Brooks-Gelman-Rubin diagnostic graph

刨除了起始10000次採集的樣本之後，剩餘的MCMC樣本的自相關也基本都降至0，說明這時候採集的事後概率分布樣本基本上都可以認爲是相互獨立的樣本。此時有效樣本量基本上約等於採集到的樣本量。

# R2JAGS codes
Dat <- list(
     y = c(1, 3, 6, 8, 11, 15, 17, 19), 
     n = c(20, 20, 20, 20, 20, 20, 20, 20), 
     x = c(30, 32, 34, 36, 38, 40, 42, 44), 
     N = 8 
)
post.jags <- jags(
  data = Dat,
  # inits = inits,
  parameters.to.save = c("beta0", "beta1", "theta[6]"),
  n.iter = 20000,
  model.file = paste(bugpath,
                     "/backupfiles/logistic-reg-model-centred.txt",
                     sep = ""),
  n.chains = 2,
  n.thin = 1,
  n.burnin = 10000,
  progress.bar = "none")

## Compiling model graph
##    Resolving undeclared variables
##    Allocating nodes
## Graph information:
##    Observed stochastic nodes: 8
##    Unobserved stochastic nodes: 2
##    Total graph size: 63
## 
## Initializing model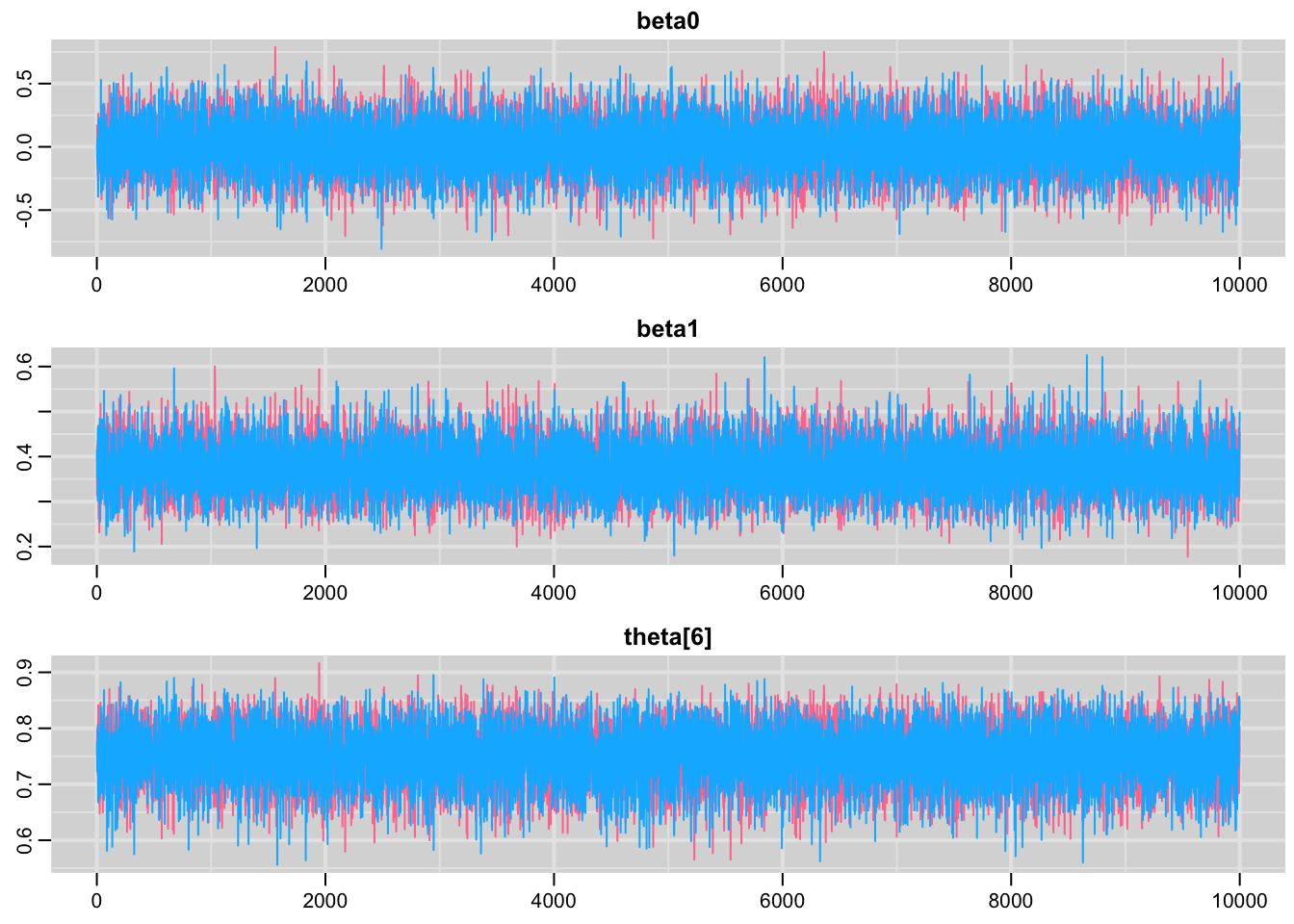

mcmcplots::traplot(post.jags, c("beta0", "beta1", "theta[6]"))

print(post.jags)

## Inference for Bugs model at "/Users/chaoimacmini/Downloads/LSHTMlearningnote/backupfiles/logistic-reg-model-centred.txt", fit using jags,
##  2 chains, each with 20000 iterations (first 10000 discarded)
##  n.sims = 20000 iterations saved
##          mu.vect sd.vect   2.5%    25%    50%    75%  97.5%  Rhat n.eff
## beta0     -0.002   0.206 -0.404 -0.143 -0.002  0.137  0.404 1.001 20000
## beta1      0.374   0.057  0.267  0.336  0.373  0.411  0.491 1.001  6800
## theta[6]   0.751   0.049  0.650  0.719  0.752  0.786  0.841 1.001  9100
## deviance  25.764   2.018 23.763 24.303 25.140 26.579 31.147 1.001  6500
## 
## For each parameter, n.eff is a crude measure of effective sample size,
## and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
## 
## DIC info (using the rule, pD = var(deviance)/2)
## pD = 2.0 and DIC = 27.8
## DIC is an estimate of expected predictive error (lower deviance is better).

Simulated <- coda::as.mcmc(post.jags)
ggSample <- ggs(Simulated)

ggSample %>% 
  filter(Iteration >= 2001 & Parameter %in% c("beta0", "beta1")) %>% 
  ggs_autocorrelation()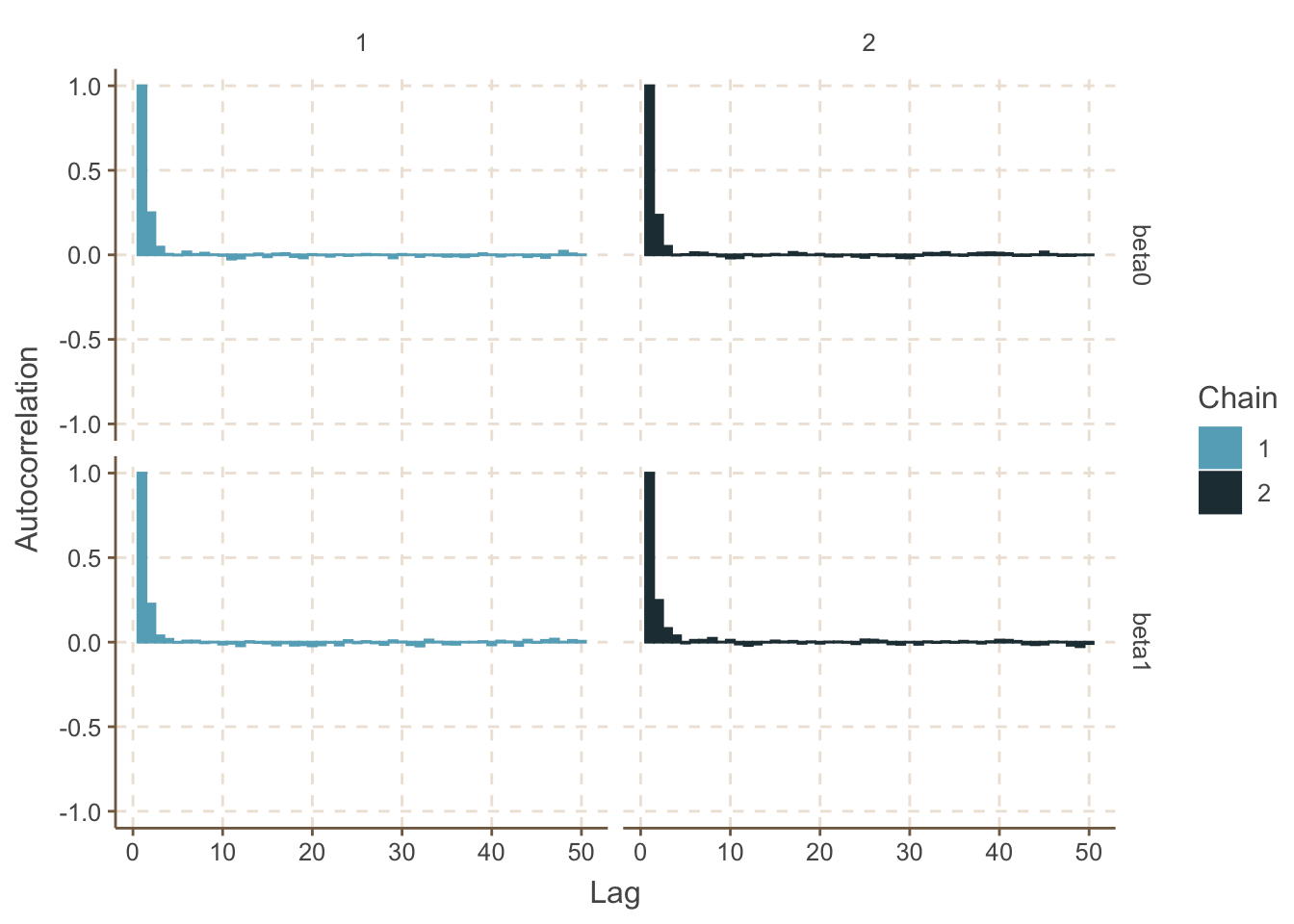

這時候我們獲得的回歸系數的事後估計的均值 beta1 = 0.377，和它的95%可信區間，0.271, 0.492。它其實是藥物劑量每增加1mg，隨之增加的藥物有效百分比的對數比值比 (log-odds-ratio of a positive response per 1 mg increase in dose.)，你有沒有發現其實我們很難解釋這個變量的實際含義呢？有沒有什麼辦法可以來改善這個結果，讓它更加容易讓人明白呢？
想辦法在未知參數被中心的話邏輯回歸模型中增加新的語句，生成一些新的容易讓人解釋的變量，改善模型的易解釋程度。也許你可以把對數比值比轉換成比值比，你也許可以自己算一下在哪種劑量條件下可以讓95%的患者都有治療療效(ED95)：

\[ \begin{aligned} \text{logit}0.95 & = \beta_0 + \beta_1(ED95 - \bar x) \\ \Rightarrow ED95 & = (\text{logit}0.95 - \beta_0)/\beta_1 + \bar x \end{aligned} \]

# logistic regression model with centred covariate 
# and added statements
model{
  for(i in 1:N){# loop through experiments
              y[i] ~ dbin(theta[i], n[i])
   logit(theta[i]) <- beta0 + beta1 * (x[i] - mean(x[]))
  }
  # priors 
  beta0 ~ dunif(-100, 100)
  beta1 ~ dunif(-100, 100)
  
  # generated values
  OR <- exp(beta1) # odds ratio of positive response per 1 mg increase in dose
  ED95 <- (logit(0.95) - beta0)/beta1 + mean(x[]) # dose that gives 95% of maximal response
  logit(P35) <- beta0 + beta1 * (35 - mean(x[])) # probability of positive reaction if given 35mg drugs
}

# R2JAGS codes:
Dat <- list(
     y = c(1, 3, 6, 8, 11, 15, 17, 19), 
     n = c(20, 20, 20, 20, 20, 20, 20, 20), 
     x = c(30, 32, 34, 36, 38, 40, 42, 44), 
     N = 8 
)

post.jags <- jags(
  data = Dat,
  # inits = inits,
  parameters.to.save = c("ED95", "OR", "P35", "beta0", "beta1"),
  n.iter = 20000,
  model.file = paste(bugpath,
                     "/backupfiles/logistic-reg-model-centred-stat.txt",
                     sep = ""),
  n.chains = 2,
  n.thin = 1,
  n.burnin = 10000,
  progress.bar = "none")

## Compiling model graph
##    Resolving undeclared variables
##    Allocating nodes
## Graph information:
##    Observed stochastic nodes: 8
##    Unobserved stochastic nodes: 2
##    Total graph size: 76
## 
## Initializing model

# mcmcplots::traplot(post.jags, c("beta0", "beta1", "theta[6]"))
print(post.jags)

## Inference for Bugs model at "/Users/chaoimacmini/Downloads/LSHTMlearningnote/backupfiles/logistic-reg-model-centred-stat.txt", fit using jags,
##  2 chains, each with 20000 iterations (first 10000 discarded)
##  n.sims = 20000 iterations saved
##          mu.vect sd.vect   2.5%    25%    50%    75%  97.5%  Rhat n.eff
## ED95      45.045   1.384 42.746 44.083 44.887 45.860 48.148 1.001 20000
## OR         1.457   0.082  1.310  1.399  1.451  1.510  1.633 1.001 15000
## P35        0.323   0.050  0.227  0.288  0.322  0.356  0.423 1.001 20000
## beta0     -0.001   0.205 -0.405 -0.140  0.001  0.138  0.400 1.001 20000
## beta1      0.375   0.056  0.270  0.336  0.373  0.412  0.491 1.001 20000
## deviance  25.741   2.038 23.758 24.297 25.122 26.516 31.170 1.001 20000
## 
## For each parameter, n.eff is a crude measure of effective sample size,
## and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
## 
## DIC info (using the rule, pD = var(deviance)/2)
## pD = 2.1 and DIC = 27.8
## DIC is an estimate of expected predictive error (lower deviance is better).

所以，藥物每增加劑量1mg，有療效的比值比是OR = 1.46 (95%CrI: 1.31, 1.63)。能夠達到95%患者都有療效的劑量是 45.02 mg (95% CrI: 42.7, 48.2 mg)。如果給予患者藥物劑量爲 35 mg，患者的疼痛能夠得到緩解(有療效)的概率是 32.3% (95% CrI: 22.7%, 42.3%)。跟着看到這裏的你是不是也覺得貝葉斯的結果和過程能夠更加豐富地回答我們想知道的問題呢？

#### PLOT THE DENSITY and HISTOGRAMS OF THE SAMPLED VALUES
par(mfrow=c(3,1))
Simulated <- coda::as.mcmc(post.jags)
ggSample <- ggs(Simulated)

ED95 <- ggSample %>% 
  filter(Parameter == "ED95")
OR <- ggSample %>% 
  filter(Parameter == "OR")
P35 <- ggSample %>% 
  filter(Parameter == "P35")

plot(density(ED95$value), main = "ED95 sample", 
     ylab = "P(ED95)", xlab = "Distribution of ED95", col = "red")
plot(density(OR$value), main = "OR sample", 
     ylab = "P(OR)", xlab = "Distribution of OR", col = "red")
plot(density(P35$value), main = "P35 sample", 
     ylab = "P(P35)", xlab = "Distribution of P35", col = "red")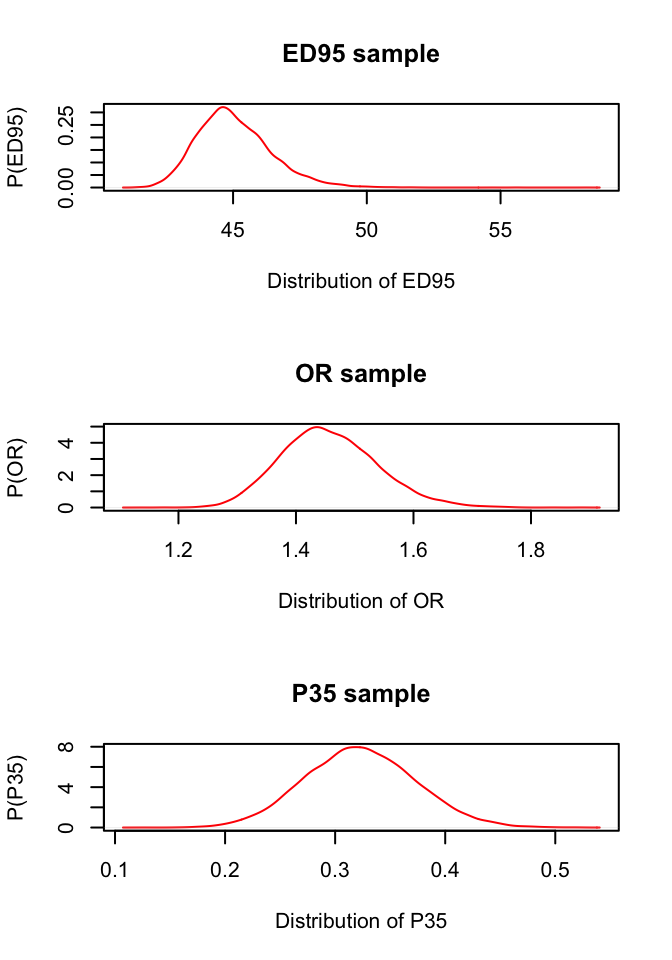

圖 98.15: Posterior density plots of ED95, OR, and P35.

References

Raftery, Adrian E., and Steven Lewis. 1992. “How Many Iterations in the Gibbs Sampler?” In In Bayesian Statistics 4, 763–73. Oxford University Press.

第 98 章 馬爾可夫鏈蒙特卡羅MCMC，圖形模型，BUGS語言