第 103 章 再訪 MCMC
和我們之前在介紹MCMC(Markov Chain Monte Carlo)時 (Chapter 98)介紹過的那樣,大部分的統計模型其事後概率分佈的直接樣本 \(p(\theta|x)\) 採集是十分困難的。但是我們可以使用間接的算法實施採樣過程。吉布斯樣本採集 (Chapter 98.1.2) 是美特羅波利斯-海斯廷斯(Metroplis-Hastings)算法(algorithm)的特殊形態。本章我們來深入探討Metropolis-Hastings算法具體的實施過程是怎樣進行的。
103.1 Metropolis-Hastings algorithm
美特羅波利斯-海斯廷斯算法在歷史上爲統計學打開了一扇嶄新的大門。因爲它的發明,我們現在可以繞過複雜的微積分計算過程,對幾乎任何一種分佈實施樣本採集。這一種要算法的發明,不僅僅對於貝葉斯統計學來說是一個重大突破,同時也爲傳統的概率論統計學提供了強有力的算法。
具體的算法過程較爲複雜,我們可以不用完全掌握其所有細節,但是我們應該明白它的大致採集樣本的原理。理解了它的採樣原理,有助於我們實際操作時選取合適的參數(parameters),從目標分佈中獲取品質優良的隨機樣本。它的基本原理框架是這樣的:
- 先從變量可能的取值樣本中,爲\(X_0\)選取一個起始值 (starting value),我們稱之爲”現在值 current” \((X_{t-1} = X_0)\);
- 以第一步選取的預測變量現在值爲條件 \(g(Y|X_{t-1})\),隨機設定一個候選變量(candidate \(Y_t\))的分佈,例如可以是典型的高斯(正態)分佈:\(Y_t \sim N(X_{t-1}, \sigma)\);
- 隨機從第二步設定的分佈中選取 \(Y_t\) 作爲樣本 \((X_t)\) 的第二個元素,同時滿足下面的概率關係: \[ P(X_t = Y_t) = min(1, \frac{P(Y_t|data)/g(Y_t|X_{t-1})}{P(X_{t-1}|data)/g(X_{t-1}|Y_t)}) \]
- 假設你沒有選擇 \(Y_t\) 那麼 \(X_{t-1}\) 會被重複選取作爲樣本的元素,\(X_t = X_{t-1}\);
- 回到第二步,然後進行下一個樣本(increase \(t\) by 1)的採集。
在上面的公式中, \(P(Y_t|data)\)是利用指定(的先驗概率)分佈的概率密度方程(probability density function, pdf)中隨機選取的 \(Y_t\) 計算獲得的概率。這個方程包含了一個很大概率我們人類無法計算的積分分母:\(\int P(data|\theta)P(\theta)\)。(however, the method also works if we substitute any function proportional to the posterior because the proportionality constant will cancel out)但是在計算過程中如果我們用與該事後概率密度分佈成比例的方程將之替代掉,那麼這部分複雜的積分方程會由於成比例性最終同時在分子分母中被抹去。例如常用的是事後概率分佈密度方程的分子部分: \(f(Y_t) = P(data|Y_t)\times P(Y_t) \propto P(Y_t|data)\)。另外,如果用於採集樣本的分佈 \(g\) 是左右對稱的:\(g(Y_t|X_{t-1}) = g(X_{t-1}|Y_t)\),算法會簡化成爲 Metropolis 算法:
\[ P(X_t = Y_t) = min(1, \frac{f(Y_t)}{f(X_{t-1})}) \]
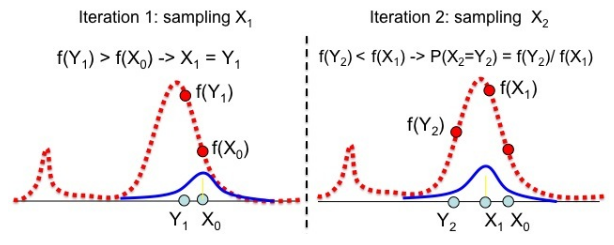
圖 103.1: Sampling with the Metropolis-Hastings algorithm