第 59 章 二項分佈數據的廣義線性迴歸模型 logistic regression model
二項分佈數據在醫學研究中很常見,例子有千千萬,下面這些只是作爲拋磚引玉:
- 心臟搭橋手術和血管成形術兩組病人比較療效時,結果變量可以是:死亡 (是/否);心肌梗死發作 (是/否);
- 機械心臟瓣膜手術結果:成功/失敗;
- 用小鼠作不同劑量二硫化碳暴露下的毒理學實驗,結果變量是:小鼠死亡 (是/否);
- 隊列研究中追蹤對象中出現心肌梗死病例,結果變量是:心肌梗死發作 (是/否)。
59.1 彙總後/個人 (grouped / individual) 的二項分佈數據
下面的數據,來自某個毒理學實驗,不同劑量的二硫化碳暴露下小鼠的死亡數和總數的數據:
## dose n_deaths n_subjects
## 1 49.06 6 59
## 2 52.99 13 60
## 3 56.91 18 62
## 4 60.84 28 56
## 5 64.76 52 63
## 6 68.69 53 59
## 7 72.61 60 62
## 8 76.54 59 60很容易理解這是一個典型的彙總後二項分佈數據 (grouped binary data)。每組不同的劑量,第二列,第三列分別是死亡數和實驗總數。另外一種個人二項分佈數據 (individual binary data) 的形式是這樣的:
## dose death
## 1 49.06 1
## 2 49.06 1
## 3 49.06 1
## 4 49.06 1
## 5 49.06 1
## 6 49.06 1
## 7 49.06 0
## 8 49.06 0
## 9 49.06 0
## 10 49.06 0
## 11 . .
## 12 . .
## 13 . .個人二項分佈數據其實就是把每個觀察對象的事件發生與否的信息都呈現出來。通常個人二項分佈數據又被稱爲伯努利數據,分組型的二項分佈數據被稱爲二項數據。兩種表達形式,但是存儲的是一樣的數據。
59.2 二項分佈數據的廣義線性迴歸模型
而所有的 GLM 一樣,二項分佈的 GLM 包括三個部分:
- 因變量的分佈 Distribution:因變量應相互獨立,且服從二項分佈
\[\begin{aligned} Y_i &\sim \text{Bin}(n_i, \pi_i), i = 1, \cdots, n \\ E(Y_i) &= \mu_i = n_i\pi_i\end{aligned}\] - 線性預測方程 Linear predictor:第 \(i\) 名觀測對象的預測變量的線性迴歸模型
\[\eta_i = \alpha + \beta_1 x_{i1} + \cdots + \beta_p x_{ip}\] - 鏈接方程 Link function:鏈接方程連接的是 \(\mu_i = n\pi_i\) 和線性預測方程。一個二項分佈因變量數據,可以有許多種鏈接方程:
- \(\mathbf{logit}:\) \[\text{logit}(\pi) = \text{ln}(\frac{\pi}{1-\pi})\]
- \(\mathbf{probit}:\) \[\text{probit}(\pi) = \Phi^{-1}(\pi)\]
- \(\mathbf{complementary\; log-log}:\) \[\text{cloglog}(\pi) = \text{ln}\{ - \text{ln}(1-\pi) \}\]
- \(\mathbf{log:}\) \[\text{log}(\pi) = \text{ln}(\pi)\]
59.3 注
- 概率鏈接方程 \(\text{probit}\),\(\Phi\) 被定義爲標準正態分佈的累積概率方程 (Section 7.3): \[\Phi(z) = \text{Pr}(Z \leqslant z), \text{ for } Z\sim N(0,1)\]
- 二項分佈數據的標準參數 (canonical parameter) \(\theta_i\) 的標準鏈接方程是 \(\theta_i = \text{logit}(\pi_i)\)。
- \(\text{logit, probit, complementary log-log}\) 三種鏈接方程都能達到把閾值僅限於 \(0 \sim 1\) 之間的因變量概率映射到線性預測方程的全實數閾值 \((-\infty,+\infty)\) 的目的。但是最後一個 \(\text{log}\) 鏈接方程只能映射全部的非零負實數 \((-\infty,0)\)。
- \(\text{logit, probit}\) 鏈接方程都是以 \(\pi= 0.5\) 爲對稱軸左右對稱的。但是 \(\text{cloglog}\) 則沒有對稱的性質。
- 鏈接方程 \(\text{log}\) 具有可以直接被解讀爲對數危險度比 (log Risk Ratio) 的優點,所以也常常在應用中見到。對數鏈接方程還有其他的優點 (非塌陷性 non-collapsibility),但是它的最大缺點是,有時候利用這個鏈接方程的模型無法收斂 (converge)。
- \(\text{logit}\) 鏈接方程是我們最常見的,也最直觀易於理解。利用這個鏈接方程擬合的模型的迴歸係數能夠直接被理解爲對數比值比 (log Odds Ratio)。
- 如果是個人數據 (individual data),那麼 \(n_i = 1\),\(i\) 是每一個觀測對象的編碼。那麼 \(Y_i = 0\text{ or }1\),代表事件發生或沒發生/成功或者失敗。如果是分組數據 (grouped data),\(i\) 是每個組的編號,\(n_i\) 指的是第 \(i\) 組中觀測對象的人數,\(Y_i\) 是第 \(i\) 組的 \(n\) 名對象中事件發生的次數/成功的次數。
59.3.1 Exercise. Link functions.
推導出鏈接參數分別是
- \(\text{log}\)
- \(\text{logit}\)
- \(\text{complementary log-log}\)
時,用參數 \(\alpha, \beta_1, \cdots, \beta_p\) 表達的參數 \(\pi_i=?, E(Y_i)=\mu_i=?\)
解
\(\text{log}\) \[ \begin{aligned} \text{ln}(\pi_i) & = \alpha + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip} \\ \Rightarrow \pi_i & = e^{\alpha + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip}} \\ \mu_i & = n_i\pi_i = n_i e^{\alpha + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip}} \end{aligned} \]
\(\text{logit}\)
\[ \begin{aligned} \text{logit}(\pi_i) & = \text{ln}(\frac{\pi_i}{1-\pi_i}) \\ & = \alpha + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip} \\ \Rightarrow \pi_i & = \frac{e^{\alpha + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip}}}{1+e^{\alpha + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip}}} \\ \mu_i & = \frac{n_i e^{\alpha + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip}}}{1+e^{\alpha + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip}}} \end{aligned} \]
- \(\text{complementary log-log}\)
\[ \begin{aligned} \text{cloglog}(\pi_i) & = \text{ln}\{ - \text{ln}(1-\pi) \} \\ & = \alpha + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip} \\ \Rightarrow \pi_i & = 1 - e^{-e^{\alpha + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip}}} \\ \mu_i & = n_i\pi_i = n_i(1-e^{-e^{\alpha + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip}}}) \end{aligned} \]
59.4 邏輯迴歸模型迴歸係數的實際意義
邏輯迴歸 (logistic regression) 的模型可以寫成是
\[ \text{logist}(\pi_i) = \text{ln}(\frac{\pi_i}{1-\pi_i}) = \alpha + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip} \]
假如觀察對象 \(j\) 和 \(i\) 兩人中,其餘的預測變量都相同,二者之間有且僅有最後一個預測變量相差一個單位:
\[ \begin{aligned} \text{logit}(\pi_j) & = \text{ln}(\frac{\pi_j}{1-\pi_j}) = \alpha + \beta_1 x_{j1} + \beta_2 x_{j2} + \cdots + \beta_p x_{jp} \\ \text{logit}(\pi_i) & = \text{ln}(\frac{\pi_i}{1-\pi_i}) = \alpha + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip} \\ \text{Because they are} & \text{ in the same model share the same parameters, and } \\ x_{jp} & = x_{ip} + 1\\ \Rightarrow \text{logit}(\pi_j) - \text{logit}(\pi_i) & = \beta_p (x_{jp} + 1 - x_{jp}) = \beta_p \\ \Rightarrow \beta_p & = \text{ln}(\frac{\pi_j}{1-\pi_j}) - \text{ln}(\frac{\pi_i}{1-\pi_i}) \\ & = \text{ln}(\frac{\frac{\pi_j}{1-\pi_j}}{\frac{\pi_i}{1-\pi_i}}) \\ & = \text{ln}(\text{Odds Ratio}) \end{aligned} \]
所以迴歸係數 \(\beta_p\) 可以被理解爲是 \(j\) 與 \(i\) 相比較時的對數比值比 log Odds Ratio。我們只要對迴歸係數求反函數,即可求得比值比。
59.5 邏輯迴歸實際案例
一組數據如下:
其中,牲畜來自兩大羣 (group);每羣有五個組的牲畜被飼養五種不同濃度的飼料 (dfactor);每組牲畜我們記錄了牲畜的總數 (cattle) 以及感染了瘋牛病的牲畜數量 (infect):
## group dfactor cattle infect
## 1 1 1 11 8
## 2 1 2 10 7
## 3 1 3 12 5
## 4 1 4 11 3
## 5 1 5 12 2
## 6 2 1 10 10
## 7 2 2 10 9
## 8 2 3 12 8
## 9 2 4 11 6
## 10 2 5 10 459.5.2 模型 1 飼料 + 羣
\[ \begin{aligned} \text{Assume } Y_i & \sim \text{Bin} (n_i, \pi_i) \\ \text{logit}(\pi_i) & = \alpha + \beta_1 x_{i1} + \beta_2 x_{i2} \end{aligned} \]
Model1 <- glm(cbind(infect, cattle - infect) ~ factor(group) + dfactor, family = binomial(link = logit), data = Cattle)
summary(Model1)##
## Call:
## glm(formula = cbind(infect, cattle - infect) ~ factor(group) +
## dfactor, family = binomial(link = logit), data = Cattle)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.60847 -0.17831 0.10110 0.31150 1.16876
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 2.13104 0.61130 3.4861 0.0004902 ***
## factor(group)2 1.30590 0.46540 2.8060 0.0050163 **
## dfactor -0.78744 0.18135 -4.3422 0.00001411 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 33.52556 on 9 degrees of freedom
## Residual deviance: 2.45082 on 7 degrees of freedom
## AIC: 32.2537
##
## Number of Fisher Scoring iterations: 4##
## OR lower95ci upper95ci Pr(>|Z|)
## factor(group)2 3.69102114 1.48251011 9.18957451 0.005016342395
## dfactor 0.45500721 0.31889988 0.64920551 0.000014109282於是,我們可以寫下這個邏輯迴歸的數學模型:
\[ \begin{aligned} \text{logit}(\hat\pi_i) & = \text{ln}(\frac{\hat\pi_i}{1-\hat\pi_i}) = \hat\alpha + \hat\beta_1 x_{i1} + \hat\beta_2 x_{i2} \\ & = 2.1310 - 0.7874 \times \text{dfactor} + 1.3059 \times \text{group} \end{aligned} \]
解讀這些參數估計的意義
- 截距 \(\hat\alpha = 2.1310\) 的含義是,當 \(x_{1}, x_{2}\) 都等於零,i.e. 飼料濃度 0,在第一羣的那些牲畜感染瘋牛病的對數比值 (log-odds);
- 斜率 \(\hat\beta_1 = -0.7874\) 的含義是,當牲畜羣不變時,飼料濃度每增加一個單位,牲畜感染瘋牛病的對數比值的估計變化量 (estimated increase in log odds of infection);
- 迴歸係數 \(\hat\beta_2 = 1.3059\) 的含義是,當飼料濃度不變時,兩羣牲畜之間感染瘋牛病的對數比值比 (log-Odds Ratio),所以第二羣牲畜比第一羣牲畜感染瘋牛病的比值比的估計量,以及 \(95\%\text{CI}\) 的計算方法就是:
\[\begin{aligned} \text{exp}(\hat\beta_2) & = \text{exp}(1.3059) = 3.69,\\ \text{ with 95% CI: } & \text{exp}(\hat\beta_2 \pm 1.96\times \text{Std.Error}_{\hat\beta_2}) \\ & = (1.48, 9.19) \end{aligned}\]
59.5.3 模型 2 增加交互作用項 飼料 \(\times\) 羣
飼料濃度與瘋牛病感染之間的關係,是否因爲牲畜所在的 “羣” 不同而發生改變?
定義增加了飼料和羣交互作用項的邏輯迴歸模型:
\[ \text{logit}(\pi_i) = \alpha + \beta_1 x_{i1} + \beta_2 x_{i2} + \beta_3 x_{i1}\times x_{i2} \]
Model2 <- glm(cbind(infect, cattle - infect) ~ factor(group) + dfactor + factor(group)*dfactor, family = binomial(link = logit), data = Cattle)
summary(Model2)##
## Call:
## glm(formula = cbind(infect, cattle - infect) ~ factor(group) +
## dfactor + factor(group) * dfactor, family = binomial(link = logit),
## data = Cattle)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.71914 -0.16508 -0.02111 0.34451 1.00127
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.89028 0.73584 2.5689 0.010203 *
## factor(group)2 1.98867 1.34471 1.4789 0.139172
## dfactor -0.70508 0.22955 -3.0716 0.002129 **
## factor(group)2:dfactor -0.20583 0.37553 -0.5481 0.583619
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 33.52556 on 9 degrees of freedom
## Residual deviance: 2.14476 on 6 degrees of freedom
## AIC: 33.9477
##
## Number of Fisher Scoring iterations: 4##
## OR lower95ci upper95ci Pr(>|Z|)
## factor(group)2 7.30580425 0.52365757 101.92686809 0.1391720038
## dfactor 0.49406759 0.31506152 0.77477816 0.0021289774
## factor(group)2:dfactor 0.81396890 0.38989883 1.69927508 0.5836187644從輸出的報告來看,增加了交互作用項以後,在第一羣牲畜中,飼料濃度每增加一個單位,感染瘋牛病的比值比 (OR) 是
\[ \text{exp}(-0.7051) = 0.49 \]
在第二羣牲畜中,飼料濃度每增加一個單位,感染瘋牛病的比值比 (OR) 變成了
\[ \text{exp}(-0.7051 - 0.2058) = 0.40 \]
通過對 \(\hat\beta_3 = 0\) 的假設檢驗,就可以推斷飼料濃度和感染瘋牛病之間的關係是否因爲不同牲畜 “羣” 而不同。所以上面的報告中也已經有了交互作用項的檢驗結果 \(p = 0.584\),所以,此處可以下的結論是:沒有足夠的證據證明交互作用存在。
59.6 GLM-Practical 03
數據來自一個毒理學實驗,該實驗中 8 組昆蟲在不同濃度的二硫化碳下暴露四個小時,實驗的目的是研究二硫化碳劑量和昆蟲死亡率之間的關系。
59.6.1 昆蟲的死亡率
Insect <- read.table("../backupfiles/INSECT.RAW", header = FALSE, sep ="", col.names = c("dose", "n_deaths", "n_subjects"))
print(Insect)## dose n_deaths n_subjects
## 1 49.06 6 59
## 2 52.99 13 60
## 3 56.91 18 62
## 4 60.84 28 56
## 5 64.76 52 63
## 6 68.69 53 59
## 7 72.61 60 62
## 8 76.54 59 60- 計算每組實驗濃度下死亡昆蟲的比例
## dose n_deaths n_subjects p
## 1 49.06 6 59 0.10169492
## 2 52.99 13 60 0.21666667
## 3 56.91 18 62 0.29032258
## 4 60.84 28 56 0.50000000
## 5 64.76 52 63 0.82539683
## 6 68.69 53 59 0.89830508
## 7 72.61 60 62 0.96774194
## 8 76.54 59 60 0.98333333- 將濃度和死亡比例做散點圖
ggplot(Insect, aes(x = dose, y = p)) +
geom_point()+
scale_x_continuous(breaks = seq(50, 75, by = 5)) +
scale_y_continuous(breaks = seq(0, 1, by = 0.2)) +
theme(axis.text = element_text(size = 15),
axis.text.x = element_text(size = 15),
axis.text.y = element_text(size = 15)) +
labs(x = "CS2 dose (mg/L)", y = "Proportion killed") +
theme(axis.title = element_text(size = 17), axis.text = element_text(size = 8),
axis.line = element_line(colour = "black"),
panel.border = element_blank(),
panel.background = element_blank())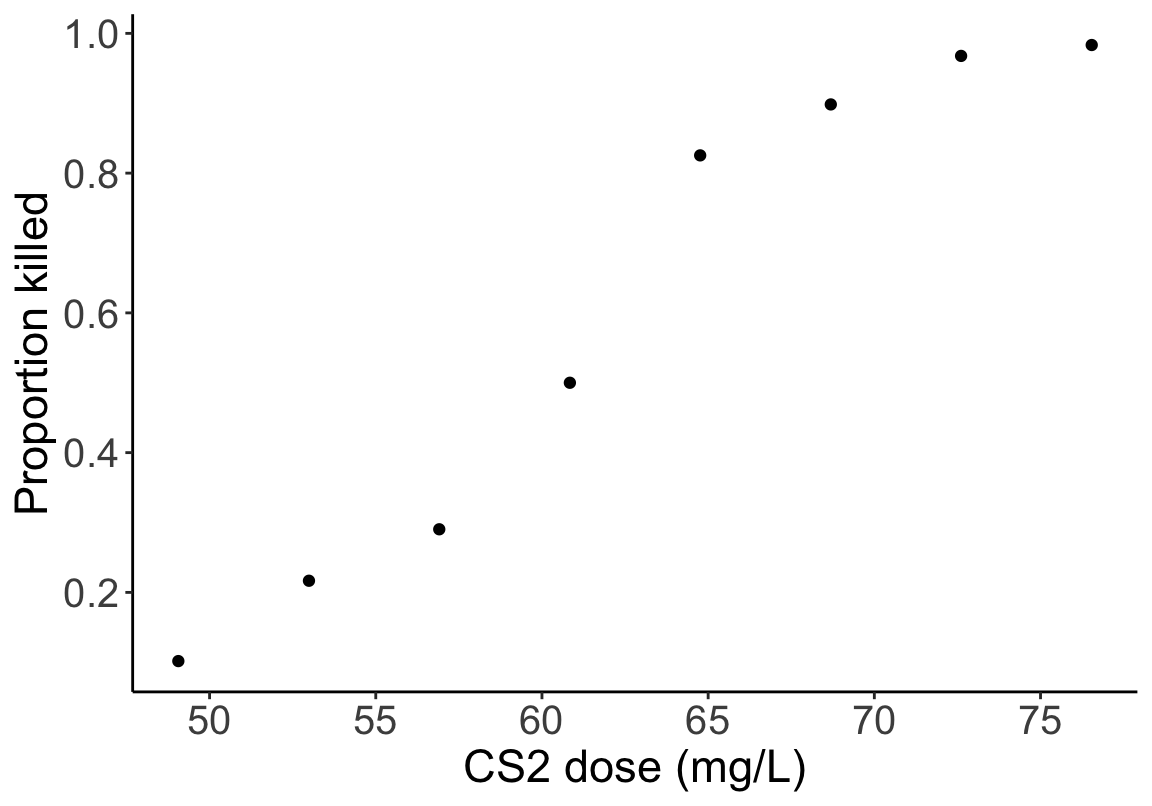
圖 59.1: Scatter plot of CS2 dose and proportion killed.
這裏如果使用線性回歸模型是不合適的,這是因爲:
- 散點圖提示濃度和死亡比例之間不是線性關系;
- “比例”這一數據被局限在 (0,1) 範圍之內,線性回歸的結果變量不會滿足這個條件;
- 觀察數據本身的方差不齊,也就是每個觀察點(死亡比例)的變化程度無法保證是相同的。
- 計算死亡比例的對數比值比 (log-odds),再作相同的散點圖,你會得出什麼樣的結論?
Insect <- Insect %>%
mutate(log_odds = log(p / (1-p)))
ggplot(Insect, aes(x = dose, y = log_odds)) +
geom_point()+
scale_x_continuous(breaks = seq(50, 75, by = 5)) +
scale_y_continuous(breaks = seq(-2, 4, by = 1)) +
theme(axis.text = element_text(size = 15),
axis.text.x = element_text(size = 15),
axis.text.y = element_text(size = 15)) +
labs(x = "CS2 dose (mg/L)", y = "Log odds of proportion killed") +
theme(axis.title = element_text(size = 17), axis.text = element_text(size = 8),
axis.line = element_line(colour = "black"),
panel.border = element_blank(),
panel.background = element_blank())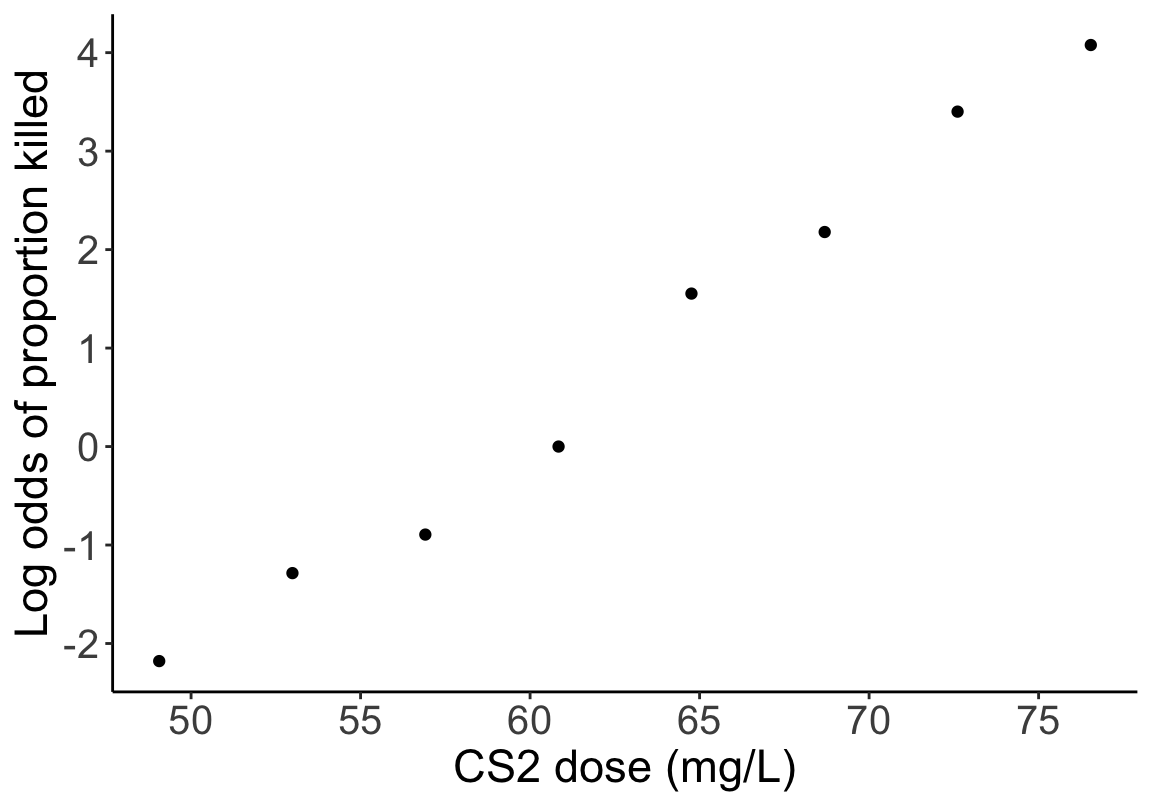
圖 59.2: Scatter plot of CS2 dose and log-odds of proportion killed.
死亡比例的對數比值比和二硫化碳濃度之間更加接近線性關系。
- 寫下此模型的數學表達式,你的表達式必須指明數據的分布,線性預測方程,和鏈接方程三個部分。用 R 擬合你寫下的模型。
解
本數據中,隨機變量是每組昆蟲中死亡的個數。用 \(Y_i\) 標記第 \(i\) 組昆蟲中死亡昆蟲數量,\(d_i\) 表示第 \(i\) 組昆蟲被暴露的二硫化碳濃度。對於所有的廣義線性回歸模型來說,它都由三個部分組成: 1) 反應量分布 the response distribution; 2) 鏈接方程 link function; 3) 線性預測方程 linear predictor.
反應量分布:
\[ Y_i \sim \text{Bin}(n_i, \pi_i),i = 1, \cdots, 8 \]
\(Y_i\) 的期望值是 \(\mu_i\) 的話,鏈接方程是
\[ \eta_i = \log(\frac{\mu_i}{n_i - \mu_i}) = \log(\frac{\pi_i}{1- \pi_i}) = \text{logit}(\pi_i) \]
線性預測方程是
\[ \eta_i = \beta_0 + \beta_1 d_i \]
用 R 來擬合這個模型:
Model1 <- glm(cbind(n_deaths, n_subjects - n_deaths) ~ dose, family = binomial(link = logit), data = Insect)
summary(Model1)##
## Call:
## glm(formula = cbind(n_deaths, n_subjects - n_deaths) ~ dose,
## family = binomial(link = logit), data = Insect)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.14983 -0.22403 0.25301 0.70846 0.99107
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -14.086403 1.228393 -11.467 < 2.2e-16 ***
## dose 0.236593 0.020303 11.653 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 268.26829 on 7 degrees of freedom
## Residual deviance: 4.61548 on 6 degrees of freedom
## AIC: 37.394
##
## Number of Fisher Scoring iterations: 4- 計算 CS2 在 55mg/l 時該模型預測的昆蟲死亡概率是多少。
\[ \text{logit}(\hat\pi_i) = -14.09 + 0.2366\times55 \\ \Rightarrow \hat\pi_i = \frac{\exp(-14.09 + 0.2366\times55)}{1+\exp(-14.09 + 0.2366\times55)} = 0.254 \]
- 計算昆蟲死亡比例達到50%的CS2濃度(LD50)。
當死亡比例達到一半時, \(\hat\pi = 0.5 \Rightarrow \text{logit}(\hat\pi) = 0\)
\[ 0 = -14.09 + 0.2366 \times \text{LD50} \\ \Rightarrow \text{LD50} = 59.5 \text{mg/l} \]
- 有證據證明昆蟲的死亡率隨着 CS2 濃度的增加而升高嗎?
有極強的證據證明昆蟲死亡率隨着 CS2 濃度增加而升高 \((z = 11.65, P < 0.001, \text{Wald test})\)。
- 將參數轉換成比值比,並解釋其實際含義。
CS2 濃每增加 1 個單位 (1 mg/l),昆蟲死亡率的比值比是 \(\exp(0.2366) = 1.27\),95% 信賴區間下限: \(\exp(0.2366 - 1.96\times0.0203) = 1.22\),上限: \(\exp(0.2366 + 1.96\times0.0203) = 1.32\)。
下面是在 R 裏計算的 OR 及其對應的信賴區間:
##
## Logistic regression predicting cbind(n_deaths, n_subjects - n_deaths)
##
## OR(95%CI) P(Wald's test) P(LR-test)
## dose (cont. var.) 1.27 (1.22,1.32) < 0.001 < 0.001
##
## Log-likelihood = -16.697
## No. of observations = 8
## AIC value = 37.394- 提取模型中擬合值 fitted value
## 1 2 3 4 5 6 7 8
## 0.077332565 0.175181106 0.349349622 0.576375269 0.774754491 0.897077450 0.956586871 0.982405536# to calculate the counts of numbers of deaths in each group
Model1$fitted.values * Insect$n_subjects## 1 2 3 4 5 6 7 8
## 4.5626213 10.5108663 21.6596766 32.2770151 48.8095329 52.9275695 59.3083860 58.9443322- 把模型擬合的概率和觀測概率放在同一個散點圖中比較:
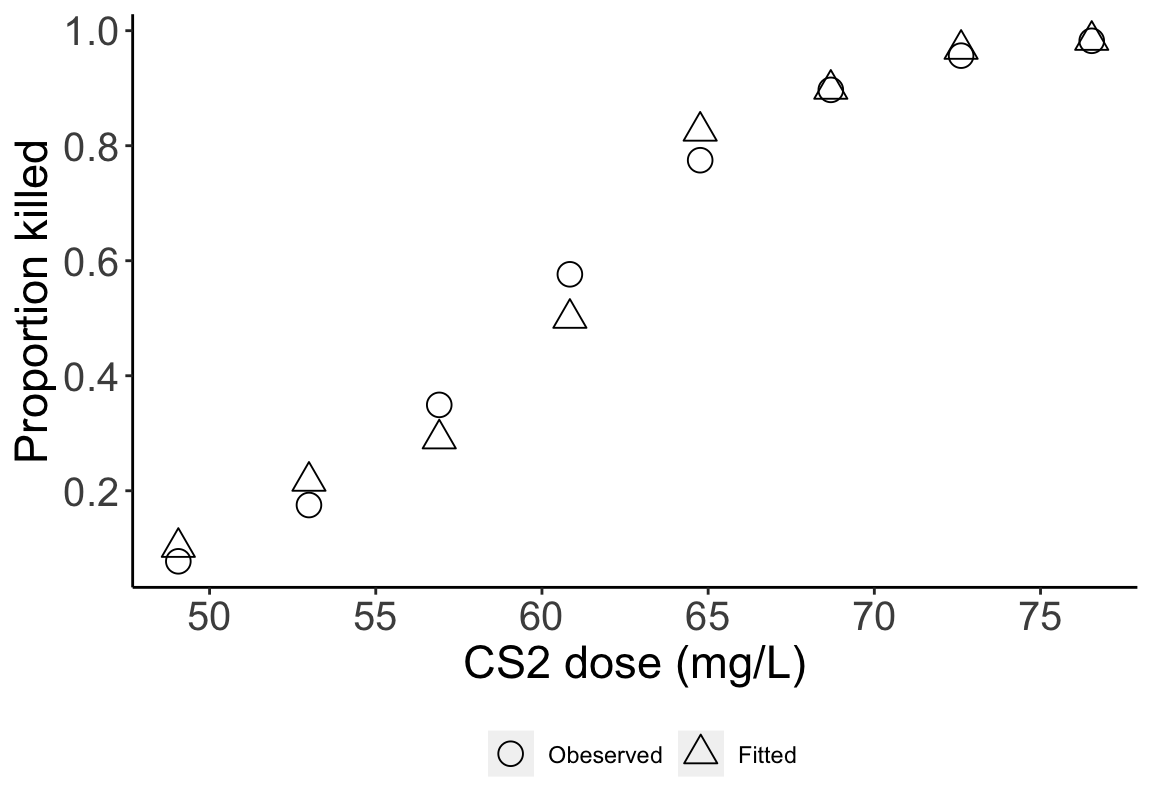
圖 59.3: Observed (circles) and fitted (triangles) proportions are generally similar, with differences greatest in the third and fourth dose groups.
- 現在計算一個新的濃度值 dose2 = dose2。這個新的變量用於分析是否模型中使用濃度平方可以提升模型的擬合優度。1) 用 Wald 檢驗的結果說明濃度平方的回歸系數是否有意義。2) 新模型的擬合值是否有所改善?
Insect <- Insect %>%
mutate(dose2 = dose^2)
Model2 <- glm(cbind(n_deaths, n_subjects - n_deaths) ~ dose + dose2, family = binomial(link = logit), data = Insect)
summary(Model2)##
## Call:
## glm(formula = cbind(n_deaths, n_subjects - n_deaths) ~ dose +
## dose2, family = binomial(link = logit), data = Insect)
##
## Deviance Residuals:
## 1 2 3 4 5 6 7 8
## -0.004545 0.634377 -0.691056 -0.681962 1.223967 -0.154036 -0.029880 -0.561968
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -2.4881722 9.8677198 -0.2522 0.8009
## dose -0.1500054 0.3291786 -0.4557 0.6486
## dose2 0.0031871 0.0027273 1.1686 0.2426
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 268.26829 on 7 degrees of freedom
## Residual deviance: 3.18361 on 5 degrees of freedom
## AIC: 37.9621
##
## Number of Fisher Scoring iterations: 4加入了濃度平方以後,該項本身的 Wald 檢驗結果告訴我們,沒有證據證明濃度和昆蟲死亡比例的對數比值比之間呈拋物線關系。
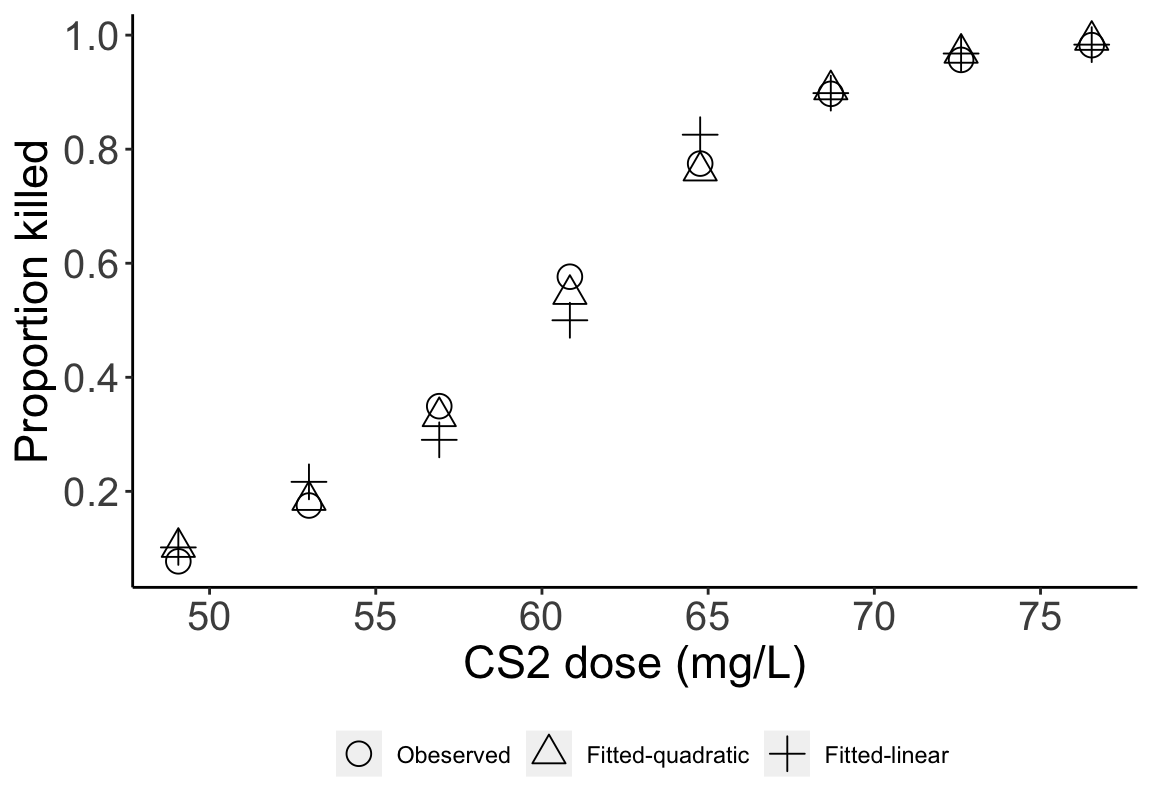
圖 59.4: Fitted probabilities for each dose from two models
加入濃度平方二次項的模型在第三和第四組給出了比一次模型更加接近觀測值的估計。但是這種提升是極爲有限的,且統計學上加入的二次項的回歸系數並無意義。
所以,本數據分析的結論是,有很強的證據證明昆蟲死亡的概率隨着CS2 濃度的升高而升高 (P<0.001)。死亡的比值 (odds),隨着濃度每升高1個單位 (mg/l) 而升高 27% (95% CI: 22%-32%)。
59.6.2 哮喘門診數據
在一項橫斷面研究中,訪問哮喘門診連續達到 6 個月以上的全部患者被一一詢問其目前的用藥情況和症狀。下面的表格總結的是這些患者中,目前使用口服類固醇藥物與否,及患者報告夜間由於哮喘症狀而從睡眠中醒來的次數。
| Corticosteroids | Never | Less.than.once.a.week | More.than.once.a.week | Every.night |
|---|---|---|---|---|
| User | 27 | 41 | 44 | 38 |
| Non-user | 20 | 10 | 8 | 22 |
下面的 STATA 輸出報告,是對上述數據擬合的邏輯回歸的結果。其中變量 user 和 never 被編碼爲 0/1,1 代表該患者正在使用口服類固醇藥物,或者從未因爲哮喘而在夜間醒來。變量 sev 是患者自己報告的哮喘症狀嚴重程度 (0-3 分,分數越高症狀越嚴重)。
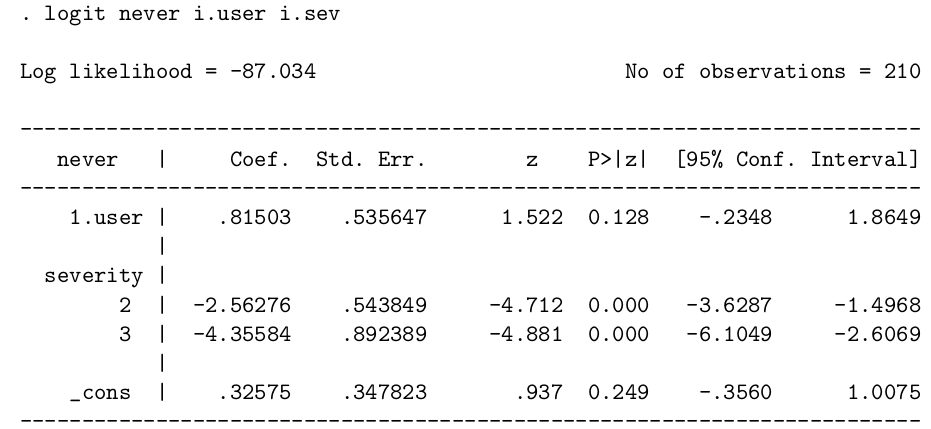
- 用表格的數據實施了一個總體的卡方檢驗還有一個卡方檢驗的傾向性檢驗。這兩個卡方檢驗的統計量分別是 12.87, 和 0.25。請解釋這兩個統計量的實際含義。
在零假設 – 使用口服類固醇藥物和夜間因爲哮喘而醒來次數之間沒有關系 – 條件下,表格總體的卡方檢驗服從 \(\chi^2_3\) 分布。查表或者在 R 裏使用
## [1] 0.0049263406可以知道 p = 0.005。這是極強的反對零假設的證據。
相反,卡方檢驗的傾向性檢驗結果是 p = 0.62,這個結果提示使用類固醇藥物所佔的比例沒有傾向性:
## [1] 0.61707508兩個卡方檢驗的顯著不同應是因爲用類固醇藥物的患者比例在 “從不”, “低於每周一次”,“多餘每周一次” 中遞增,但是到了最後一組 “每天” 時又下降。傾向性檢驗比起總體的卡方檢驗在關系是單調遞增或者單調遞減時統計學效能更好,但是當關系變得復雜以後,傾向性卡方檢驗變得不再有優勢。傾向性檢驗其實等同於用一個變量 (用藥與否) 和另一個變量 (夜間因爲哮喘醒來次數) 做線性回歸。對於這個表格的數據來說,這是一個 U 型的關系,所以做線性回歸的結果也是會給出沒有意義的 p 值。
- 利用 STATA 的邏輯回歸報告,能對哮喘的嚴重程度和患者報告夜間從未因爲哮喘醒來(never wake up)之間的關系作出怎樣的結論?
從 STATA 計算的結果來看,該數據提供了極強的證據證明哮喘的嚴重程度和報告從未因哮喘而醒來之間呈負相關。特別地,哮喘嚴重程度爲 2 的患者比 1 的患者報告從未醒來的比值比 (odds ratio) 是 0.077 (95% CI: 0.027, 0.224, p < 0.001); 哮喘嚴重程度爲 3 的患者 比 1 的患者報告醒來的比值比是 0.0128 (95% CI: 0.0022, 0.0738, p < 0.001)。所以,哮喘越嚴重,報告夜裏從未醒來的概率越低。
- 利用 STATA 的邏輯回歸報告,能對是否使用口服類固醇藥物和報告從未因哮喘而醒來之間的關系作出怎樣的結論?
如果要計算未調整的比值比,我們可以把表格中第2-4列的數據合並,那麼在使用類固醇藥物的患者 (n = 150) 中 27 人報告從未醒來,在不使用類固醇藥物的患者中 (n = 60),有 20 人報告從未醒來。這樣未調整的比值比就是 \(\frac{27 \times 40}{20 \times 123} = 0.44\)。STATA 計算的邏輯回歸模型的結果顯示,這一數字在調整了哮喘症狀之後,發生了本質的變化: \(e^{0.815} = 2.26\)。雖然調整後的比值比並沒有統計學意義。但是它從小於 1 變成了大於 1,方向上發生了轉變。所以,調整了哮喘嚴重程度之後,數據似乎提示使用類固醇藥物和報告從不在夜間因哮喘醒來的概率呈正相關 (用藥者睡得更好),但是這個相關性沒有統計學意義,其95%信賴區間很寬。
- 從這些分析來看,哮喘嚴重程度和是否口服類固醇藥物之間有什麼樣的關系?
因爲用類固醇藥物和報告夜間不曾醒來在調整了哮喘嚴重程度之後從原先的負相關變成了正相關。又因爲哮喘嚴重程度本身和報告夜間不曾醒來之間是負相關,所以,是否口服類固醇藥物和哮喘嚴重程度之間呈正相關,也就是哮喘越嚴重,患者越傾向於使用類固醇藥物。