第 106 章密度估計 Density estimation - 狄雷克雷過程模型 DP models

這裏我們來探討如何在密度估計 (density estimation) 中使用非參貝葉斯 (BNP) 模型。主要介紹狄雷克雷過程的先驗概率在 BNP 模型中的應用。狄雷克雷過程是目前最常見的BNP。它主要有兩種類型：狄雷克雷過程混合模型 Dirichlet process mixture modeling，和有限狄雷克雷過程 finite Dirichlet process。

密度估計是常見的需要對來自陌生分佈 \(G\) 的獨立同分佈 (i.i.d) 樣本進行推斷時的過程：

\[ \begin{equation} y_i | G \stackrel{i.i.d}{\sim} G, i = 1, \dots,n \tag{106.1} \end{equation} \]

當我們需要對該過程使用貝葉斯理論推斷時，我們需要給 \(G\) 補充一個先驗概率分佈 \(\pi\)。假設這個 \(G\) 的先驗概率分佈需要無限維度參數，也就是需要一個 BNP 先驗概率。

106.1 狄雷克雷過程 Dirichlet process

106.1.1 定義 definition

狄雷克雷過程先驗概率 (DP prior) 是最常見的 BNP 模型。它最早由 Ferguson (1973) 作爲測度概率空間的先驗概率分佈提出 (as a prior on the space of probability measures)。

Definition 106.1 (Dirichlet process-DP) 令 \(M > 0\) 且 \(G_0\) 是定義在空間 \(S\) 上的概率測度 (probability measure)。一個 DP 過程的參數由 \((M, G_0)\) 構成。該過程是定義在空間 \(S\) 上的一個隨機概率測度，對於任意一個可以測量的子集 \(B\) 賦予對應的概率 \(G(B)\)。\(\{ B_1, \dots, B_k \}\) 構成了整個空間 \(S\)。那麼這些子集的聯合概率分佈 joint distribution \((G(B_1), \dots, G(B_k))\) 是一個狄雷克雷分佈，它的參數表達如下： \[ (MG_0(B_1), MG_0(B_2), \dots, MG_0(B_k)) \]

這個 DP 過程又可簡寫爲 DP\((MG_0)\)，或者 DP\((M,G_0)\)。其中參數 \(M\) 叫做精確度 (precision) 或者總量參數 (total mass parameter)。參數 \(G_0\) 則又叫做中心測度 (centering measure)，他們的乘積 \(\alpha \equiv MG_0\) 被叫做狄雷克雷過程的基礎測度 (base measure)。

狄雷克雷過程一個重要性質是 \(G\) 的離散特性 (discrete nature)。由於是一個離散型隨機概率測度，我們總是可以把 \(G\) 改寫成是每個測量位點的權重之和 (sum of point masses)：\(G(\cdot) = \sum_{h = 1}^\infty w_h \delta_{m_h}(\cdot)\)。這個權重之和中，\(w_1, w_2, \dots\) 就是概率權重，\(\delta_x(\cdot)\) 標記的是 \(x\) 的狄拉克位置測度 (Dirac measure at \(x\))。狄雷克雷另一個重要性質是它強大的極微小支持 (largely weak support)。這意味着，在較爲溫和的條件下，任意的分佈都可以通過中心測度 \(G_0\)，和隨機概率測度模擬和近似 (well approximated)。

掰棍子過程 (stick-breaking process) 是利用狄雷克雷過程中 \(G(\cdot)\) 的離散性質，即 \(G(\cdot) = \sum_{h = 1}^\infty w_h \delta_{m_h} (\cdot)\)。在掰棍子過程中，位置函數 \(m_h\) 是從中心測度 \(G_0\) 中隨機採集的 i.i.d 樣本。每一個權重 \(w_h\) 是被定義爲剩餘長度棍子中的一部分 (a fraction of what is left after the proceeding point mass)：\(\{ 1- \sum_{\ell < h} W_\ell \}\)。令 \(w_h = v_h \prod_{\ell < h}(1 - v_\ell)\)，且 \(v_h \stackrel{i.i.d}{\sim} \text{Beta}(1, M)\)，\(m_h \stackrel{i.i.d}{\sim} G_0\)，\(\{ v_h \}, \{ m_h \}\) 之間相互獨立。那麼就定義隨機概率測度 DP\((MG_0)\) 爲：

\[ \begin{equation} G(\cdot) = \sum_{h = 1}^\infty w_h \delta_{m_h} (\cdot) \tag{106.2} \end{equation} \]

這樣表達的話， \(G \sim \mathbf{DP}(MG_0), m \sim G_0, W \sim \text{Beta}(1, M)\) 會使 \(W\delta_m(\cdot) + (1 - W) G(\cdot)\) 本身仍然是一個 DP\((MG_0)\) 的分佈。

106.1.2 推導

Special thanks to Professor Yida Xu. 特別鳴謝徐亦達教授，免費提供了狄雷克雷過程的詳細講解視頻。

假如有樣本量是 \(N\) 的一組觀察數據 \(x_1, x_2, x_3, \dots, x_i, \dots, x_N\)，這個數據中國每一個元素，對應產生它的分佈的相應參數是 \(\theta_1, \theta_2, \theta_3, \dots, \theta_i, \dots, \theta_N\)。如果 \(\theta_i \sim H(\theta)\) 是一個連續分佈，那麼該過程產生的 \(\theta\) 將不可能有相同的值，即 \(\text{Pr}(\theta_1 = \theta_2) = 0\)。

這時，我們思考，讓 \(\theta_i \sim G\) 是一個離散型 (discrete) 分佈。

\[ G \sim \mathbf{DP} (\alpha, H) \]

其中，\(\alpha\) 是一個大於零的標量 (scalar)，\(\alpha > 0\)。\(\alpha\) 決定了離散分佈 \(G\) 本身和連續分佈 \(H\) 之間相似程度，\(\alpha\) 越小，\(G\) 越離散，\(\alpha\) 越大，\(G\) 越接近 \(H\)，也就是越平滑（越連續）。當 \(\alpha\) 等於零，\(G\) 就離散到只剩下一個單一的值，也就是極端離散情況。反過來，\(\alpha \rightarrow \infty\) 時，\(G = H\)。當然這兩種極端情況是我們在使用 DP 時不太會採用的。

\(H\) 也可以使用離散分佈，並不一定非要是連續型分佈。

如果我們從某個分佈 \(x_i \sim P(X | \theta)\) 中採集樣本，我們只能得到一系列的觀測點，只是一個實現的值。但是如果 \(G \sim \mathbf{DP}(\alpha, H)\)，它產生的則不是一個個的值，而是隨機採集整個離散型的分佈, random discrete probability measure。如圖 106.1 所示的那樣，我們從一個 \(G \sim \mathbf{DP}(\alpha, H)\) 採集兩個 \(G_1, G_2\) 離散分佈，每個離散分佈之間互不相同，它們有各自的點，和每個點上”棍子”的長度，由於他們都是一個完整的離散分佈，那麼很顯然，每一次採集的 \(G\) 它的那些瑣碎的棍子的長度加起來都必須等於1。

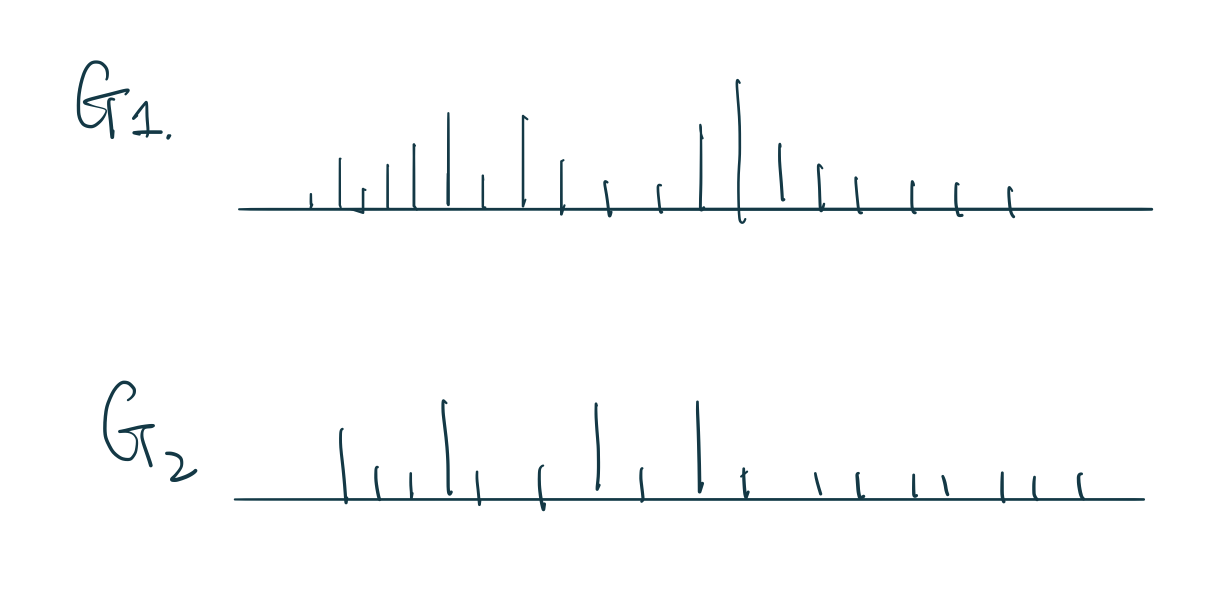
Sampling through Dirichlet Process is sampling random discrete probability measures for us, each sample is a whole discrete distribution.

圖 106.1: Sampling through Dirichlet Process is sampling random discrete probability measures for us, each sample is a whole discrete distribution.

如果在每次採集的隨機離散分佈 \(G\) 上有 \(a_1, a_2, a_3, \dots, a_d\) 個區域的話，如圖 106.2。那麼有 \(G(a_1), G(a_2), \dots, G(a_d) \sim \text{Dirichlet}(\alpha H(a_1), \alpha H(a_2), \dots, \alpha H(a_d))\)

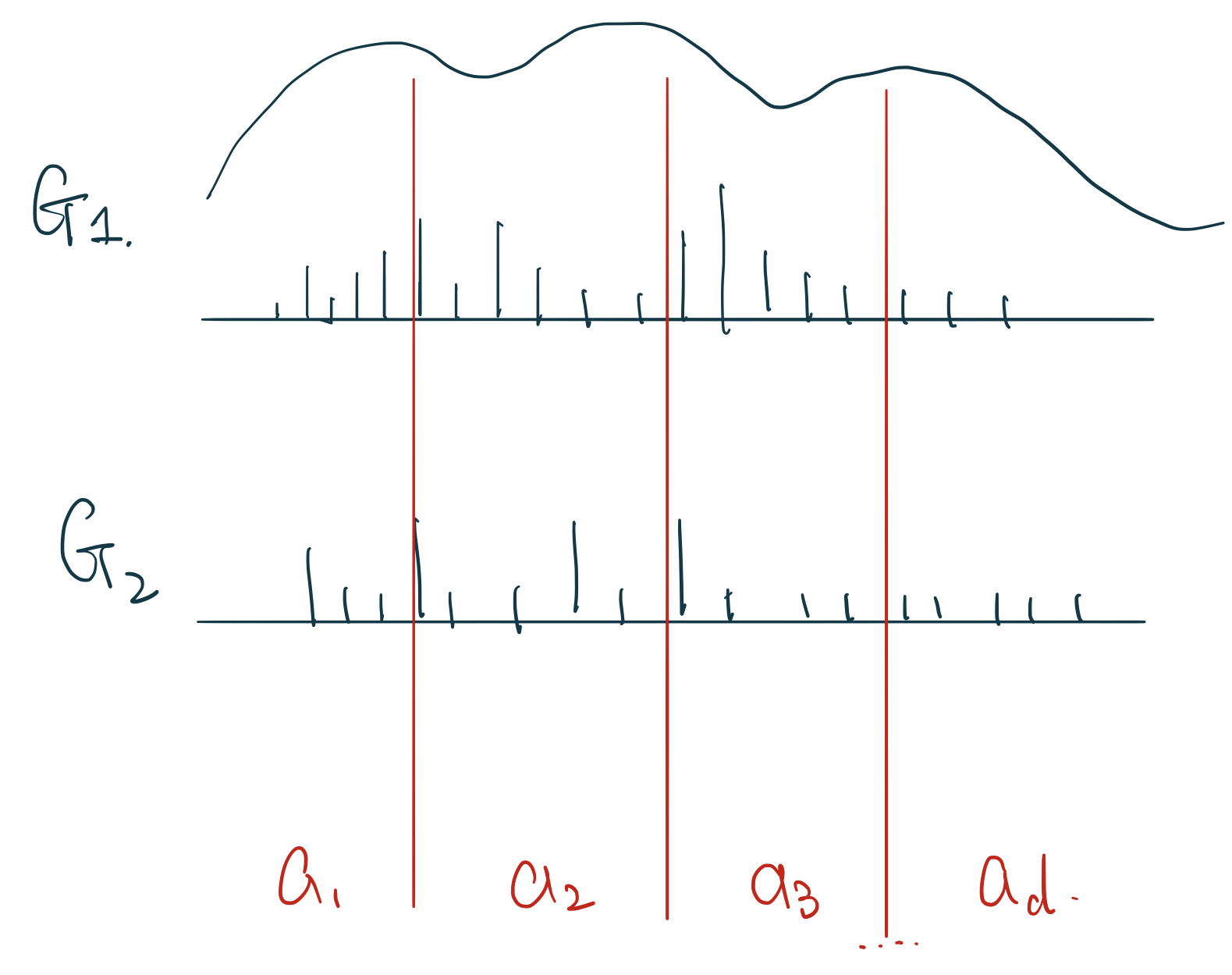
圖 106.2: G samples from the same Dirichlet Process with a series of partitions.

之前在貝葉斯統計學章節討論橫斷面研究時 (Chapter 100.3) 曾經使用果狄雷克雷分佈作爲一個先驗概率，當時提到果狄雷克雷分佈的一些性質。這裏重新再補充一下：

當 \(\text{Pr}(x_1, \dots, x_i, \dots, x_k) \sim \text{Dirichlet}(\alpha_1, \dots, \alpha_i, \dots, \alpha_k)\) 時，我們知道該分佈的期望（均值）和方差分別是：

\[ E[x_i] = \frac{\alpha_i}{\sum_k \alpha_k} \\ \text{Var}[x_i] = \frac{\alpha_i (\sum_k \alpha_k - \alpha_i)}{(\sum_k\alpha_k)^2(\sum_k\alpha_k + 1)} \]

根據狄雷克雷期望（均值）和方差的性質，圖 106.2 中任意一個區間(partition) \(a_i\) 上的期望（均值）和方差則分別可以被推導作是：

期望 \(E[G(a_i)]\):

\[ \begin{aligned} E[G(a_i)] & = \frac{\alpha H(a_i)}{\sum_k \alpha H(a_k)} \\ & = \frac{\alpha H(a_i)}{\alpha \sum_k H(a_k)} \\ \because & \sum_k H(a_k) = 1 \\ \therefore & = \frac{\alpha H(a_i)}{\alpha} \\ & = H(a_i) \end{aligned} \]

方差 \(\text{Var}[G(a_i)]\) :

\[ \begin{aligned} \text{Var}[G(a_i)] & = \frac{\alpha H(a_i)(\alpha - \alpha H(a_i))}{\alpha^2 (\alpha + 1)} \\ & = \frac{H(a_i)(1 - H(a_i))}{\alpha + 1} \\ \text{if } \alpha & \rightarrow \infty \text{ then } \\ \text{Var}[G(a_i)] & = 0 \\ \text{if } \alpha & \rightarrow 0 \text{ then } \\ \text{Var}[G(a_i)] & = H(a_i)(1 - H(a_i)) \end{aligned} \]

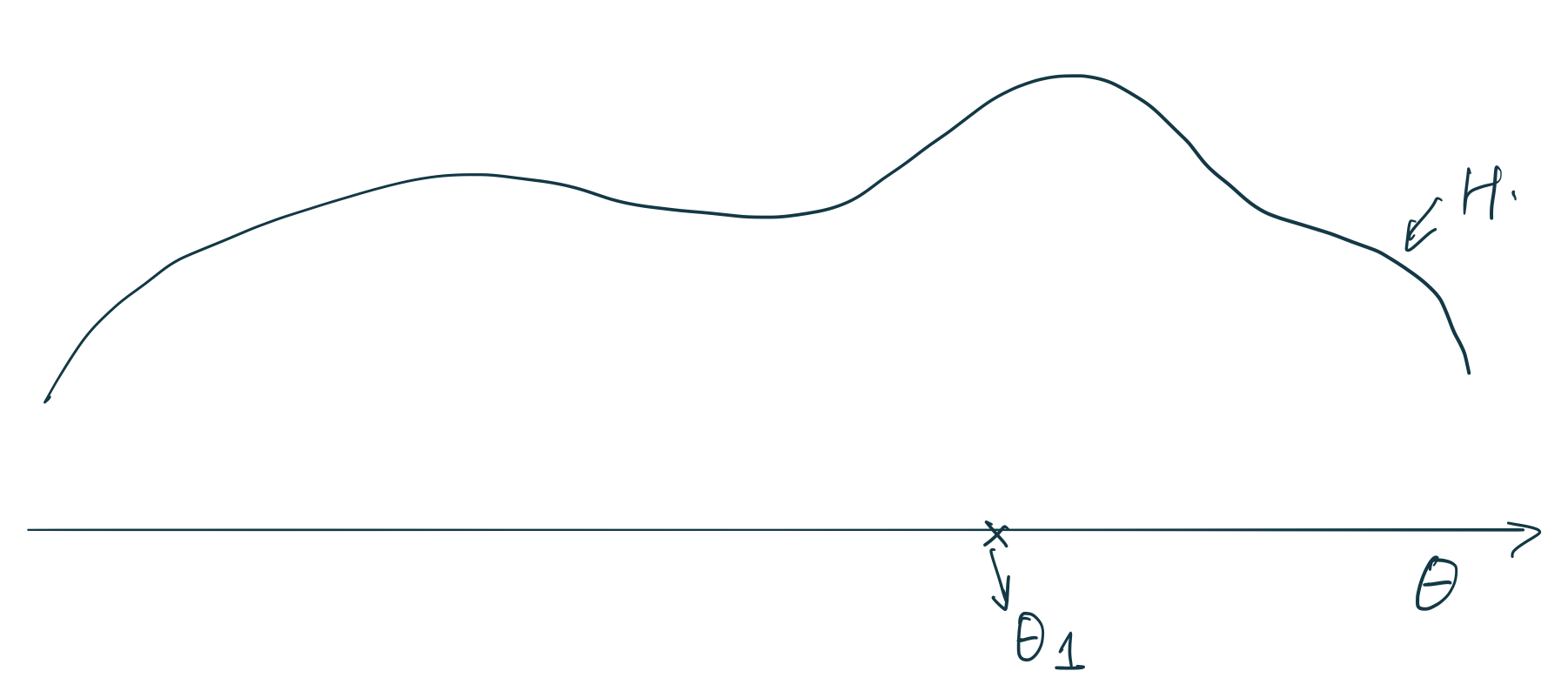
圖 106.3: Stick breaking construction (1).

圖 106.4: Stick breaking construction, weights from beta distribution (1).

那麼，狄雷克雷過程是怎樣進行測度採集的呢？下面詳述掰棍子構造 (stick-breaking construction) 的推導和理解。如圖 106.3 所示，橫軸是 \(\theta\)，有一個未知的連續型分佈 \(H\)。假如我們採集第一個原子 (atom) 在圖中的 \(\theta_1 \sim H\)。接下來DP要給這個原子分配一個權重 \(\pi_1\)。過程是通過 Beta 分佈 \(\pi_1 = \beta_1 \sim \text{Beta}(1, \alpha)\)。這裏的 Beta 分佈中的 \(\alpha\) 參數就是 DP\((\alpha, H)\) 過程中的 \(\alpha\) 參數。我們都知道 Beta 分佈是取值在 \(0\sim1\) 之間的一個特殊分佈 (詳見 Chapter 42.3.1 和 Chapter 96.2.2)。總結一下第一個原子的位點和權重的採集過程：

\[ \begin{aligned} \theta_1 & \sim H \\ \beta_1 & \sim \text{Beta}(1, \alpha) \\ \pi_1 & = \beta_1 \end{aligned} \]

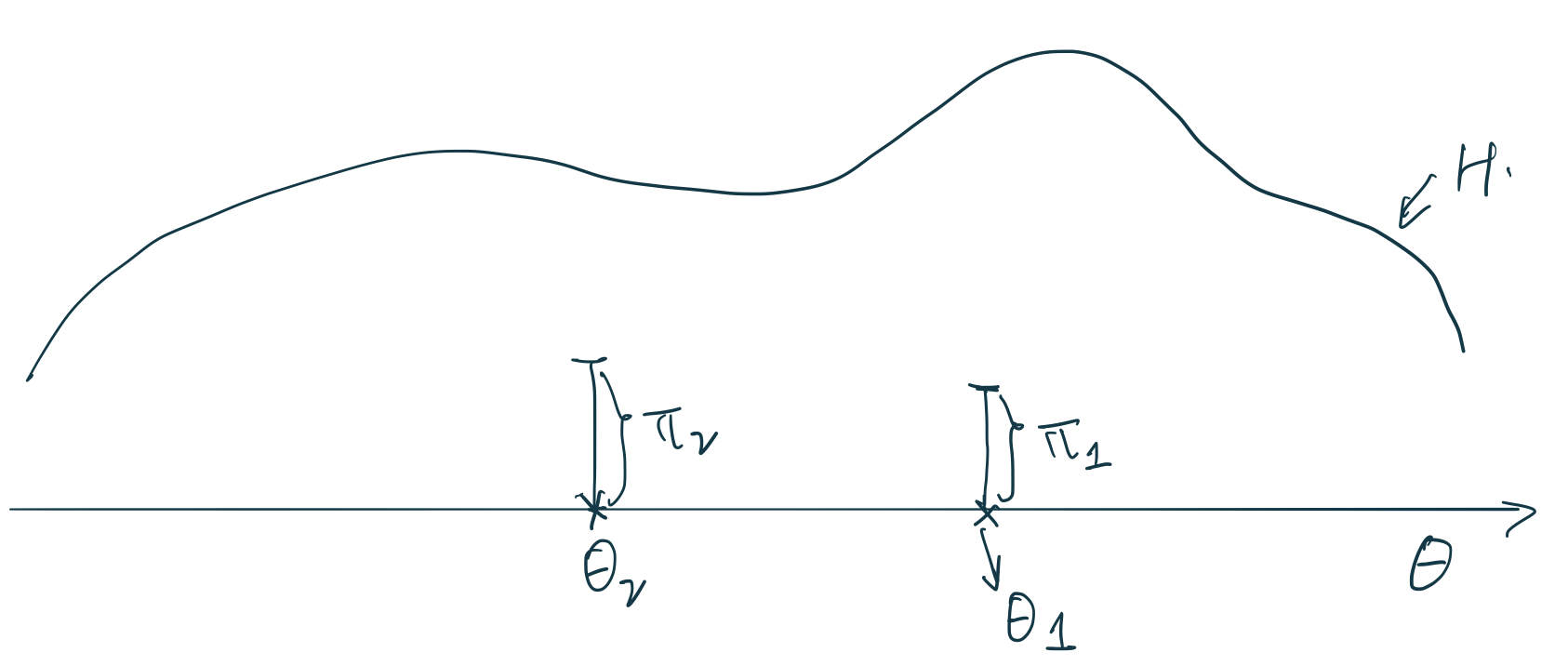
圖 106.5: Stick breaking construction (2).

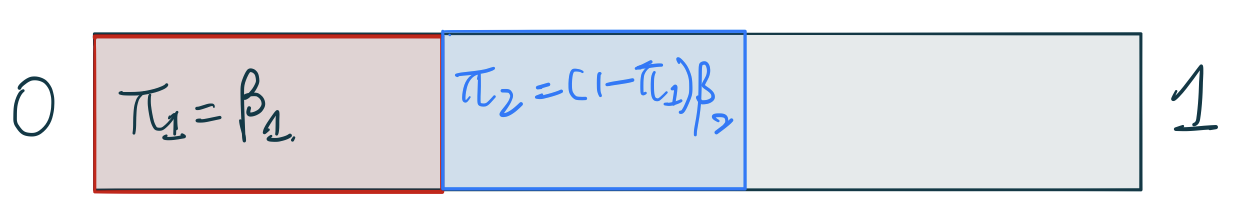
圖 106.6: Stick breaking construction, weights from beta distribution (2).

採集第二個 \(\theta_2\) 原子時它的位點假設如圖 106.5 中所示。它的權重 \(\pi_2\)，和第二次 Beta 分佈採集的 \(\beta_2\) 之間的關係是：\(\pi_2 = (1 - \pi_1)\beta_2\)，也就是第一次棍子掰掉以後剩餘的部分，乘以一個百分比作為第二次權重採樣的取值。總結一下第二個原子的位點和權重的採集過程：

\[ \begin{aligned} \theta_2 & \sim H \\ \beta_2 & \sim \text{Beta}(1, \alpha) \\ \pi_2 & = (1 - \pi_1)\beta_2 \end{aligned} \]

\(\theta_3, \theta_4, \dots\) 也就是依據相同的規則以此類推，直到完成一次 \(G\) 的測度全樣本採集。

106.1.2.1 性質

如圖 106.7 所示，無論我們給 \(H\) 作多少個區分 partitions，只要我們從它的分佈中採集狄雷克雷過程測度，有如下的結論：

\[ G \sim \mathbf{DP}(\alpha, H) \\ \Leftrightarrow (G(a_1), G(a_2), \dots, G(a_n)) \\ \Leftrightarrow \text{Dirichlet}(\alpha H(a_1), \dots, \alpha H(a_n)) \\ \forall \text{ partitions } a_1, \dots, a_n \]

如果說，每個測度點的位置是 \(\delta \theta_i\), 每個測度點的權重是 \(\pi_i\)，那麼有：

\[ G = \sum_{i = 1}^\infty \pi_i \delta\theta_i \]

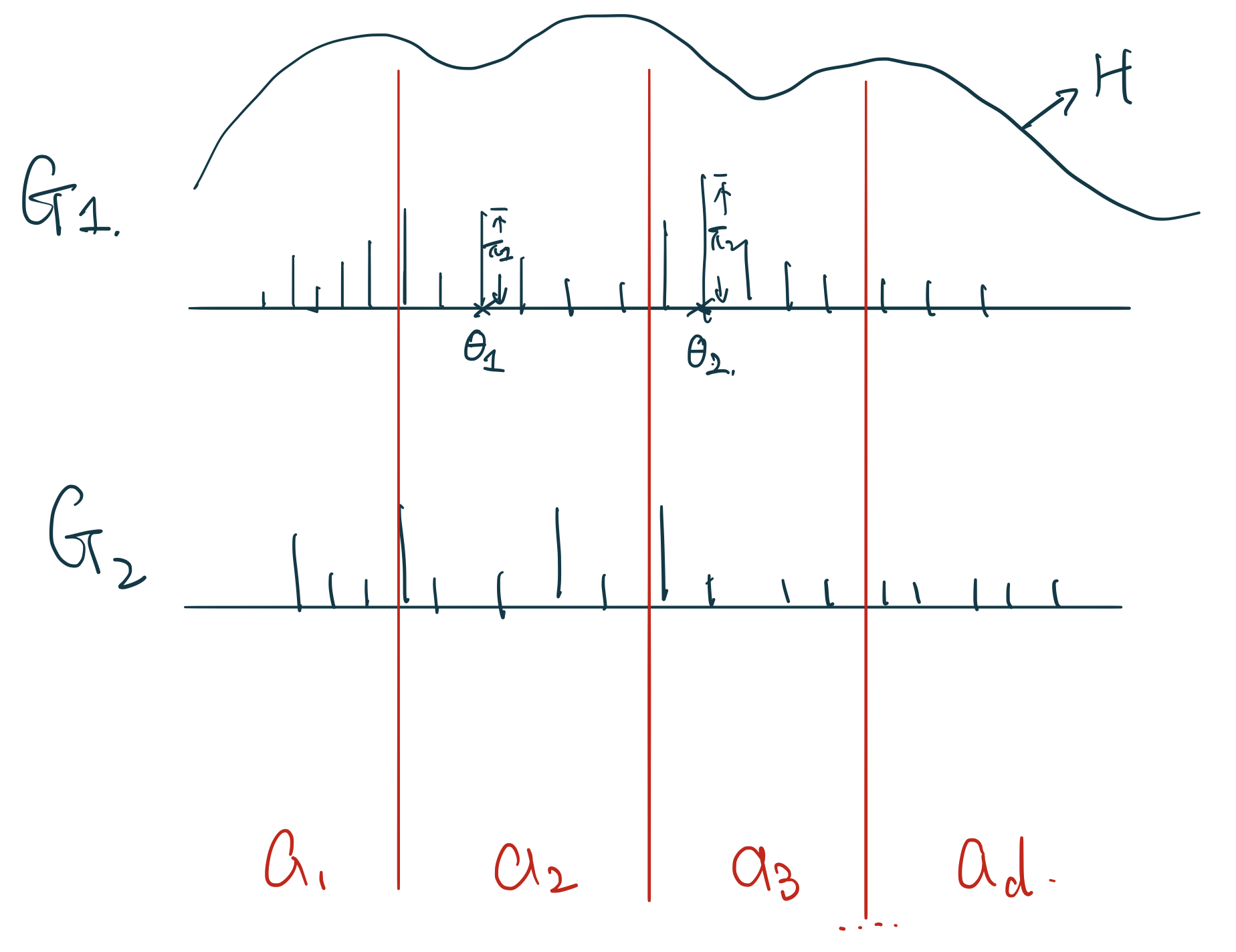
圖 106.7: The key properties for Gs sampled from a Dirichlet Process.

再繼續解釋狄雷克雷過程的性質之前，需要複習一下狄雷克雷分佈和多項式分佈的特徵。

假如有一個 \(k\) 維的離散分佈，服從狄雷克雷分佈：

\[ (P_1, P_2, \dots, P_k) \sim \text{Dirichlet}(\alpha_1, \alpha_2, \dots, \alpha_k) \\ \sum P_i = 1 \]

假如有一個組 \(k\) 個觀測數據，服從多項式分佈，該多項式的參數就是 \(P_1, \dots, P_k\)：

\[ (n_1, n_2, \dots, n_k) \sim \text{Multinomial}(P_1, P_2, \dots, P_k) \]

那麼事後概率分佈：

\[ \begin{aligned} \text{Pr}(P_1, \dots, P_k | n_1, \dots, n_k) & \propto \color{red}{\boxed{\text{Prior}}} \times \color{darkgreen}{\boxed{\text{Likelihood}}} \\ & \color{red}{\frac{\Gamma(\sum_{i = 1}^k \alpha_i)}{\prod_{i = 1}^k\Gamma (\alpha_i)} \prod_{i = 1}^k P_i^{(\alpha_i - 1)}} \times \\ & \color{darkgreen}{\frac{(\sum n_i)!}{n_1 ! n_2 ! \dots n_k !}\prod_{i = 1}^k P_i^{n_i}} \\ \text{Remove } & \text{those without } P_i, n_i\\ & \propto \prod_{i = 1}^k P_i^{(n_i + \alpha_i - 1)} \\ = \text{Dirichlet}(&\alpha_1 + n_1, \alpha_2 + n_2, \dots, \alpha_k + n_k) \end{aligned} \]

故我們發現當先驗概率分佈是狄雷克雷分佈，數據服從多項式分佈時，其事後概率分佈也是一個狄雷克雷分佈。這是一個共軛分佈(conjugate)的性質。

所以對於任意的區間 (partition)：

\[ \begin{aligned} \text{Pr}(G(a_1), G(a_2), \dots, G(a_k) & | n_1, n_2, \dots, n_k) \\ \propto \text{ Multinomial}(n_1, &\dots, n_k | G(a_1), \dots, G(a_k) ) \\ &\times \text{Dirichlet}(\alpha H(a_1), \dots, \alpha H(a_k)) \\ = \text{Dirichlet}(\alpha H(a_1) & + n_1, \dots, \alpha H(a_k) + n_k) \\ = \mathbf{DP}(\alpha + n, & \frac{\alpha H + \sum_{i = 1}^n \delta \theta}{\alpha +n}) \end{aligned} \]

106.1.3 事後概率分佈和邊際分佈

事後更新 posterior updating：狄雷克雷過程本身是共軛的 (conjugate)。也就是說，只要是按照獨立同分佈原則從模型 ((106.1)) 中進行 DP 採樣，獲得的事後概率分佈還是一個狄雷克雷 DP。

也就是說，如果令 \(y_1, \dots, y_n | G \stackrel{i.i.d}{\sim} G\) 且 \(G \sim \mathbf{DP}(M, G_0)\)，那麼，事後概率分佈爲：

\[ \begin{equation} G | y_1,\dots, y_n \sim \mathbf{DP}(M + n, \frac{MG_0 + \sum_{i = 1}^n \delta_{y_i}}{M + n}) \end{equation} \]

Example 106.1 T細胞受體個數問題 Guindani et al. (2014) 探討了計算T細胞受體個數和對應種類的問題。已知T細胞受體的種類和個數是免疫系統重要的指標之一。常見的分析該指標的方法是對受體集羣(clonal-size)計數，來評價其複雜程度 (diversity)。集羣分佈可以用統計表格計算集羣的頻率 \(\hat{G}_y, y = 1, 2, \dots, n\)。例如，\(\hat{G}_2 = 11\)，就表示有11個不同的T細胞受體集羣，每個集羣出現了2次。

下表展示了 \(\hat{G}_y\) 的觀察頻率，及其對應的計數 counts \(y_i = 1, 2, \dots\)。

Counts \(y_i\)	1	2	3	4	\(\geq\) 5
Frequencies	37	11	5	2	0

假如我們思考這樣一個模型 \(y_i \sim G\)，其中給集羣分佈(clonal size distribution)的先驗概率分佈是一個狄雷克雷過程分佈 \(G\sim\)DP\((MG_0)\)。由於計數型數據必須爲正(positive counts)，我們使用均值等於 2 的泊松分佈作爲中心測度 centering measure \(G_0 = \mathbf{Poi}(2)\)。總量參數 (total mass parameter) 使用 \(M =1\)。

下列採樣過程的代碼來自 https://rpubs.com/kaz_yos/dp1，你也可以參考原作者的網站

library(MCMCpack)
library(tidyverse)
tcell <- tribble(
    ~count, ~frequency,
    1, 37,
    2, 11,
    3, 5,
    4, 2,
    ## >= 5, 0,
    )
tcell

## # A tibble: 4 × 2
##   count frequency
##   <dbl>     <dbl>
## 1     1        37
## 2     2        11
## 3     3         5
## 4     4         2

# Prior

G0_vector <- function(lambda, min, max) {
    ## values below min are truncated
    ## values above max are collapsed

    ## Probabilities from Poisson(lambda) for min:max
    p_vec <- dpois(x = min:max, lambda = lambda)
    ## Probability for max+1 ...
    p_upper_tail <- 1 - ppois(q = max, lambda = lambda)
    ## Collapse to max
    p_vec[length(p_vec)] <- p_vec[length(p_vec)] + p_upper_tail
    ## Renormalize
    p_vec <- p_vec / sum(p_vec)
    ## Name
    names(p_vec) <- min:max
    ##
    return(p_vec)
}

## Collapse all values beyond 8 to 8+ bin
G0_vector(lambda = 2, min = 1, max = 8)

##            1            2            3            4            5            6            7 
## 0.3130352855 0.3130352855 0.2086901903 0.1043450952 0.0417380381 0.0139126794 0.0039750512 
##            8 
## 0.0012683748

References

Ferguson, Thomas S. 1973. “A Bayesian Analysis of Some Nonparametric Problems.” The Annals of Statistics, 209–30.

Guindani, Michele, Nuno Sepúlveda, Carlos Daniel Paulino, and Peter Müller. 2014. “A Bayesian Semi-Parametric Approach for the Differential Analysis of Sequence Counts Data.” Journal of the Royal Statistical Society. Series C, Applied Statistics 63 (3): 385.

第 106 章 密度估計 Density estimation - 狄雷克雷過程模型 DP models