第 50 章 模型選擇 model selection
50.1 預測變量越多越好嗎
50.1.1 變量越多總是會提高模型的擬合程度
過度擬合的實例 overfitting:下面的數據是一組關於類人猿平均腦容量和平均體重的數據。
sppnames <- c( "afarensis", "africanus", "habilis", "boisei",
"rudolfensis", "ergaster", "sapiens")
brainvolcc <- c(438, 452, 612, 521, 752, 871, 1350)
masskg <- c(37.0, 35.5, 34.5, 41.5, 55.5, 61.0, 53.5)
d <- data.frame( species = sppnames, brain = brainvolcc, mass = masskg)
d## species brain mass
## 1 afarensis 438 37.0
## 2 africanus 452 35.5
## 3 habilis 612 34.5
## 4 boisei 521 41.5
## 5 rudolfensis 752 55.5
## 6 ergaster 871 61.0
## 7 sapiens 1350 53.5不同種類的猿人中,體重和腦容量呈現高度相關性並不稀奇。我們更加關心的是,當考慮了體重大小之後,是否某些種類的猿人的腦容量比我們預期的要大很多?常見的解決方案是用一個把體重作為預測變量,腦容量作為結果變量的簡單線性回歸模型來描述該數據。我們現看看該數據的散點圖:
# with(d, plot(mass, brain,
# xlab = "body mass (kg)",
# ylab = "brain volumn (cc)"))
# library(ggrepel)
d %>%
ggplot(aes(x = mass, y = brain,
label = species),
ggtheme = theme_bw()) +
geom_point(color = rangi2) +
geom_text_repel(size = 5) +
labs(x = "body mass (kg)",
y = "brain volume (cc)") +
xlim(30, 65) +
theme(
axis.text = element_text(face = "bold",
color = "black",
size = 13),
axis.title = element_text(face = "bold",
color = "black",
size = 15)
)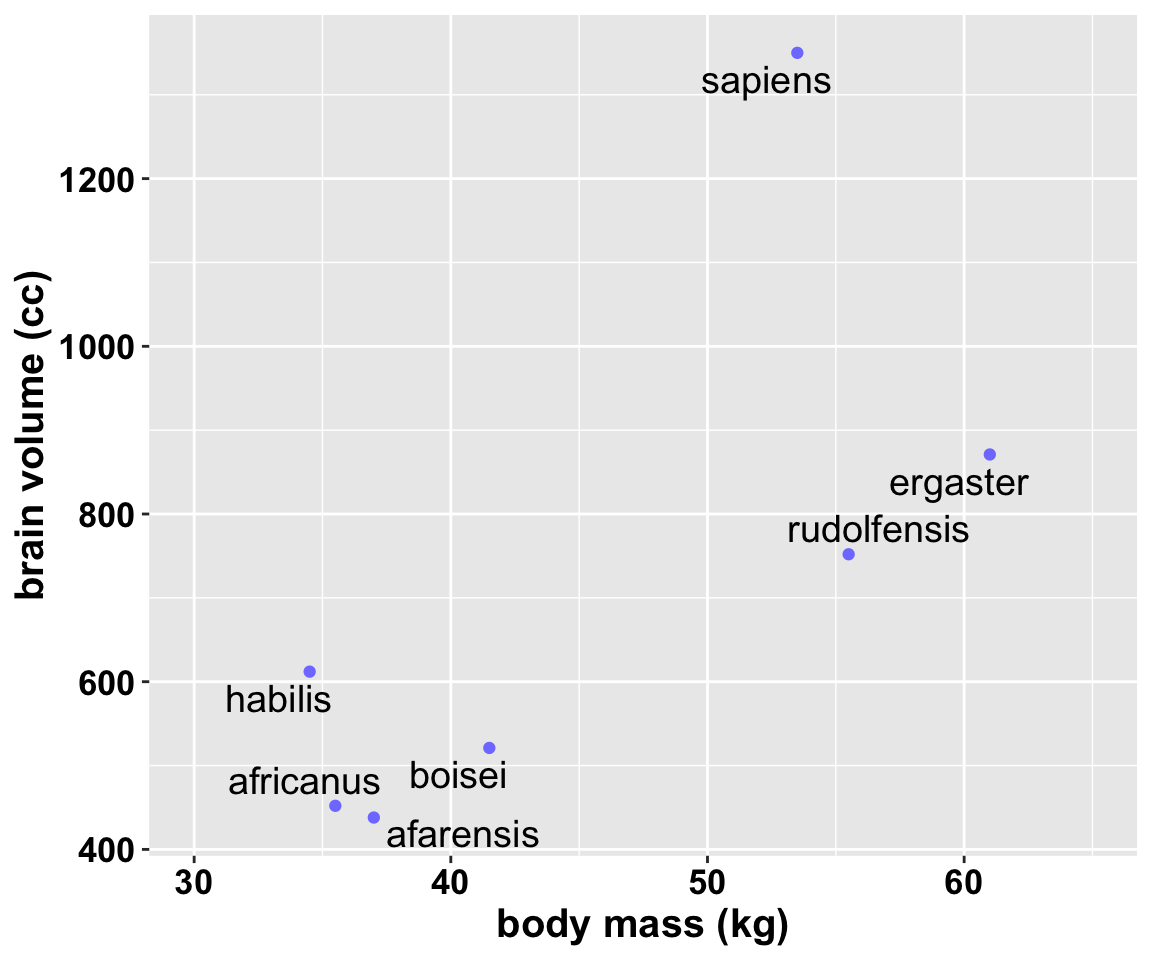
圖 50.1: Average brain volume in cubic centimeters against body mass in kilograms, for six hominin species. What model best describes the relationship between brain size and body size?
接下來我們來建立一系列越來越複雜的模型。最簡單的模型就是線性回歸模型。在建立模型之前,先把體重變量標準化,然後把腦容量變量的單位縮放一下成爲一個範圍是 0-1 的變量:
d$mass_std <- (d$mass - mean(d$mass)) / sd(d$mass)
d$brain_std <- d$brain / max(d$brain)
d## species brain mass mass_std brain_std
## 1 afarensis 438 37.0 -0.77946669 0.32444444
## 2 africanus 452 35.5 -0.91701964 0.33481481
## 3 habilis 612 34.5 -1.00872160 0.45333333
## 4 boisei 521 41.5 -0.36680786 0.38592593
## 5 rudolfensis 752 55.5 0.91701964 0.55703704
## 6 ergaster 871 61.0 1.42138044 0.64518519
## 7 sapiens 1350 53.5 0.73361571 1.00000000我們想要建立的第一個模型是這樣的:
\[ \begin{aligned} b_i & \sim \text{Normal}(\mu_i, \sigma) \\ \mu_i & = \alpha + \beta m_i \\ \alpha & \sim \text{Normal}(0.5, 1) \\ \beta & \sim \text{Normal}(0, 10) \\ \sigma & \sim \text{Log-Normal}(0, 1) \end{aligned} \]
m7.1 <- quap(
alist(
brain_std ~ dnorm( mu, exp(log_sigma) ),
mu <- a + b * mass_std,
a ~ dnorm( 0.5, 1 ),
b ~ dnorm( 0, 10 ),
log_sigma ~ dnorm( 0, 1 )
), data = d
)
precis(m7.1)## mean sd 5.5% 94.5%
## a 0.52854298 0.068425652 0.419185571 0.63790039
## b 0.16710917 0.074079702 0.048715501 0.28550284
## log_sigma -1.70670654 0.293780113 -2.176223904 -1.23718918# compared with traditional OLS estimation
m7.1_OLS <- lm(brain_std ~ mass_std, data = d)
summary(m7.1_OLS)##
## Call:
## lm(formula = brain_std ~ mass_std, data = d)
##
## Residuals:
## 1 2 3 4 5 6 7
## -0.073970 -0.040612 0.093232 -0.081451 -0.124891 -0.121031 0.348722
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.528677 0.070569 7.4916 0.0006697 ***
## mass_std 0.167118 0.076223 2.1925 0.0798469 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.18671 on 5 degrees of freedom
## Multiple R-squared: 0.49016, Adjusted R-squared: 0.38819
## F-statistic: 4.807 on 1 and 5 DF, p-value: 0.079847下面的代碼計算該模型 m7.1 的 \(R^2\)。
set.seed(12)
s <- sim( m7.1 )
r <- apply(s, 2, mean) - d$brain_std
resid_var <- var2(r)
outcome_var <- var2(d$brain_std)
1 - resid_var / outcome_var## [1] 0.47745889把上面的計算過程製作成一個函數,以便重複調用:
R2_is_bad <- function( quap_fit ){
set.seed(12)
s <- sim( quap_fit, refresh = 0)
r <- apply(s, 2, mean) - d$brain_std
1 - var2(r)/var2(d$brain_std)
}
R2_is_bad(m7.1)## [1] 0.47745889接下來,我們把這個模型擴展開,讓它更加複雜一些,增加一個二次項,試圖提升模型擬合度。
\[ \begin{aligned} b_i & \sim \text{Normal}(\mu_i, \sigma)\\ \mu_i & = \alpha + \beta_1 m_i + \beta_2 m_i^2 \\ \beta_j & \sim \text{Normal}(0, 10) & \text{for } j = 1, 2\\ \sigma & \sim \text{Log-Normal}(0,1) \end{aligned} \]
m7.2 <- quap(
alist(
brain_std ~ dnorm( mu, exp(log_sigma) ),
mu <- a + b[1] * mass_std + b[2] * mass_std^2,
a ~ dnorm(0.5, 1) ,
b ~ dnorm(0, 10),
log_sigma ~ dnorm(0, 1)
), data = d, start = list(b = rep(0, 2))
)
precis(m7.2, depth = 2)## mean sd 5.5% 94.5%
## b[1] 0.195147908 0.081147769 0.065458101 0.32483772
## b[2] -0.097978296 0.137571508 -0.317844137 0.12188754
## a 0.612177669 0.134474740 0.397261061 0.82709428
## log_sigma -1.749768093 0.294872400 -2.221031139 -1.27850505接下來,我們頭腦發熱狂加多次項到模型中去看會發生什麼:
m7.3 <- quap(
alist(
brain_std ~ dnorm( mu, exp(log_sigma) ),
mu <- a + b[1] * mass_std + b[2] * mass_std^2 +
b[3] * mass_std^3,
a ~ dnorm(0.5, 1) ,
b ~ dnorm(0, 10),
log_sigma ~ dnorm(0, 1)
), data = d, start = list(b = rep(0, 3))
)
m7.4 <- quap(
alist(
brain_std ~ dnorm( mu, exp(log_sigma) ),
mu <- a + b[1] * mass_std + b[2] * mass_std^2 +
b[3] * mass_std^3 + b[4] * mass_std^4,
a ~ dnorm(0.5, 1) ,
b ~ dnorm(0, 10),
log_sigma ~ dnorm(0, 1)
), data = d, start = list(b = rep(0, 4))
)
m7.5 <- quap(
alist(
brain_std ~ dnorm( mu, exp(log_sigma) ),
mu <- a + b[1] * mass_std + b[2] * mass_std^2 +
b[3] * mass_std^3 + b[4] * mass_std^4 +
b[5] * mass_std^5,
a ~ dnorm(0.5, 1) ,
b ~ dnorm(0, 10),
log_sigma ~ dnorm(0, 1)
), data = d, start = list(b = rep(0, 5))
)
m7.6 <- quap(
alist(
brain_std ~ dnorm( mu, exp(log_sigma) ),
mu <- a + b[1] * mass_std + b[2] * mass_std^2 +
b[3] * mass_std^3 + b[4] * mass_std^4 +
b[5] * mass_std^5 + b[6] * mass_std^6,
a ~ dnorm(0.5, 1) ,
b ~ dnorm(0, 10),
log_sigma ~ dnorm(0, 1)
), data = d, start = list(b = rep(0, 6))
)然後我們繪製上述每個模型給出的回歸線及其89%可信區間:
post <- extract.samples( m7.1 )
mass_seq <- seq( from = min(d$mass_std), to = max(d$mass_std),
length.out = 100)
l <- link( m7.1, data = list(mass_std = mass_seq))
mu <- apply(l, 2, mean)
ci <- apply(l, 2, PI)
plot( brain_std ~ mass_std, data = d,
main = "m7.1: R^2 = 0.48",
bty="n",
col = rangi2,
xaxt = "n",
yaxt = "n",
pch = 16,
xlab = "body mass (kg)",
ylab = "brain volumn (cc)")
at <- c(-2, -1, 0, 1, 2)
labels <- at*sd(d$mass) + mean(d$mass)
at_y <- seq(0.2, 1, by = 0.1)
labels_y <- at_y * max(d$brain)
axis( side = 2, at = at_y, labels = round(labels_y, 1))
axis( side = 1, at = at, labels = round(labels, 1))
lines( mass_seq, mu)
shade(ci, mass_seq)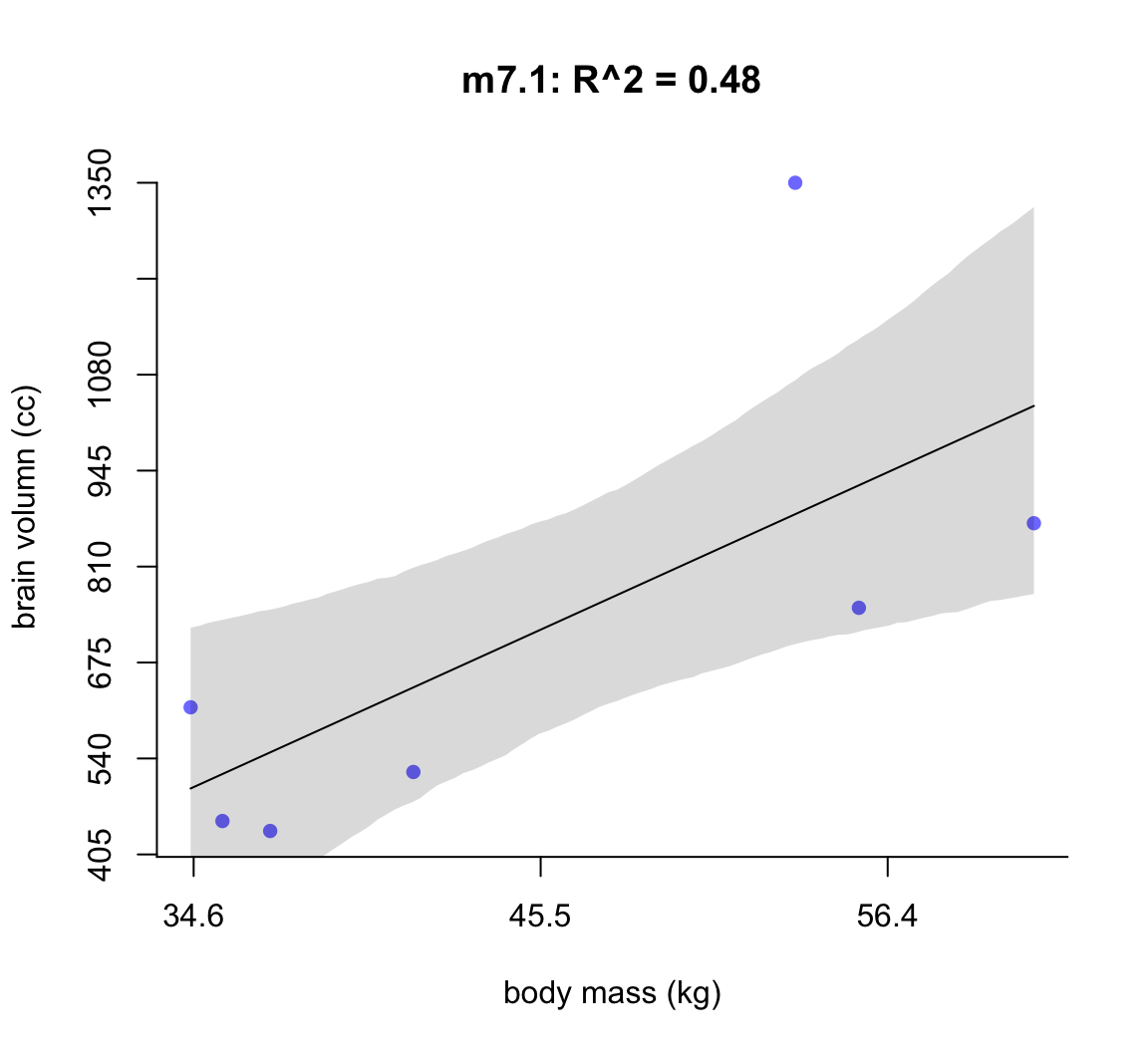
圖 50.2: Linear model of increasing degree for the hominin data. The posterior mean in black, with 89% interval of the mean shaded. R^2 is diplayed.
50.1.1.1 m7.2
post <- extract.samples( m7.2 )
mass_seq <- seq( from = min(d$mass_std), to = max(d$mass_std),
length.out = 100)
l <- link( m7.2, data = list(mass_std = mass_seq))
mu <- apply(l, 2, mean)
ci <- apply(l, 2, PI)
plot( brain_std ~ mass_std, data = d,
main = "m7.2: R^2 = 0.53",
bty="n",
col = rangi2,
xaxt = "n",
yaxt = "n",
pch = 16,
xlab = "body mass (kg)",
ylab = "brain volumn (cc)")
at <- c(-2, -1, 0, 1, 2)
labels <- at*sd(d$mass) + mean(d$mass)
at_y <- seq(0.2, 1, by = 0.1)
labels_y <- at_y * max(d$brain)
axis( side = 2, at = at_y, labels = round(labels_y, 1))
axis( side = 1, at = at, labels = round(labels, 1))
lines( mass_seq, mu)
shade(ci, mass_seq)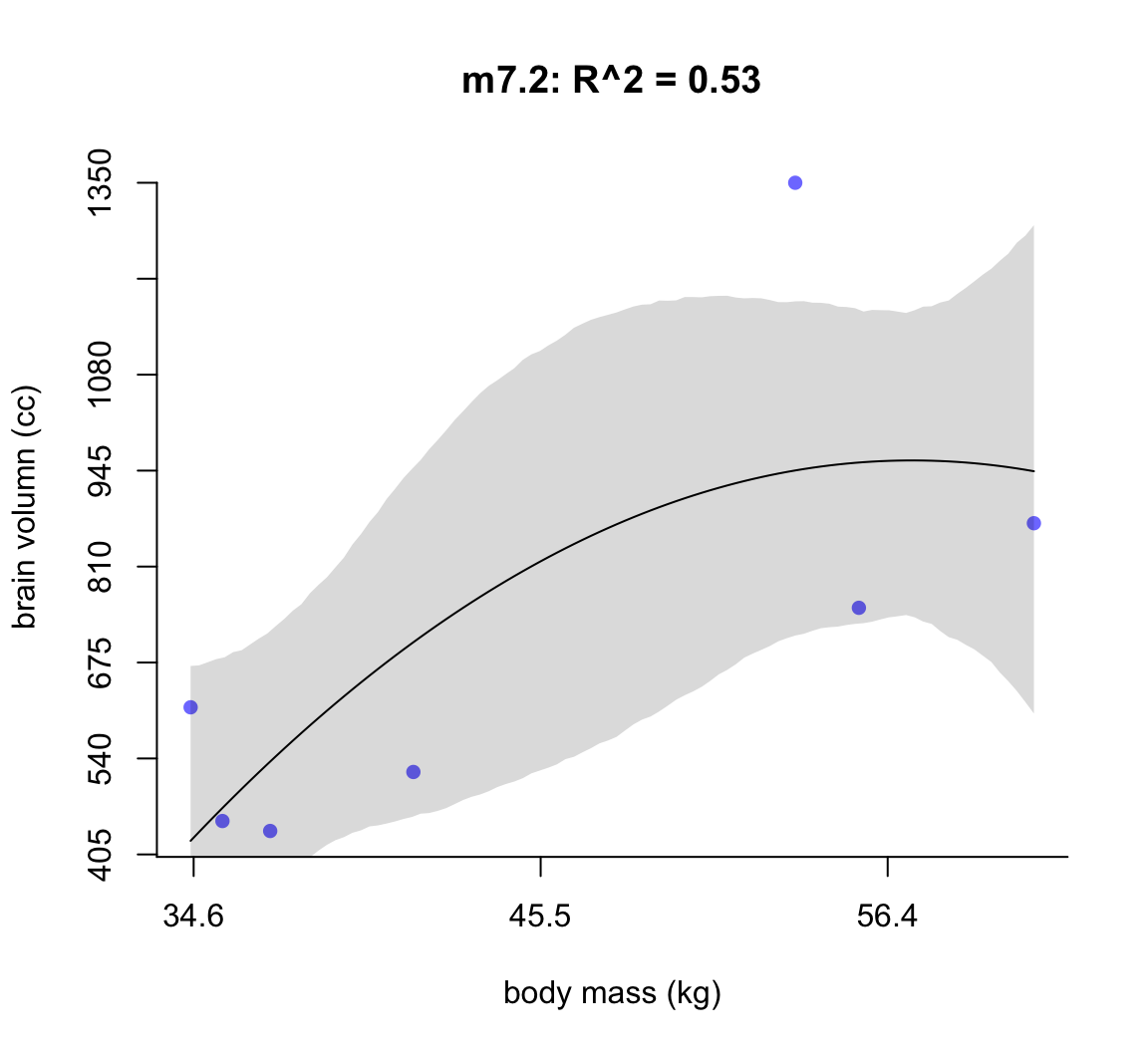
圖 50.3: Second-degree polynomial linear model of increasing degree for the hominin data. The posterior mean in black, with 89% interval of the mean shaded. R^2 is diplayed.
50.1.1.2 m7.3
post <- extract.samples( m7.3 )
mass_seq <- seq( from = min(d$mass_std), to = max(d$mass_std),
length.out = 100)
l <- link( m7.3, data = list(mass_std = mass_seq))
mu <- apply(l, 2, mean)
ci <- apply(l, 2, PI)
plot( brain_std ~ mass_std, data = d,
main = "m7.3: R^2 = 0.68",
bty="n",
col = rangi2,
xaxt = "n",
yaxt = "n",
pch = 16,
xlab = "body mass (kg)",
ylab = "brain volumn (cc)")
at <- c(-2, -1, 0, 1, 2)
labels <- at*sd(d$mass) + mean(d$mass)
at_y <- seq(0.2, 1, by = 0.1)
labels_y <- at_y * max(d$brain)
axis( side = 2, at = at_y, labels = round(labels_y, 1))
axis( side = 1, at = at, labels = round(labels, 1))
lines( mass_seq, mu)
shade(ci, mass_seq)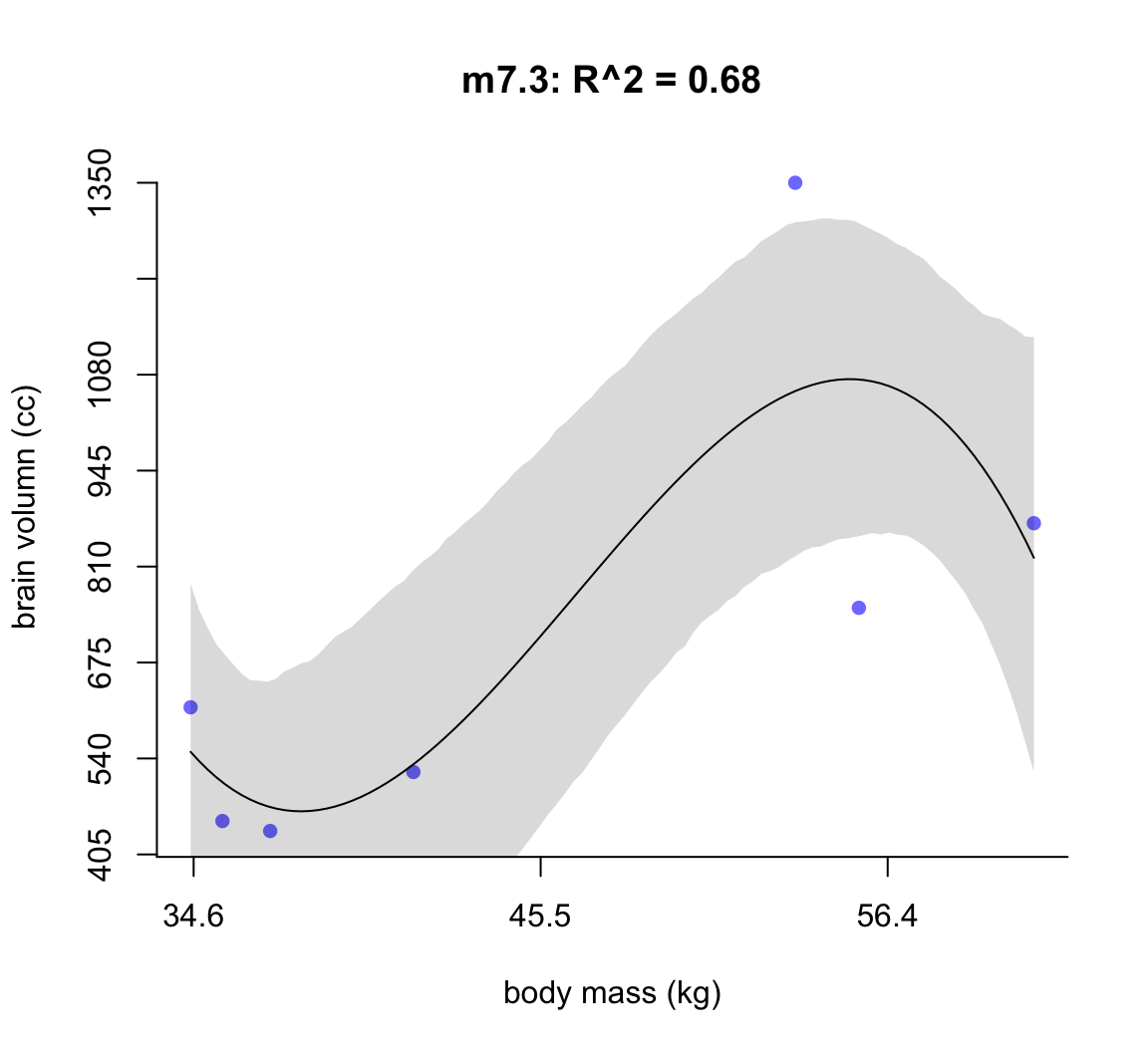
圖 50.4: Third-degree polynomial linear model of increasing degree for the hominin data. The posterior mean in black, with 89% interval of the mean shaded. R^2 is diplayed.
50.1.1.3 m7.4
post <- extract.samples( m7.4 )
mass_seq <- seq( from = min(d$mass_std), to = max(d$mass_std),
length.out = 100)
l <- link( m7.4, data = list(mass_std = mass_seq))
mu <- apply(l, 2, mean)
ci <- apply(l, 2, PI)
plot( brain_std ~ mass_std, data = d,
main = "m7.4: R^2 = 0.82",
bty="n",
col = rangi2,
xaxt = "n",
yaxt = "n",
pch = 16,
xlab = "body mass (kg)",
ylab = "brain volumn (cc)")
at <- c(-2, -1, 0, 1, 2)
labels <- at*sd(d$mass) + mean(d$mass)
at_y <- seq(0.2, 1, by = 0.1)
labels_y <- at_y * max(d$brain)
axis( side = 2, at = at_y, labels = round(labels_y, 1))
axis( side = 1, at = at, labels = round(labels, 1))
lines( mass_seq, mu)
shade(ci, mass_seq)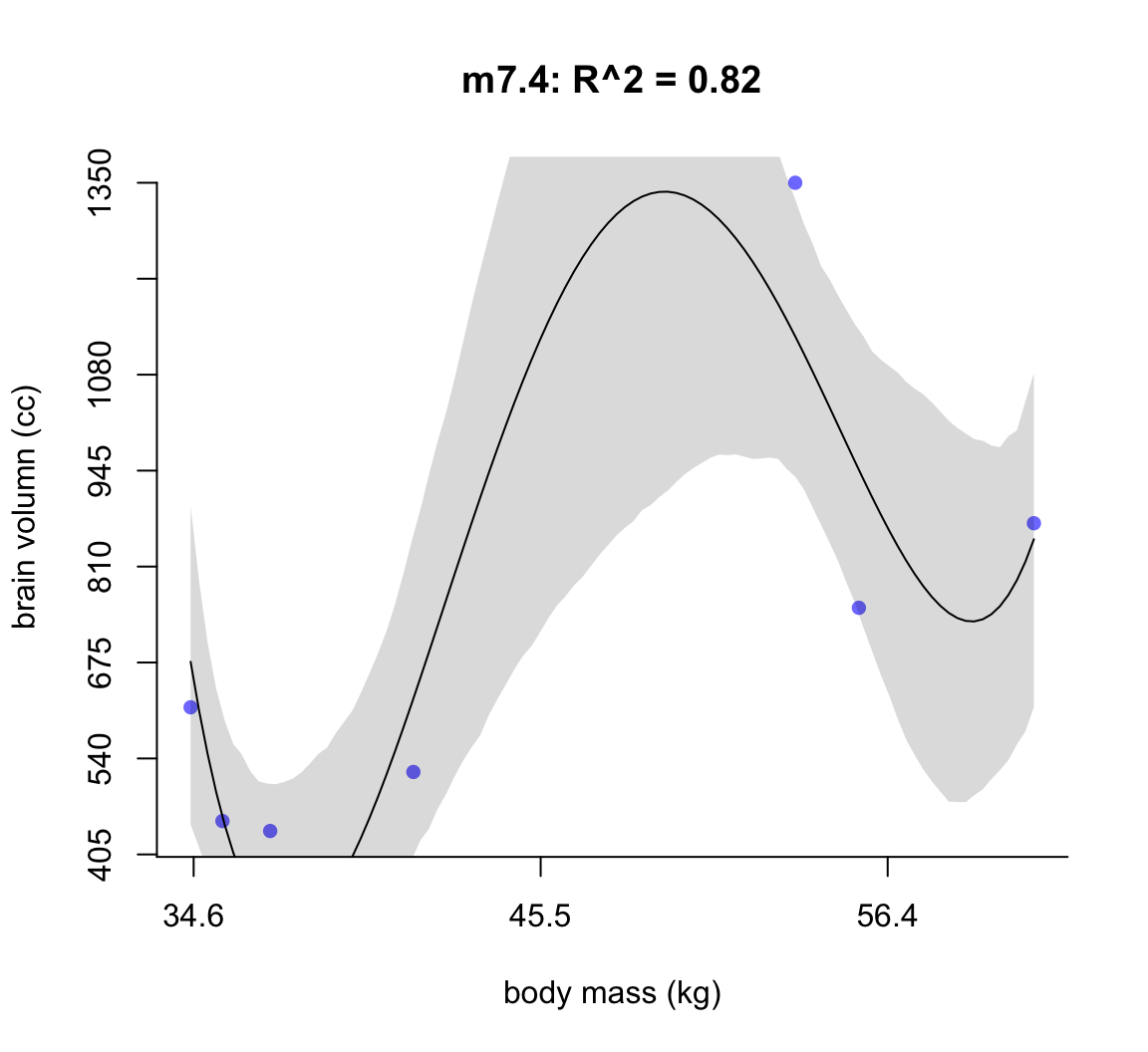
圖 50.5: Second-degree polynomial linear model of increasing degree for the hominin data. The posterior mean in black, with 89% interval of the mean shaded. R^2 is diplayed.
50.1.1.4 m7.5
post <- extract.samples( m7.5 )
mass_seq <- seq( from = min(d$mass_std), to = max(d$mass_std),
length.out = 100)
l <- link( m7.5, data = list(mass_std = mass_seq))
mu <- apply(l, 2, mean)
ci <- apply(l, 2, PI)
plot( brain_std ~ mass_std, data = d,
main = "m7.5: R^2 = 0.99",
bty="n",
col = rangi2,
xaxt = "n",
yaxt = "n",
pch = 16,
xlab = "body mass (kg)",
ylab = "brain volumn (cc)")
at <- c(-2, -1, 0, 1, 2)
labels <- at*sd(d$mass) + mean(d$mass)
at_y <- seq(0.2, 1, by = 0.1)
labels_y <- at_y * max(d$brain)
axis( side = 2, at = at_y, labels = round(labels_y, 1))
axis( side = 1, at = at, labels = round(labels, 1))
lines( mass_seq, mu)
shade(ci, mass_seq)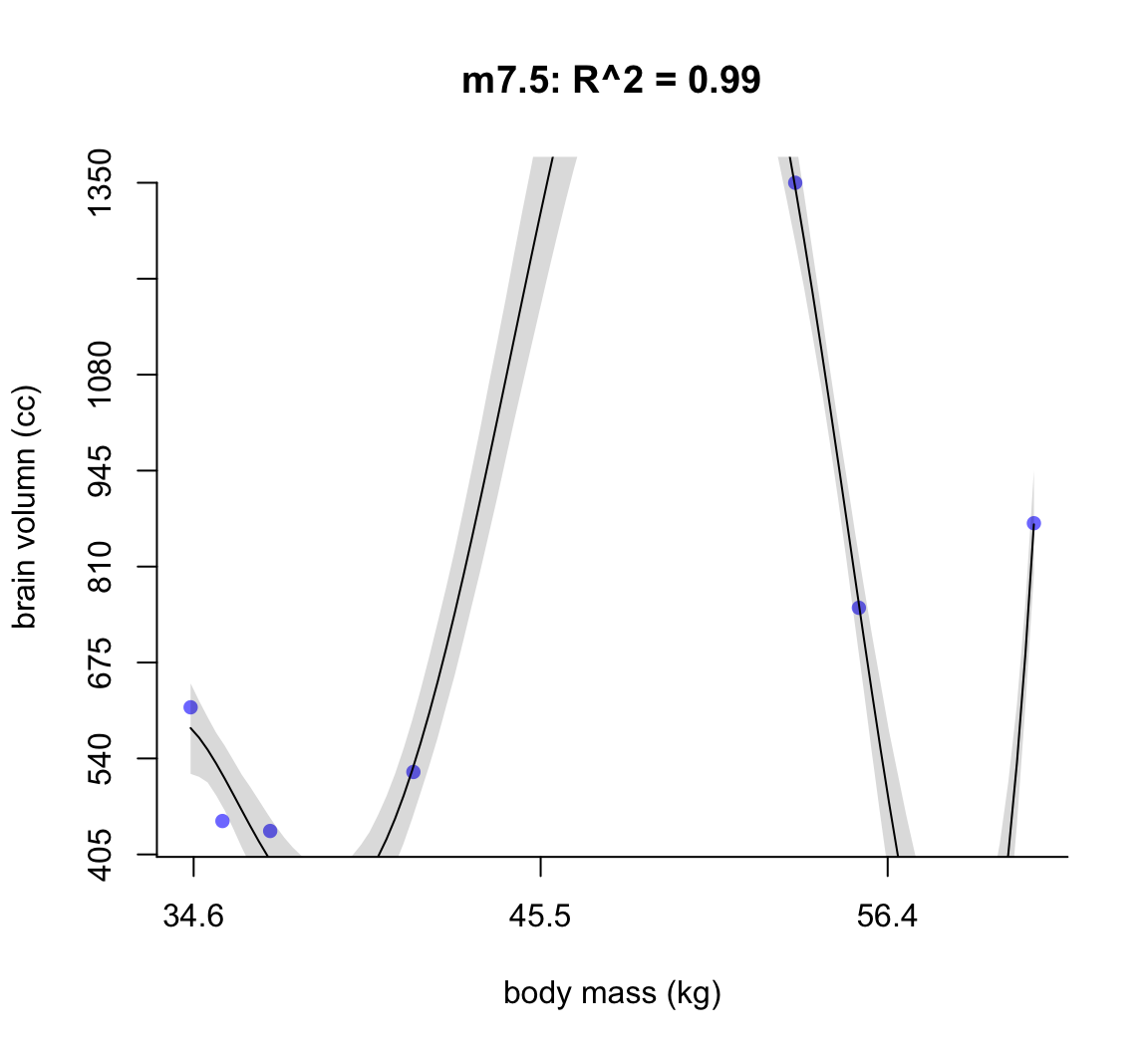
圖 50.6: Second-degree polynomial linear model of increasing degree for the hominin data. The posterior mean in black, with 89% interval of the mean shaded. R^2 is diplayed.
50.1.1.5 m7.6
post <- extract.samples( m7.6 )
mass_seq <- seq( from = min(d$mass_std), to = max(d$mass_std),
length.out = 100)
l <- link( m7.6, data = list(mass_std = mass_seq))
mu <- apply(l, 2, mean)
ci <- apply(l, 2, PI)
plot( brain_std ~ mass_std, data = d,
main = "m7.6: R^2 = 1",
bty="n",
col = rangi2,
xaxt = "n",
yaxt = "n",
pch = 16,
ylim = c(-0.3, 1.5),
xlab = "body mass (kg)",
ylab = "brain volumn (cc)")
at <- c(-2, -1, 0, 1, 2)
labels <- at*sd(d$mass) + mean(d$mass)
at_y <- seq(-0.3, 1.4, by = 0.1)
labels_y <- at_y * max(d$brain)
axis( side = 2, at = at_y, labels = round(labels_y, 1))
axis( side = 1, at = at, labels = round(labels, 1))
lines( mass_seq, mu)
shade(ci, mass_seq)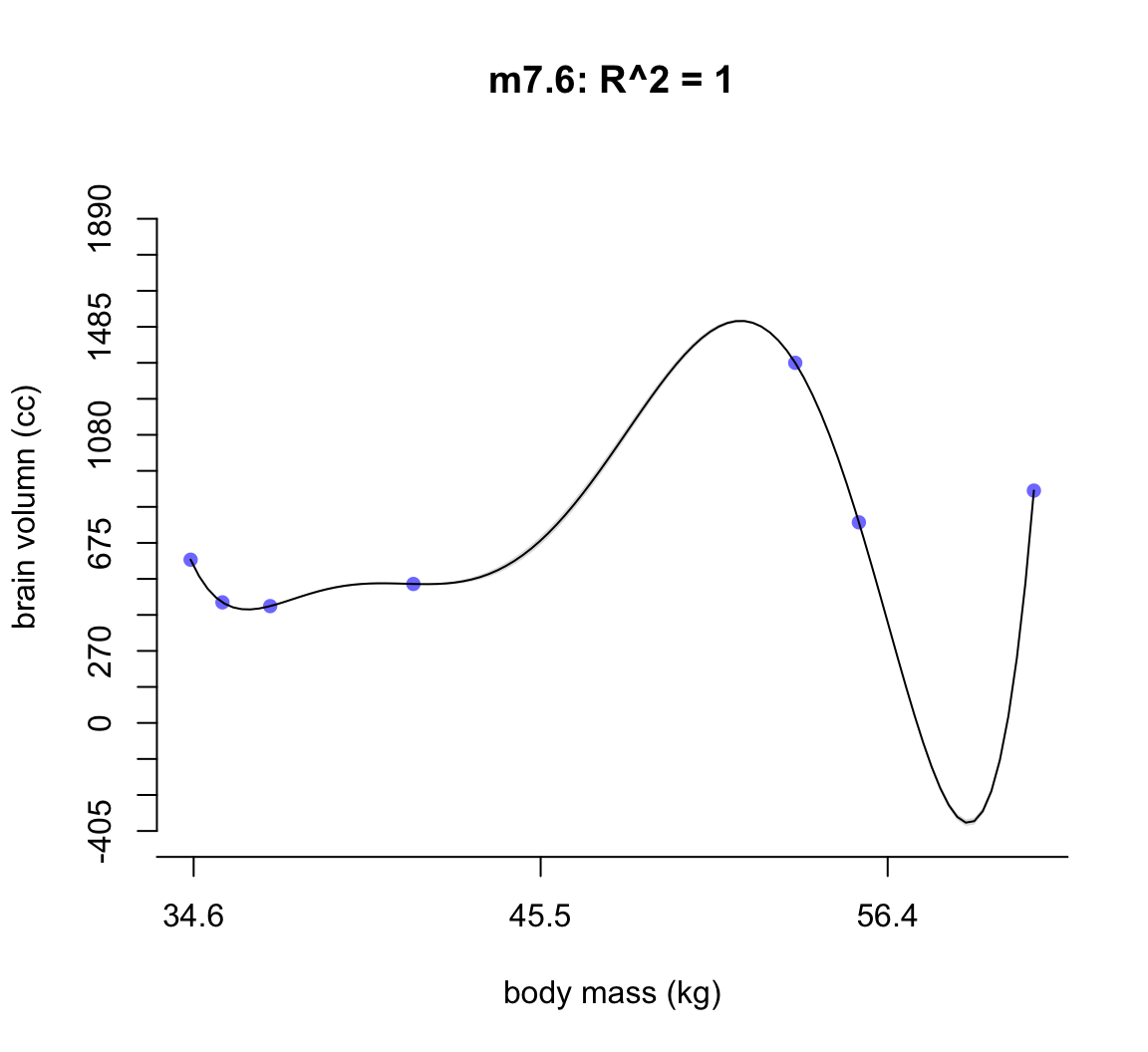
圖 50.7: Second-degree polynomial linear model of increasing degree for the hominin data. The posterior mean in black, with 89% interval of the mean shaded. R^2 is diplayed.
不難發現,當我們不斷地給模型增加多次項時,模型的擬合度,用 \(R^2\) 表示的話,是越來越接近完美的。但是最完美的模型 m7.6 給出了瘋狂的曲線,它完美的預測了每一個觀察數據。但是你不能相信這個模型對嗎,因為它竟然告訴我們當體重在 58 KG 時,腦容量是小於零的。這是極端的過擬合現象,overfitting。
50.1.2 也不是預測變量越少越好
過度擬合的模型,它的問題在於可以完美的告訴我們已有數據內的關係 (within sample accuracy),但是預測新數據的能力很差。與之相對應的,是擬合不足 (underfitting)。擬合不足的模型帶來的最大問題是,連已有的數據都無法準確地描述,更不要說用來預測了。
50.2 信息熵 information entropy
The uncertainty contained in a probability distribution is the average log-probability of an event.
翻譯過來就是,一個概率分佈所蘊含的不確定性,其實是該事件發生概率的對數均值取負數,這個概念被叫做信息熵。
\[ H(p) = - E \log (p_i) = - \sum_{i = 1}^n p_i \log(p_i) \]
假如一個地方天氣只有晴天和下雨兩種,且各自發生的概率分別是 \(p_1 = 0.3, p_2 = 0.7\),那麼我們認爲該地方天氣這一事件的信息熵是:
\[ H(p) = - (p_1\log(p_1) + p_2\log(p_2)) \approx 0.61 \]
p <- c(0.3, 0.7)
-sum(p*log(p))## [1] 0.6108643假如我們搬家到阿布扎比。那麼我們知道這裏鮮少下雨,雨天和晴天的概率可能就是 \(p_1 = 0.01, p_2 = 0.99\)。那麼在阿布扎比的天氣,其信息熵(或者簡單說叫做天氣變化的不確定性)就是約等於0.06:
p <- c(0.01, 0.99)
-sum(p*log(p))## [1] 0.056001534也就是說這裏天氣的不確定,相比一個降雨概率是30%的地方來說是相對很低的。當然,假如我們增加天氣的不同種類,例如下雪天的概率。通常信息熵會增加,也就是天氣的不確定性會增加。例如我們假設晴天,下雨,降雪的概率分別是 \(p_1 = 0.7, p_2 = 0.15, p_3 = 0.15\),那麼其天氣的信息熵就約等於0.82:
p <- c(0.7, 0.15, 0.15)
-sum(p*log(p))## [1] 0.8188084650.2.1 從信息熵到精確度 From entropy to accuracy
Divergence: The additional uncertainty induced by using probabilities from one distribution to describe another distribution.
離散度,又被叫做 Kullback-Leibler 離散度。如果某個事件的真實概率分佈 (True distribution of events) 是 \(p_1 = 0.3, p_2 = 0.7\)。如果我們使用的模型計算獲得的事後概率分佈是 \(q_1 = 0.25, q_2 = 0.75\),那麼由於模型造成的額外的不確定性 (additional uncertainty) 該如何測量呢?答案是要根據上面定義的信息熵來做比較:
\[ D_{\text{KL}} = \sum_i p_i(\log(p_i) - \log(q_i)) = \sum_i p_i \log\left( \frac{p_i}{q_i} \right) \]
也就是說,一個模型的離散程度是模型給出的概率分佈和我們希望測量的目標概率分佈之間的對數概率差的平均值 [the divergence is the average difference in log probability between the target (p) and model (q)]。這個離散度的定義其實是兩個概率分佈之間的對數概率(兩個信息熵)之差而已。
50.3 模型之間的比較
讓我們回到講解治療後偏倚部分(Chapter 49.2)時分析治療組,菌落,和植物生長之間關係的三個模型 m6.6, m6.7, m6.8。其中,m6.6 是只有截距的模型,m6.7 是預測變量同時包含菌落存在與否及治療組兩個變量的模型,m6.8 是只有治療組作爲唯一預測變量的模型。這時我們可以使用 WAIC() 命令來獲取用於比較這幾個模型的模型信息:
set.seed(71)
# number of plants
N <- 100
# simulate initial heights
h0 <- rnorm(N, 10, 2)
# assign treatments and simulate fungus and growth
treatment <- rep(0:1, each = N/2)
fungus <- rbinom( N, size = 1, prob = 0.5 - treatment * 0.4)
h1 <- h0 + rnorm( N, 5 - 3*fungus )
# compose a clean data frame
d <- data.frame( h0 = h0, h1 = h1, treatment = treatment, fungus = fungus)
# fit models m6.6-6.8 again
m6.6 <- quap(
alist(
h1 ~ dnorm(mu, sigma),
mu <- h0 * p ,
p ~ dlnorm( 0, 0.25 ),
sigma ~ dexp(1)
), data = d
)
m6.7 <- quap(
alist(
h1 ~ dnorm(mu, sigma),
mu <- h0 * p ,
p <- a + bt * treatment + bf * fungus,
a ~ dlnorm( 0, 0.2 ),
bt ~ dnorm(0, 0.5),
bf ~ dnorm(0, 0.5),
sigma ~ dexp(1)
), data = d
)
m6.8 <- quap(
alist(
h1 ~ dnorm(mu, sigma),
mu <- h0 * p,
p <- a + bt * treatment,
a ~ dlnorm(0, 0.25),
bt ~ dnorm(0, 0.5),
sigma ~ dexp(1)
), data = d
)
set.seed(11)
WAIC( m6.7 )## WAIC lppd penalty std_err
## 1 361.45112 -177.17236 3.5532002 14.170352如果能把這三個模型的信息放在一起比較就更好了:
set.seed(77)
compare( m6.6, m6.7, m6.8 , func = WAIC)## WAIC SE dWAIC dSE pWAIC weight
## m6.7 361.89010 14.261913 0.000000 NA 3.8394934 1.0000000e+00
## m6.8 402.76839 11.292507 40.878287 10.500618 2.6491648 1.3285951e-09
## m6.6 405.91739 11.661526 44.027290 12.230178 1.5828606 2.7516639e-10# compare( m6.6, m6.7, m6.8 , func = PSIS)