中心極限定理的應用
二項分佈的正態分佈近似
泊松分佈的正態分佈近似
- 假設時間 \(t\) 內某事件的發生次數服從泊松分佈 \(X\sim Po(\mu)\)。
- 考慮將這段時間 \(t\) 等分成 \(n\) 個時間段。那麼第 \(i\) 時間段內事件發生次數依舊服從泊松分佈 \(X_i\sim Po(\frac{\mu}{n})\)。且 \(E(X_i)=\mu/n, Var(X_i)=\mu/n\)。
那麼原先的 \(X\) 可以被視爲是將這無數的小時間段的 \(X_i\) 相加。應用中心極限定理： \[X=\sum_{i=1}^nX_i\sim N(\frac{n\mu}{n}, \frac{n\mu}{n})\]
需要注意的是，這段時間 (\(t\)) 內發生的事件次數 (\(\lambda\)) : \(\lambda t =\mu>10\) ，這樣的正態分佈模擬才能成立。
正態分佈模擬的校正：continuity corrections
- 如果我們使用正態分佈來模擬離散變量的分佈，常常需要用到正態分佈模擬的矯正。
- 例如：我們如果用正態分佈模擬來計算 \(P(X=15)\)，那麼實際上我們應該計算的是 \(P(14.5<X<15.5)\)。
例題
- 已知 \(X\sim Bin(100,0.5)\)，求 \(P(X>60)\)
解
\[\begin{aligned} \because X&\sim Bin(100, 0.5) \\ \therefore E(X) &=n\pi=50 \\ Var(X) &= n\pi(1-\pi) =25=5^2\\ P(X>60) &= 1-P(X\leqslant60) \\ &= 1-P(Z\leqslant\frac{60.5-50}{\sqrt{25}}) \\ &= 1-P(Z\leqslant2.1) \\ &= 1-\Phi(2.1) \\ &= 1-0.982 = 0.018 \end{aligned}\]
# 快來看實際用傻瓜算法計算獲得的概率：
1-pbinom(60, size=100, prob=0.5)## [1] 0.0176001# 快來看用中心極限定理模擬正態分佈獲得的概率：
1-pnorm((60.5-50)/sqrt(25))## [1] 0.01786442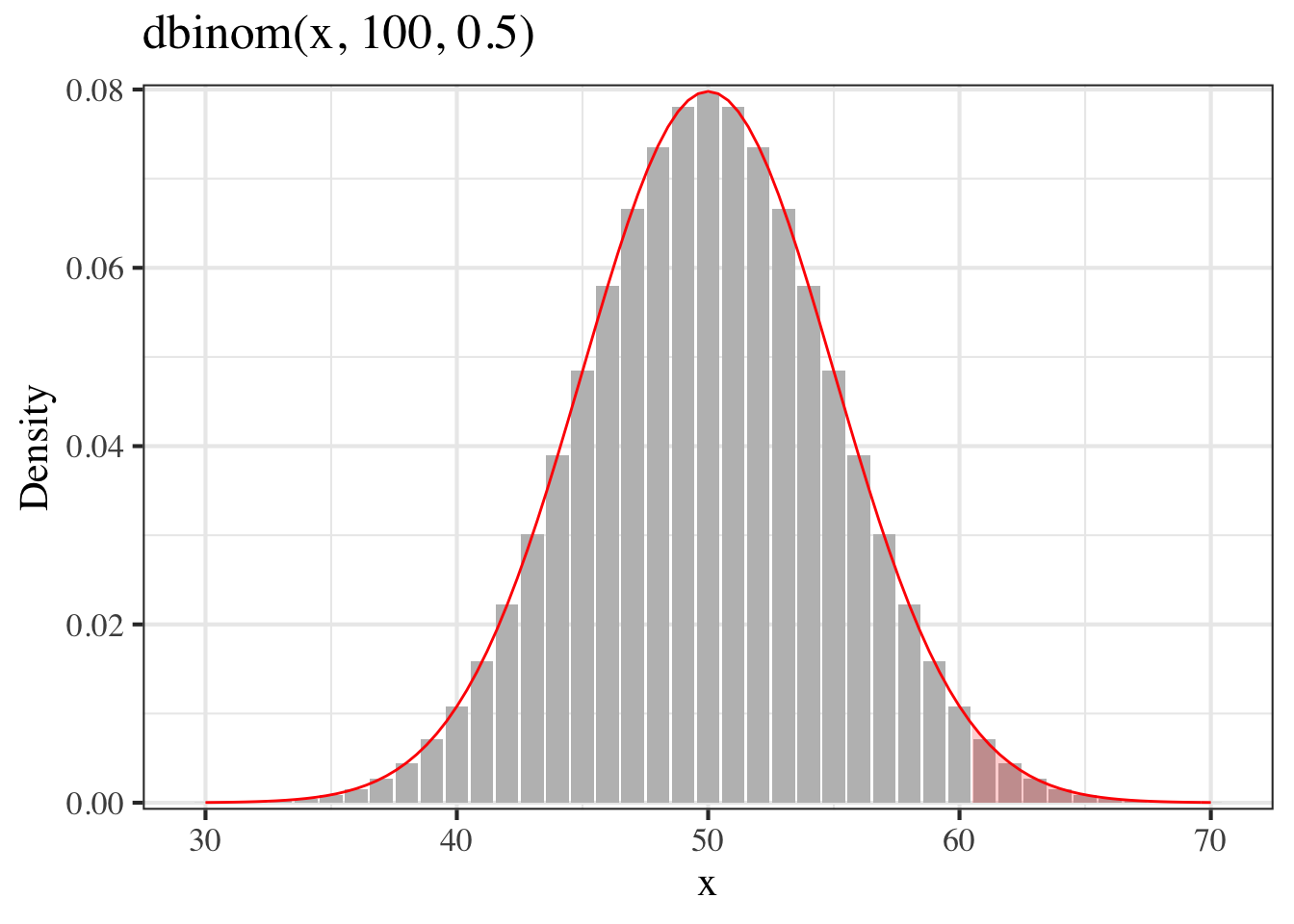
- 已知 \(X\sim Bin(48, 0.75)\), 求 \(P(30<X<39)\)
解
\[ \begin{aligned} \because B &\; \sim Bin(48, 0.75) \\ \therefore E(X) &\; =n\pi=36 \\ Var(X) &\; =n\pi(1-\pi)=9=3^2 \\ P(30<X<39) &\; = P(31\leqslant X\leqslant 38)\\ &\; = P(30.5\leqslant Y \leqslant 38.5) \\ Y\;is\;the&\;normal\;approximation \\ &\;= P(Y<38.5) - P(Y<30.5) \\ &\;= P(Z\leqslant\frac{38.5-36}{3})- P(Z\leqslant\frac{30.5-36}{3}) \\ &\;= P(Z\leqslant0.833) - P(Z\leqslant-1.833) \\ &\;= \Phi(0.833)-\Phi(-1.833) \\ &\;= 0.798-0.033 = 0.764 \end{aligned} \]
# 快來看實際用傻瓜算法計算獲得的概率：
pbinom(38, size=48, prob=0.75)-pbinom(30, size=48, prob=0.75)## [1] 0.7578159# 快來看用中心極限定理模擬正態分佈獲得的概率：
pnorm((38.5-36)/sqrt(9)) - pnorm((30.5-36)/sqrt(9))## [1] 0.7642951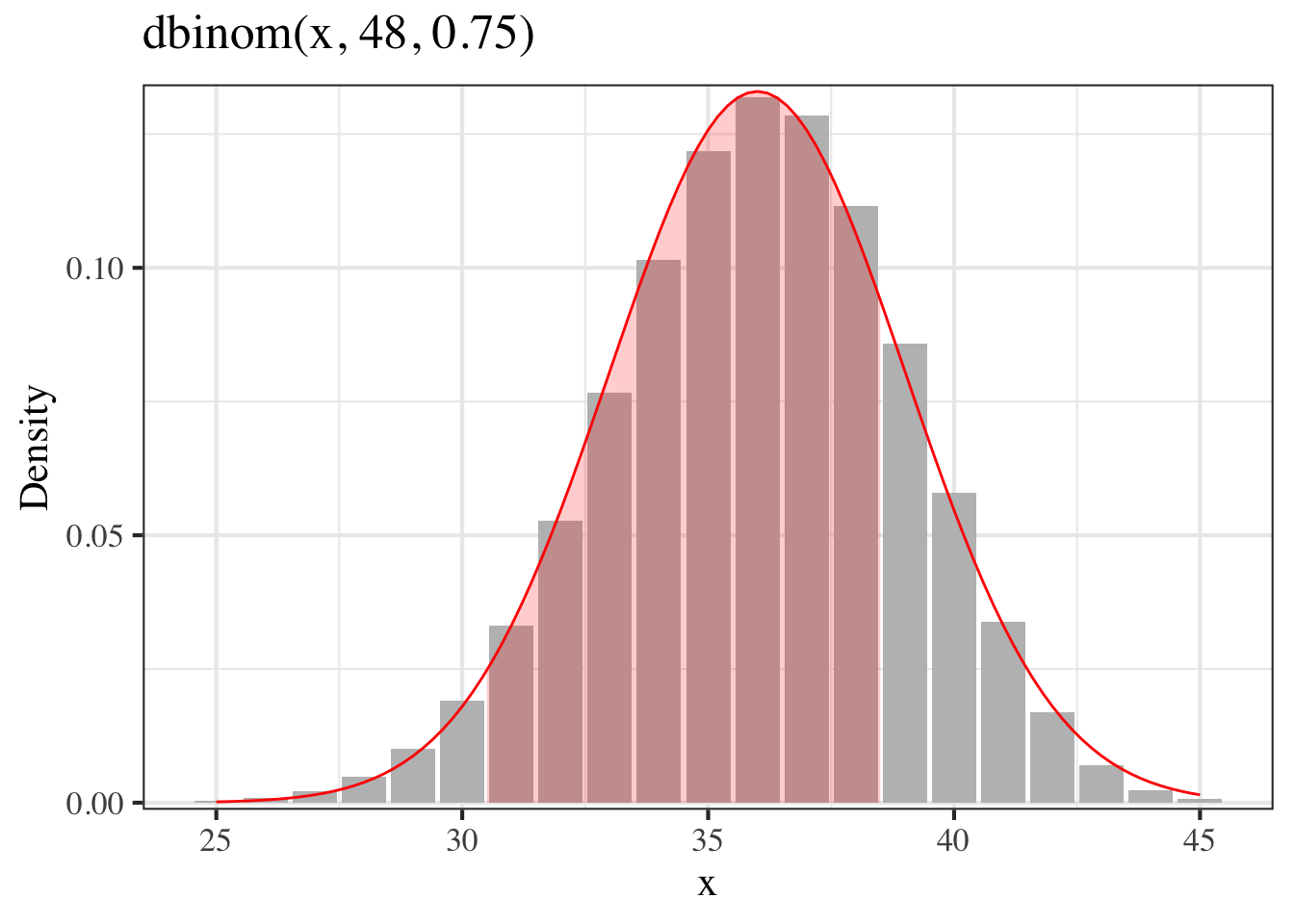
從上面兩個例題也能看出，\(n\) 越小，正態分佈模擬的誤差就越大。
- 已知 \(X \sim Poisson(30)\) 求 \(P(X\leqslant20)\)。
解
\[\because E(X)=\mu=30, \;Var(X)=\mu=30=(\sqrt{30})^2 \\ \begin{aligned} Pr(X\leqslant20) &= P(Z\leqslant\frac{20.5-30}{\sqrt{30}}) \\ &= P(Z\leqslant-1.734) \\ &= \Phi(-1.734) \\ &= 0.0414 \end{aligned} \]
# 快來看實際用傻瓜算法計算獲得的概率：
ppois(20, lambda=30)## [1] 0.03528462# 快來看用中心極限定理模擬正態分佈獲得的概率：
pnorm((20.5-30)/sqrt(30))## [1] 0.04141871這兩個其實有些小差距。不過看下圖，其模擬還是很到位的。只是正態分佈的面積明顯確實比泊松分佈的小柱子面積要大一些。
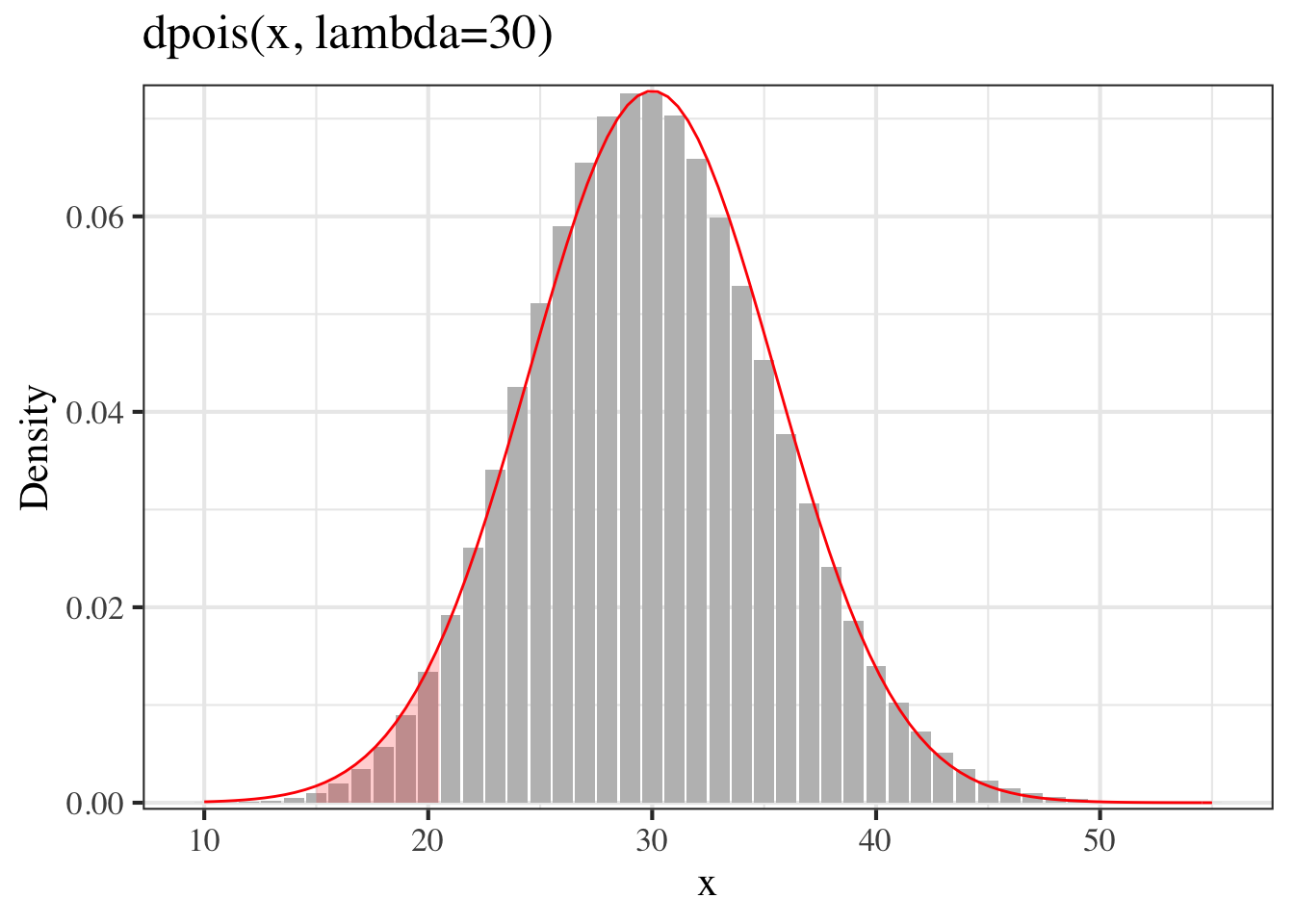
- 已知 \(X_1, X_2 \stackrel{i.i.d}{\sim} Poi(30)\) 求 \(P(X_1+X_2\leqslant40)\)。
解
\[ \begin{aligned} E(X_1+X_2) &\;= E(X_1)+E(X_2) = 30+30 = 60\\ Var(X_1+X_2) &\;= Var(X_1)+Var(X_2) = 30+30 \\ &\;= (\sqrt{60})^2 \\ P(X_1+X_2\leqslant 40) &\;= P(Z \leqslant \frac{40.5-60}{\sqrt{60}}) \\ &\;= P(Z\leqslant-2.517) \\ &\;= \Phi(-2.517) \\ &\;= 0.006 \end{aligned} \]
# 快來看實際用傻瓜算法計算獲得的概率：
ppois(40, lambda=60)## [1] 0.00398281# 快來看用中心極限定理模擬正態分佈獲得的概率：
pnorm((40.5-60)/sqrt(60))## [1] 0.005910569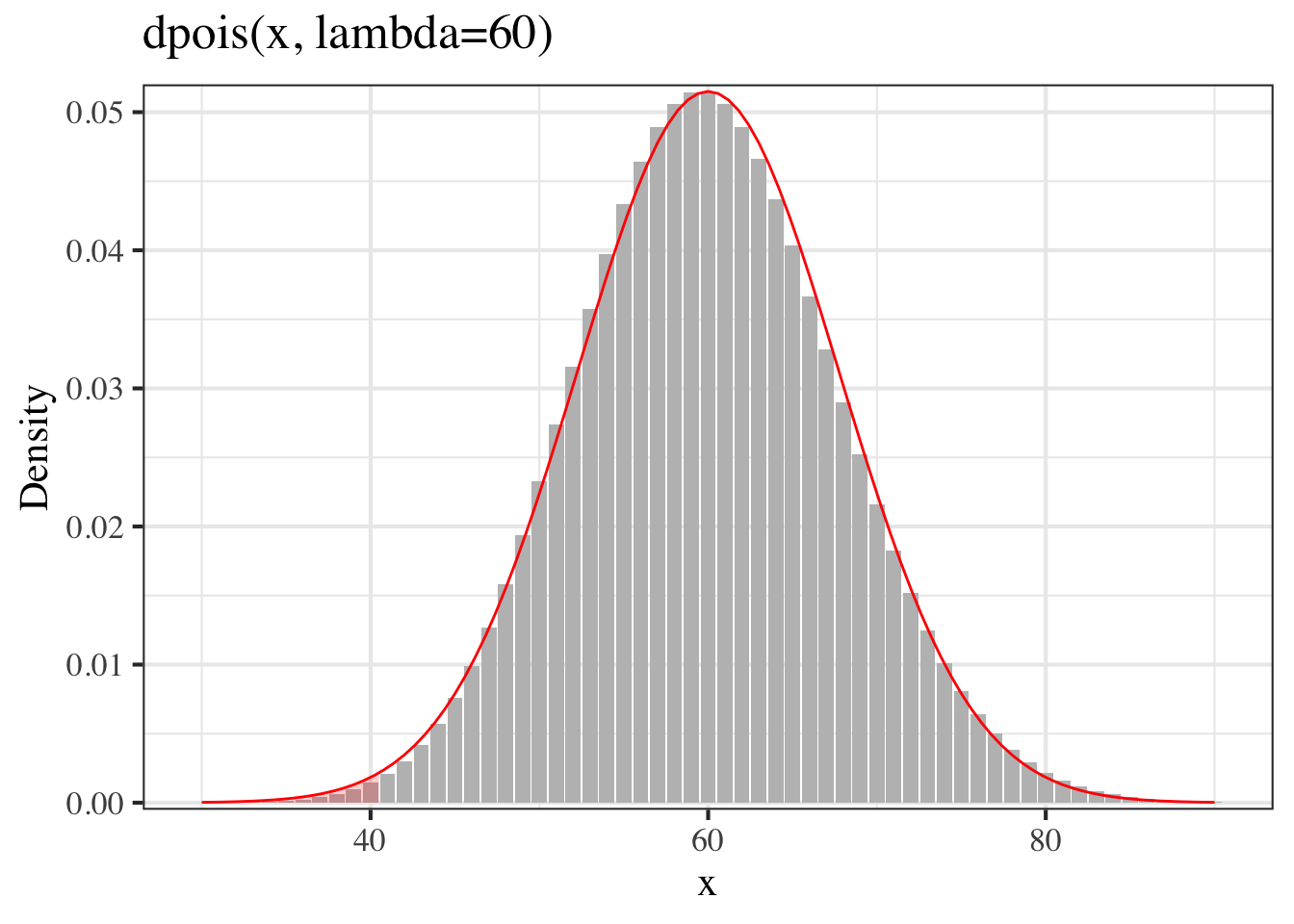
又一次，正態分佈的面積比泊松分佈的小柱子面積要大一些。
兩個連續隨機變量
假定 \(X_1, X_2\) 是兩個連續隨機變量： \[E(X_1)=\mu_1, Var(X_1)=\sigma_1^2 \\ E(X_2)=\mu_2, Var(X_2)=\sigma_2^2 \\ Corr(X_1, X_2)=\rho \Rightarrow Cov(X_1, X_2)=\rho\sigma_1\sigma_2=\sigma_{12}\]
利用矩陣的標記法，可以將 \(X_1, X_2\) 標記爲 \(\textbf{X}=(X_1, X_2)^T\), 即： \[\textbf{X}=\left( \begin{array}{c} X_1\\ X_2\\ \end{array} \right)\]
上面的所有內容都可以標記爲： \[E(\textbf{X})=\mathbf{\mu}=\left( \begin{array}{c} \mu_1\\ \mu_2\\ \end{array} \right)\\ Covariance \;matrix: \\ Var(\textbf{X})=\mathbf{\Sigma}=\left( \begin{array}{c} \sigma_1^2 & \sigma_{12}\\ \sigma_{12} & \sigma_1^2\\ \end{array} \right)\]
兩個連續隨機變量 例子：
假如要看收縮期血壓 (\(SBP\)) 和舒張期血壓 (\(DBP\)) 之間的關係：
下列爲已知條件：
- \(SBP\) 的均值爲 \(130\)， 標準差爲 \(15\);
- \(DBP\) 的均值爲 \(90\), 標準差爲 \(10\);
- \(SBP\) 和 \(DBP\) 之間的相關係數爲 \(0.75\)。
那麼， 我們可以把這些信息用下面的方法來標記：
\[E(\textbf{X})=\mathbf{\mu}=\left( \begin{array}{c} 130\\ 90\\ \end{array} \right)\\ Var(\textbf{X})=\mathbf{\Sigma}=\left( \begin{array}{c} 225 & 112.5\\ 112.5 & 225\\ \end{array} \right)\]
條件分佈和邊緣分佈的概念
- 如果 \(\textbf{X}=(X_1, X_2)^T\) 的兩個變量都服從正態分佈；
那麼這兩個變量的邊緣分佈 (marginal distribution) 也服從正態分佈: \[X_1\sim N(\mu_1,\sigma_1^2), X_2\sim N(\mu, \sigma_2^2)\]
- 同樣的，\(X_1\) 的給出 \(X_2\) 的條件分佈 (condition distribution) 也服從正態分佈： \[E(X_1|X_2)=\mu_1+\frac{\rho\sigma_1}{\sigma_2}(X_2-\mu_2) \\ Var(X_1|X_2)=\sigma_1^2(1-\rho^2)\]
反之亦然。
條件分佈和邊緣分佈的例子
上面的概念過於抽象，用血壓的例子：
收縮期血壓和舒張期血壓各自服從正態分佈。那麼可以用上面的概念來寫出已知舒張期血壓時，收縮期血壓的分佈。
條件期望: \[E(SBP|DBP)=130+\frac{0.75\times15}{10}(DBP-90)\]
實際如果來了一個病人，他說他只記得自己測的舒張期血壓是95：
他的收縮期血壓的期望值就可以用上面的式子計算： \[E(SBP|DBP=95)=136\]條件方差爲： \[Var(SBP|DBP)=15^2(1-0.75^2)=98.4\approx9.92^2<15^2\]
所以當我們知道了這個人的一部分信息以後，推測他的另一個相關連的變量變得更加準確(方差變小)了。
例題
有 (閒) 人記錄了 \(1494\) 名兒童在 \(2, 4, 6\) 歲時的腿長度。已知在記錄的這三個年齡時的平均腿長度分別爲 \(85 cm, 103cm, 114cm\)。協方差矩陣如下:
\[\left( \begin{array}{c} 22.2 & 11.8 & 13.7\\ 11.8 & 26.3 & 21.5\\ 13.7 & 21.5 & 29.0 \end{array} \right)\]
假定，這三個年齡記錄的這些兒童的腿長度數據（聯合分佈, joint distribution）服從三個變量正態分佈。
- 求 \(2\) 歲時這些兒童的腿長度的邊緣分佈 (marginal distribution)
解
\[X_{age=2} \sim N(85, \sigma_{age=2}^2=22.2)\]
- 求他們 \(6\) 歲時腿長度的 \(2\) 歲時的條件分佈。(Find the distribution of leg length age 6 conditional on leg length at age 2.)
解
\(6\) 歲時和 \(2\) 歲時腿長的相關係數 (correlation, \(\rho_{6,2}\)) 爲： \[ \begin{aligned} \rho_{6,2} &= \frac{Cov_{6,2}}{\sqrt{Var(length_6)}\sqrt{Var(length_2)}}\\ &= \frac{13.7}{\sqrt{22.2}\sqrt{29}}=0.54 \end{aligned} \]
條件分佈套用上面提到的公式：
\[ \begin{aligned} E(length_6 | length_2) &= \mu_6+\frac{\rho_{6,2}\sigma_6}{\sigma_2}(length_2-\mu_2) \\ &= 114+\frac{0.54\times\sqrt{29.0}}{\sqrt{22.2}}(length_2-85)\\ Var(length_6 | length_2) &= \sigma_6^2(1-\rho_{6,2}^2) \\ &= 29.0\times(1-0.54^2) =20.5 \end{aligned} \]
)