概率論2
Bayes 理論的概念
許多時候,我們需要將概率中的條件相互對調。 例如: 在已知該人羣中有20%的人有吸菸習慣(\(P(S)\)),吸菸的人有9%的概率有哮喘(\(P(A|S)\)),不吸菸的人有7%的概率有哮喘(\(P(A|\bar{S})\))的前提下,有個人前來門診,發現是哮喘患者,那麼這個人有多大的概率是一個菸民?也就是要求 \(P(S|A)\)
這裏先引入貝葉斯的概念:
我們可以將 \(P(A\cap S)\) 寫成: \[P(A\cap S)=P(A|S)P(S)\\or\\ P(A\cap S)=P(S|A)P(A)\] 這兩個等式是完全等價的。我們將他們連起來:
\[P(S|A)P(A)=P(A|S)P(S)\\ \Rightarrow P(S|A)=\frac{P(A|S)P(S)}{P(A)}\]
是不是看起來又像是寫了一堆廢話? 沒錯,你看出來是一堆廢話的時候,證明你也同意這背後的簡單邏輯。
再繼續,我們可以利用另外一個廢話:\(\because S+\bar{S}=1\\ \therefore P(A)=P(A\cap S)+P(A\cap\bar{S})\)
用上面的公式替換掉 \(P(A\cap S)+P(A\cap\bar{S}) \\ \therefore P(A)=P(A|S)P(S)+P(A|\bar{S})P(\bar{S})\)
可以得到貝葉斯理論公式:
\[P(S|A)=\frac{P(A|S)P(S)}{P(A|S)P(S)+P(A|\bar{S})P(\bar{S})}\]
回到上面說到的哮喘人中有多少比例吸菸的問題。可以繼續使用概率樹來方便的計算:
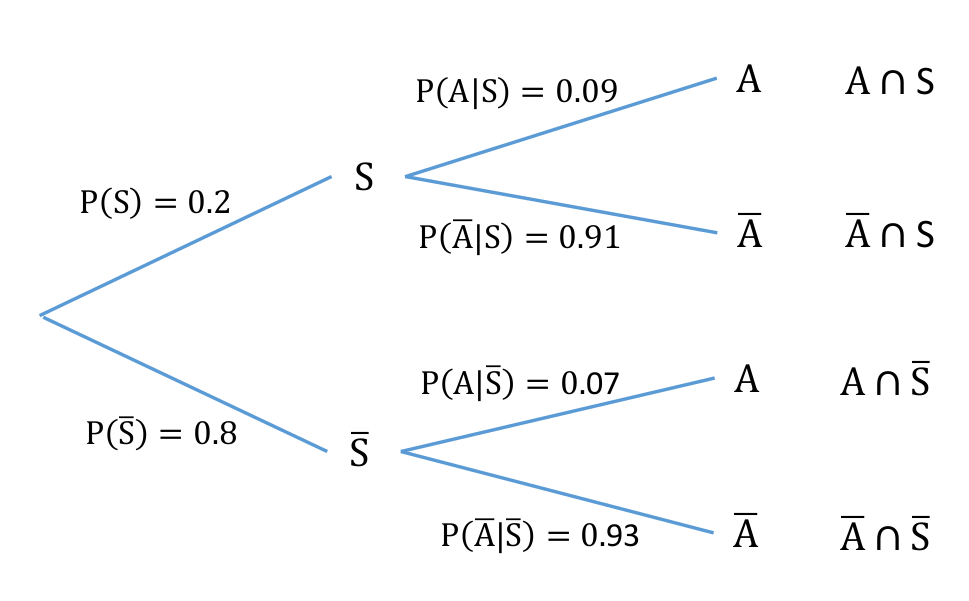
\[\begin{align} P(S|A) &= \frac{P(A|S)P(S)}{P(A|S)P(S)+P(A|\bar{S})P(\bar{S})} \\ &= \frac{0.09\times0.2}{0.09\times0.2+0.07\times0.8} \\ &= 0.24 \end{align}\]
所以我們的結論就是,在已知該人羣中有20%的人有吸菸習慣(\(P(S)\)),吸菸的人有9%的概率有哮喘(\(P(A|S)\)),不吸菸的人有7%的概率有哮喘(\(P(A|\bar{S})\))的前提下,有個人前來門診,發現是哮喘患者,那麼這個人有24% 的概率是一個菸民(\(P(S|A)\))。
期望 Expectation (或均值 or mean) 和 方差 Variance
期望(或均值)是用來描述一組數據中心位置的指標(另一個是中位數 Median)。 對於離散型隨機變量 \(X\) (discrete random variables),它的期望被定義爲:
\[E(X)=\sum_x xP(X=x)\]
所以就是將所有 \(X\) 可能取到的值乘以相應的概率後求和。這個期望(或均值)常常用希臘字母 \(\mu\) 來標記。
方差 Variance 是衡量一組數據變化幅度(dispersion/variability)的指標之一。 方差的定義是:
\[Var(X)=E((X-\mu)^2)\\其中,\mu=E(x)\]
實際上我們更加常用的是它的另外一個公式:
\[Var(X)=E(X^2)-E(X)^2\]
證明 上面兩個方差公式相等
\[\begin{align} Var(x) &= E((X-\mu)^2) \\ &= E(X^2-2X\mu+\mu^2)\\ &= E(X^2) - 2\mu E(X) + \mu^2\\ &= E(X^2) - 2\mu^2 + \mu^2 \\ &= E(X^2) - \mu^2 \\ &= E(X^2) - E(X)^2 \end{align}\]
方差的性質:
- \(Var(X+b)=Var(X)\)
- \(Var(aX)=a^2Var(X)\)
- \(Var(aX+b)=a^2Var(X)\)
伯努利分佈 Bernoulli distribution
伯努利分佈,說的就是一個簡單的二分變量 (1, 0),它取1時的概率如果是 \(\pi\)。那麼我們可以計算這個分佈的期望值:
\[\begin{align} E(X) &=\sum_x xP(X=x) \\ &=1\times\pi + 0\times(1-\pi)\\ &=\pi \end{align}\]
由於 \(x=x^2\),因爲 \(x=0,1\), 所以 \(E[X^2]=E[X]\),那麼方差爲:
\[\begin{align} Var(X) &=E[X^2]-E[X]^2 \\ &=E[X]-E[X]^2 \\ &=\pi - \pi^2 \\ &=\pi(1-\pi) \end{align}\]
證明,\(X,Y\) 爲互爲獨立的隨機離散變量時,
a) \(E(XY)=E(X)E(Y)\) ;
b) \(Var(X+Y)=Var(X)+Var(Y)\)
- 證明
\[\begin{align} E(XY) &= \sum_x\sum_y xyP(X=x, Y=y) \\ \because &\; X,Y are\;independent\;to\;each\;other \\ \therefore &= \sum_x\sum_y xyP(X=x)P(Y=y)\\ &=\sum_x xP(X=x)\sum_y yP(Y=y)\\ &=E(X)E(Y) \end{align}\]
- 證明 根據方差的定義: \[\begin{align} Var(X+Y) &= E((X+Y)^2)-E(X+Y)^2 \\ & \; Expand \\ &=E(X^2+2XY+Y^2)-(E(X)+E(Y))^2\\ &=E(X^2)+E(Y^2)+2E(XY)\\ &\;\;\; - E(X)^2-E(Y)^2-2E(X)E(Y)\\ &\; We\;just\;showed\; E(XY)=E(X)E(Y)\\ &=E(X^2)-E(X)^2+E(Y^2)-E(Y)^2 \\ &=Var(X)+Var(Y) \end{align}\]