二次方程近似法求對數似然比 approximate log-likelihood ratios
爲什麼要用二次方程近似對數似然比方程?
- 上節也看到,我們會碰上難以用代數學計算獲得對數似然比信賴區間的情況 (binomial example)。
- 我們同時知道,對數似然比方程會隨着樣本量增加而越來越漸進於二次方程,且左右對稱。
- 所以,我們考慮當樣本量足夠大時,用二次方程來近似對數似然比方程從而獲得參數估計的信賴區間。
正態近似法求對數似然 Normal approximation to the log-likelihood
根據前一節,如果樣本均數的分佈符合正態分佈:\(\bar{X}\sim N(\mu, \sigma^2/n)\)。那麼樣本均數的對數似然比爲:
\[llr(\mu|\bar{X})=\ell(\mu|\bar{X})=-\frac{1}{2}(\frac{\bar{x}-\mu}{\sigma/\sqrt{n}})^2\]
其中, \(\bar{x}\) 是正態分佈總體均數 \(\mu\) 的極大似然估計 (maximum likelihood estimator, MLE)。如果已知總體的方差參數,那麼 \(\sigma/\sqrt{n}\) 是 \(\bar{x}\) 的標準誤 (standard error)。
因此,假設 \(\theta\) 是我們想尋找的總體參數。有些人提議可以使用下面的關於 \(\theta\) 的二次方程來做近似:
\[f(\theta|data)=-\frac{1}{2}(\frac{\theta-M}{S})^2\]
上述方程具有一個正態二次對數似然 (比) 的形式,而且該方程的極大似然估計(MLE), \(M\) 的標準誤爲 \(S\)。如果我們正確地選用 \(M\) 和 \(S\),那我們就可以用這樣的方程來近似求真實觀察數據的似然 \(\ell(\theta|data)\)。
通過近似正態對數似然比,\(M\) 應當選用使方程取最大值時,參數 \(\theta\) 的極大似然估計 \(M=\hat{\Theta}\)。
但是在選用標準誤 \(S\) 上必須滿足下列條件:
- \(S\) 是極大似然估計 \(\hat{\Theta}\) 的標準誤。
- 被選擇的 \(S\) 必須儘可能的使該二次方程形成一個十分接近真實的對數似然比方程。特別是在最大值的部分必須與之無限接近或者一致。所以二者在 MLE 的位置應當有相同的曲率(二階導數)。
由於,一個方程的曲率是該方程的二階導數(斜線斜率變化的速度)。所以對數似然比方程在 MLE 取最大值時的曲率(二階導數)爲:
\[\left.\frac{d^2}{d\theta^2}\ell(\theta)\right\vert_{\theta=\hat{\theta}}=\ell^{\prime\prime}(\hat{\theta})=-\frac{1}{S^2}\\ \Rightarrow S^2=\left.-\frac{1}{\ell^{\prime\prime}(\theta)}\right\vert_{\theta=\hat{\theta}} \]
在正態分佈的例子下,\(M=\bar{x}, S=\sigma/\sqrt{n}\)。對數似然比方程最大值時的曲率(二階導數)恰好就爲標準誤的平方的負倒數:
\(\ell^{\prime\prime}(\theta)=-\frac{1}{SE^2}\) \(\Rightarrow\) 被叫做 Fisher information。
稍微總結一下:
- 任意的對數似然比方程 \(llr(\theta)\) 都可以考慮用一個二次方程來近似: \[f(\theta|data)=-\frac{1}{2}(\frac{\theta-M}{S})^2\]
- 其中
\(\begin{aligned} &M=\hat\theta\\ &S^2=\left.-\frac{1}{\ell^{\prime\prime}(\theta)}\right\vert_{\theta=\hat{\theta}}\\ &when \\ & n\rightarrow\infty \Rightarrow \begin{cases} S^2\rightarrow Var(\hat\theta) \\ S\rightarrow SE(\hat\theta) \end{cases} \end{aligned}\)
近似法估算對數似然比的信賴區間
一旦我們決定了使用正態近似法來模擬對數似然比方程,對數似然比的信賴區間算法就回到了前一節中我們算過的方法,也就是:
\[-2f(\theta)<\mathcal{X}_{1,(1-\alpha)}^2\]
故信賴區間爲: \(m\pm\sqrt{\mathcal{X}_{1,(1-\alpha)}^2}S\)。求\(95\%\) 水平的信賴區間時,\(\mathcal{X}_{1,0.95}^2=3.84\),所以就又看到了熟悉的 \(M\pm1.96S\)。
以泊松分佈爲例
一個被追蹤的樣本,經過了 \(p\) 人年的觀察,記錄到了 \(d\) 個我們要研究的事件:
\[D\sim Poi(\mu), where \mu=\lambda p\]
Step 1. 找極大似然估計 (MLE),之前介紹似然方程時推導過的泊松分佈的似然方程:
\[\begin{aligned} P(D=d|\lambda) &= \frac{e^{-\mu}\cdot\mu^d}{d!} \\ &=\frac{e^{-\lambda p}\cdot\lambda^d p^d}{d!} \\ omitting&\;terms\;not\;in\;\mu \\ &\Rightarrow \ell(\lambda) = dlog\lambda - \lambda p \\ &\Rightarrow \ell^\prime(\lambda) = \frac{d}{\lambda} -p \\ &\Rightarrow \hat\lambda=\frac{d}{p} = \textbf{M} \end{aligned}\]
Step 2. 求似然方程的二階導數,確認 MLE 是使方程獲得最大值的點,然後確定 \(S^2\):
\[\begin{aligned} & \ell^\prime(\lambda) = \frac{d}{\lambda} -p \\ & \Rightarrow \ell^{\prime\prime}(\lambda) = -\frac{d}{\lambda^2}<0 \Rightarrow \textbf{MLE is maximum} \\ & S^2 = \left.-\frac{1}{\ell^{\prime\prime}(\lambda)}\right\vert_{\lambda=\hat{\lambda}=d/p} = -\frac{1}{-d/\hat\lambda^2} = -\frac{1}{-d/(d/p)^2} \\ &\Rightarrow S^2 = \frac{d}{p^2} \\ \end{aligned}\]
Step 3. 把前兩部求得的 \(MLE\) 和 \(S^2\) 代入近似的二次方程:
\[\begin{aligned} & \hat\lambda=\frac{d}{p}=M,\; S^2 = \frac{d}{p^2} \\ & using\;approximate\;quadratic\;llr \\ & q(\lambda) = -\frac{1}{2}(\frac{\lambda-M}{S})^2\\ &\Rightarrow q(\lambda) = -\frac{1}{2}(\frac{\lambda-\frac{d}{p}}{\frac{\sqrt{d}}{p}})^2\\ & let \; q(\lambda)=-1.92\\ &\Rightarrow -\frac{1}{2}(\frac{\lambda-\frac{d}{p}}{\frac{\sqrt{d}}{p}})^2=-1.92\\ &(\frac{\lambda-\frac{d}{p}}{\frac{\sqrt{d}}{p}})^2=3.84\\ &\frac{\lambda-\frac{d}{p}}{\frac{\sqrt{d}}{p}} = \pm1.96\\ &\Rightarrow 95\%CI \;for \;\lambda = \frac{d}{p}\pm1.96\frac{\sqrt{d}}{p} \end{aligned}\]
結論就是: 發病(死亡)率 \(\lambda\) 的 \(95\%\) 信賴區間爲: \(M\pm1.96S\)。所以我們不需要每次都代入對數似然比方程,只要算出 \(MLE = M\) 和 \(S\) 之後代入這個公式就可以用二次方程近似法算出信賴區間。
以二項分佈爲例
\[K\sim Bin(n,\pi)\]
Step 1. 找極大似然估計 (MLE):
\[ \begin{aligned} & Prob(K=k) = \pi^k(1-\pi)\binom{n}{k}\\ &\Rightarrow L(\pi|k) = \pi^k(1-\pi)\binom{n}{k}\\ &omitting\;terms\;not\;in\;\pi \\ &\Rightarrow \ell(\pi) = k\:log\pi+(n-k)log(1-\pi) \\ &\ell^\prime(\pi) = \frac{k}{\pi}-\frac{n-k}{1-\pi} \\ & let\;\ell^\prime(\hat\pi) =0 \\ &\Rightarrow \frac{k}{\hat\pi}-\frac{n-k}{1-\hat\pi}=0\\ &\Rightarrow \frac{\hat\pi}{1-\hat\pi}=\frac{k}{n-k}\\ &\Rightarrow \frac{\hat\pi}{1-\hat\pi}=\frac{k/n}{1-k/n}\\ &\Rightarrow \hat\pi=\frac{k}{n} = p = \textbf{M} \end{aligned} \]
Step 2. 將對數似然方程的二次微分 (二階導數),確認在 MLE 爲極大值,並確認 \(S^2\):
\[ \begin{aligned} &\ell^\prime(\pi) = \frac{k}{\pi}-\frac{n-k}{1-\pi} \\ &\ell^{\prime\prime}(\pi)=\frac{-k}{\pi^2}-\frac{n-k}{(1-\pi)^2} <0 \\ &\therefore at\;\textbf{MLE}\;\ell(\pi)\;has\;maximum \\ S^2&=\left.-\frac{1}{\ell^{\prime\prime}(\pi)}\right\vert_{\pi=\hat\pi=k/n=p}\\ &=\frac{1}{\frac{k}{\hat\pi^2}+\frac{n-k}{(1-\hat\pi)^2}}\\ &=\frac{\hat\pi^2(1-\hat\pi)^2}{k(1-\hat\pi)^2+(n-k)\hat\pi^2}\\ &=\frac{P^2(1-P)^2}{np(1-p)^2+(n-np)p^2}\\ &=\frac{p(1-p)}{n(1-p)+np}\\ &=\frac{p(1-p)}{n}\\ &\Rightarrow S=\sqrt{\frac{p(1-p)}{n}} \end{aligned} \]
Step 3. 將求得的 MLE 和 \(S^2\) 代入近似信賴區間:
\[ 95\% CI \;for \; \pi:\\ M\pm1.96S=p\pm1.96\sqrt{\frac{p(1-p)}{n}}\\ \]
參數轉化 parameter transformations
如果將參數 \(\theta\) 通過某種數學方程轉化成 \(g(\theta)\),那麼我們可以認爲,轉化後的方程的 MLE 爲 \(g(\hat\theta)\),其中 \(\hat\theta\) 是參數 \(\theta\) 的 MLE。
類似地,如果 \(\theta_1 \sim \theta_2\) 是參數 \(\theta\) 的似然比信賴區間,那麼 \(g(\theta_1)\sim g(\theta_2)\) 就是 \(g(\theta)\) 的似然比信賴區間。
以下爲轉換參數以後獲取信賴區間的步驟:
- 將參數通過某些數學方程(通常是取對數)轉化,使新的對數似然比方程更加接近二次方程的對稱圖形。
Transform parameter so that \(llr\) is closer to a quadratic shape. - 用本節學到的二次方程近似法,求得轉化後的參數的似然比信賴區間。
Use our quadratic approximation on the transformed parameter to calculate our likelihood ratio confidence intervals. - 將第2步計算獲得的似然比信賴區間再通過轉化參數時的逆函數轉換回去,以獲得原參數的似然比信賴區間。
Transform the confidence intervals back, or to any scale we wish – they remain valid.
以泊松分佈爲例
當我們用泊松分佈模擬事件在某段時間內發生率 \(\lambda\) 時,注意到這個事件發生率必須滿足 \(\lambda>0\)。當事件發生次數較低時,會讓似然方程的圖形被擠壓在低值附近。如果嘗試用對數轉換 \(\lambda \rightarrow log(\lambda)\) 此時 \(log(\lambda)\) 就不再被限制與 \(>0\)。下面我們嘗試尋找對數轉換過後的 \(M\) 和 \(S\)。
令 \(\beta=log(\lambda), \Rightarrow e^\beta=\lambda\) 從本文上半部分中我們已知 \(\hat\lambda=\frac{d}{p}\)。
- 對數轉換以後的 \(M\) 是什麼?
根據定義,\(MLE(\beta)=MLE[log(\lambda)]=log(\hat\lambda)\) \(\Rightarrow M=\hat\beta=log(\frac{d}{p})\) 對數轉換以後的 \(S\) 是什麼?
\(\begin{aligned} & \ell(\beta|d)=d \beta - pe^\beta\\ & \Rightarrow \ell^\prime(\beta)=d-pe^\beta \Rightarrow \ell^{\prime\prime}(\beta)=-pe^\beta \\ & S^2 = \left.-\frac{1}{\ell^{\prime\prime}(\beta)}\right\vert_{\beta=\hat{\beta}} = \left.\frac{1}{pe^\beta}\right\vert_{\beta=\hat{\beta}} = \frac{1}{pe^{log(d/p)}}\\ &\Rightarrow S^2=\frac{1}{d} \therefore S=\frac{1}{\sqrt{d}} \end{aligned}\)
泊松分佈的對數似然方程是:\(\ell(\lambda|d)=d log(\lambda) - \lambda p\) 用 \(\beta\) 替換掉 \(\lambda\)轉換後的近似二次方程:
\(\begin{aligned} & q(\beta) = -\frac{1}{2}(\frac{\beta-M}{S})^2 = -\frac{1}{2}(\frac{\beta-log(\frac{d}{p})}{\frac{1}{\sqrt{d}}})^2 \end{aligned}\)\(\beta\) 的 \(95\%\) 信賴區間 \(=log(\frac{d}{p})\pm1.96\frac{1}{\sqrt{d}}\)
\(\lambda\) 的 \(95\%\) 信賴區間 \(=exp(log(\frac{d}{p})\pm1.96\frac{1}{\sqrt{d}})\)
以二項分佈爲例
在研究對象 \(n\) 人中觀察到 \(k\) 個人患有某種疾病。
令 \(\beta=log(\pi) \Rightarrow \pi=e^\beta\) 從上文的推倒也已知 \(\hat\pi=\frac{k}{n}=p\)
\(\begin{aligned} &\Rightarrow \ell(\beta)=klog\pi+(n-k)log(1-\pi)=k\beta+(n-k)log(1-e^\beta) \\ &\Rightarrow \ell^{\prime}(\beta)=k-\frac{(n-k)(e^\beta)}{1-e^\beta} \\ &\Rightarrow \ell^{\prime\prime}(\beta)=-(n-k)\frac{e^\beta(1-e^\beta)+e^{2\beta}}{(1-e^\beta)^2} \\ & \ell^{\prime\prime}(\beta)= -(n-k)\frac{e^\beta}{(1-e^\beta)^2}\\ &\Rightarrow S^2 = \left.-\frac{1}{\ell^{\prime\prime}(\beta)}\right\vert_{\beta=\hat{\beta}} = \frac{(1-e^{\hat\beta})^2}{(n-k)e^{\hat\beta}} \\ &\because \hat\beta=log(\hat\pi) \\ &\therefore e^{\hat\beta} = \frac{k}{n}\\ &\Rightarrow S^2=\frac{(1-\frac{k}{n})^2}{(n-k)\frac{k}{n}}=\frac{n-k}{nk}=\frac{1}{k}-\frac{1}{n}\\ & \Rightarrow S=\sqrt{\frac{1}{k}-\frac{1}{n}}\\ \end{aligned}\)
Exercise
Q1
- 在\(n=100\)人中觀察到有\(k=40\)人患病,假設每個人只有患病,不患病兩個狀態,用二項分佈來模擬這個數據,\(\pi\) 爲患病的概率。下面是 \(\pi \in [0.2,0.6]\) 區間的對數似然比方程曲線。
pi <- seq(0.2, 0.6, by=0.01)
L <- (pi^40)*((1-pi)^60)
Lmax <- rep(max(L), 41)
LR <- L/Lmax
logLR <- log(LR)
plot(pi, logLR, type = "l", ylim = c(-11, 0),yaxt="n",
frame.plot = FALSE, ylab = "logLR(\U03C0)", xlab = "\U03C0")
grid(NA, 5, lwd = 2) # add some horizontal grid on the background
axis(2, at=seq(-12,0,2), las=2)
title(main = "Figure 1. Binomial log-likelihood ratio")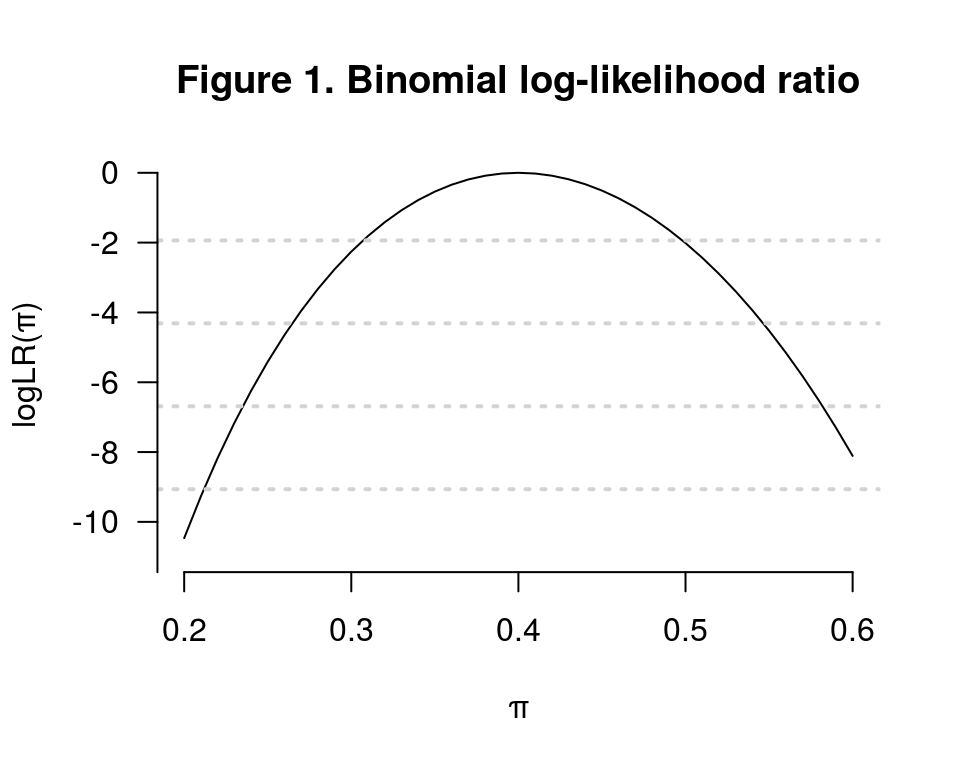
- 用一個二次方程來模擬上面的對數似然比曲線:\(f(\pi)=-\frac{(\pi-M)^2}{2S^2}\),其中 \(M=\hat\pi=\frac{k}{n}=0.4\),\(S^2=\frac{p(1-p)}{n}=0.0024\)
par(mai = c(1.2, 0.5, 1, 0.7))
quad <- -(pi-0.4)^2/(2*0.0024)
plot(pi, quad, type = "l", ylim = c(-4, 0),yaxt="n", col="red",
frame.plot = FALSE, ylab = "", xlab = "\U03C0")
lines(pi, logLR, col="black")
grid(NA, 4, lwd = 1) # add some horizontal grid on the background
axis(2, at=seq(-4,0,1), las=2)
title(main = "Figure 2. Quadratic approximation\n of binomial log-likelihood ratio \n 40 out of 100 subjects")
abline(h=-1.92, lty=1, col="red")
axis(4, at=-1.92, las=2)
legend(x=0.27, y= -5.5 ,xpd = TRUE, legend=c("logLR","Quadratic"), bty = "n",
col=c("black","red"), lty=c(1,1), horiz = TRUE) #the legend is below the graph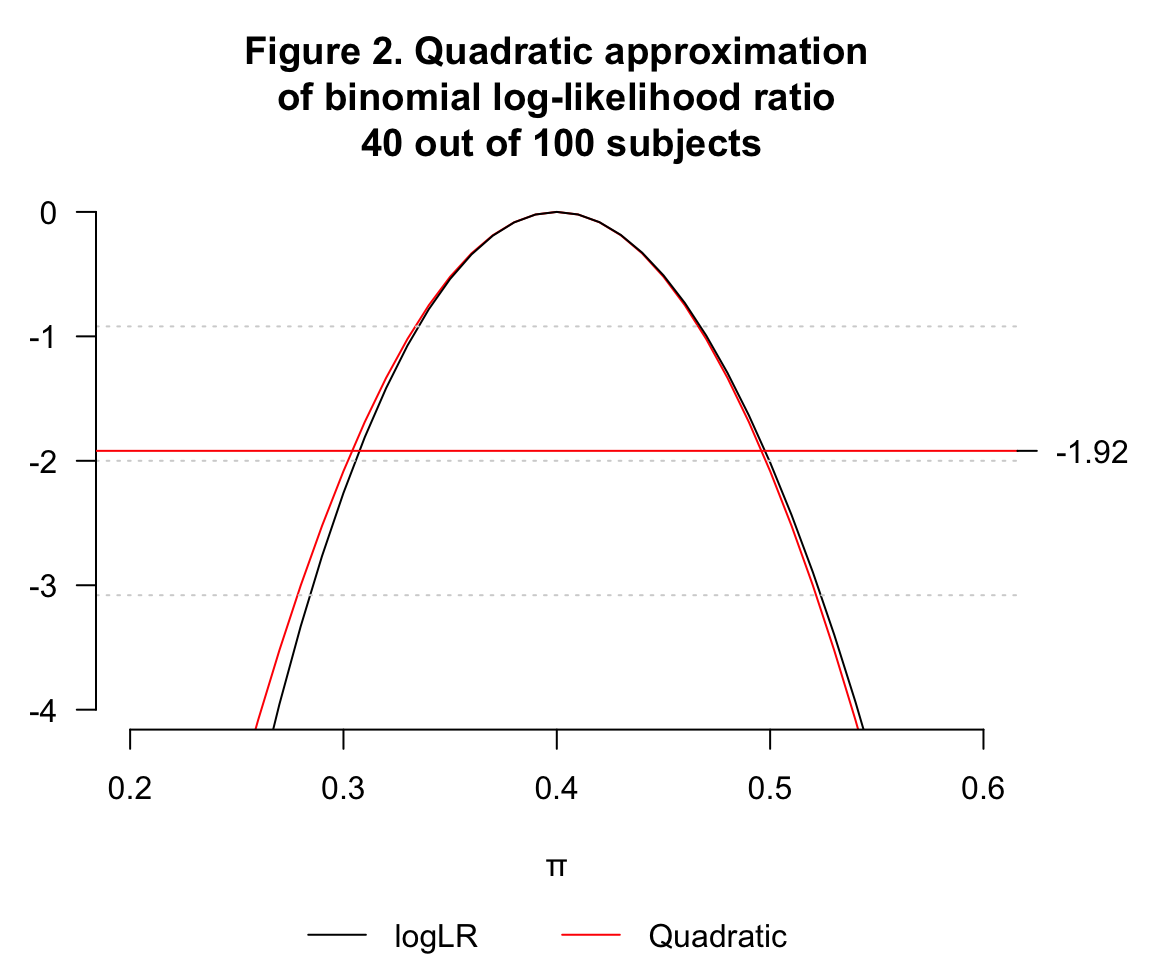
Q2
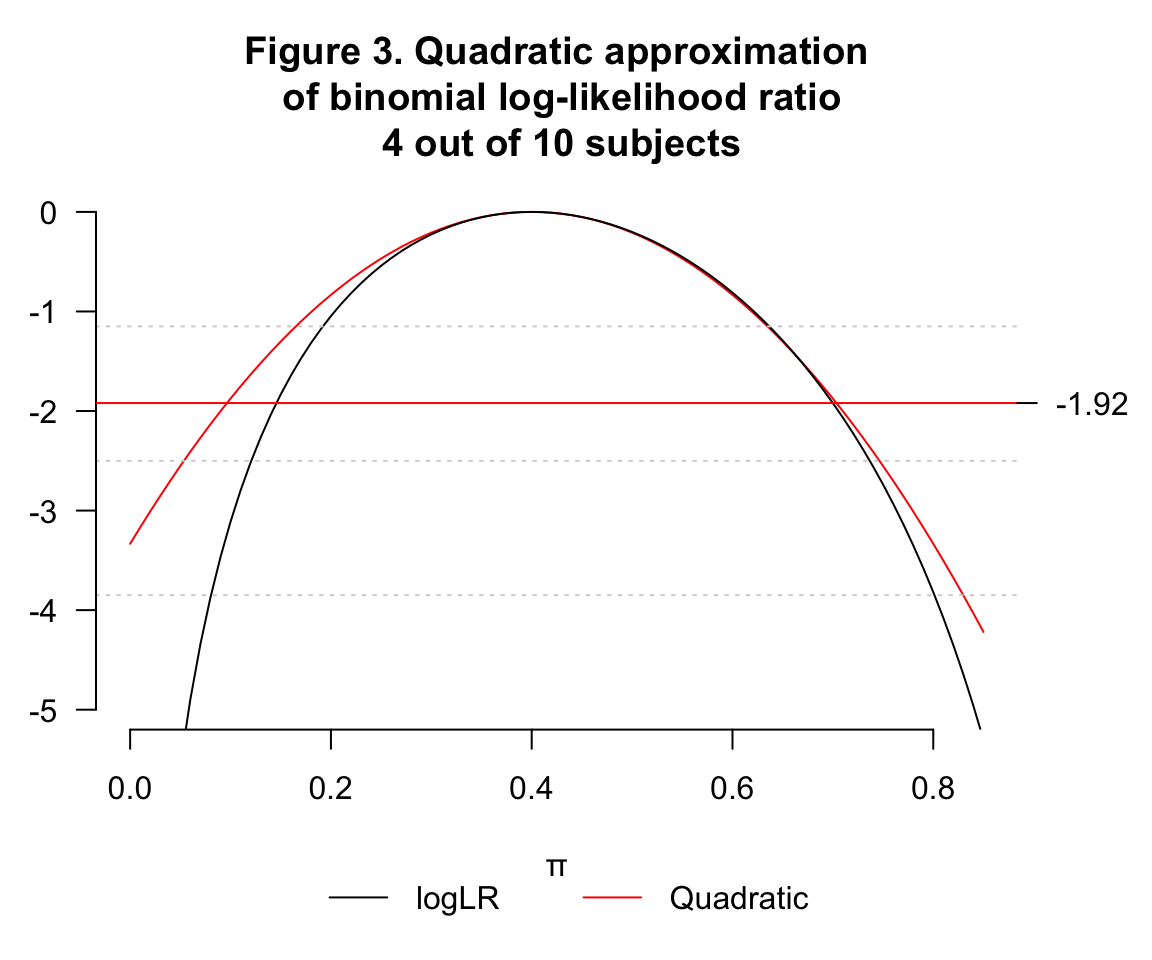
依舊使用二項分佈數據來模擬,觀察不同的事件數量和樣本量對近似計算的影響。
- 類比上面的問題,用同樣的 \(\hat\pi=0.4\),但是 \(n=10, k=4\) 時的圖形:
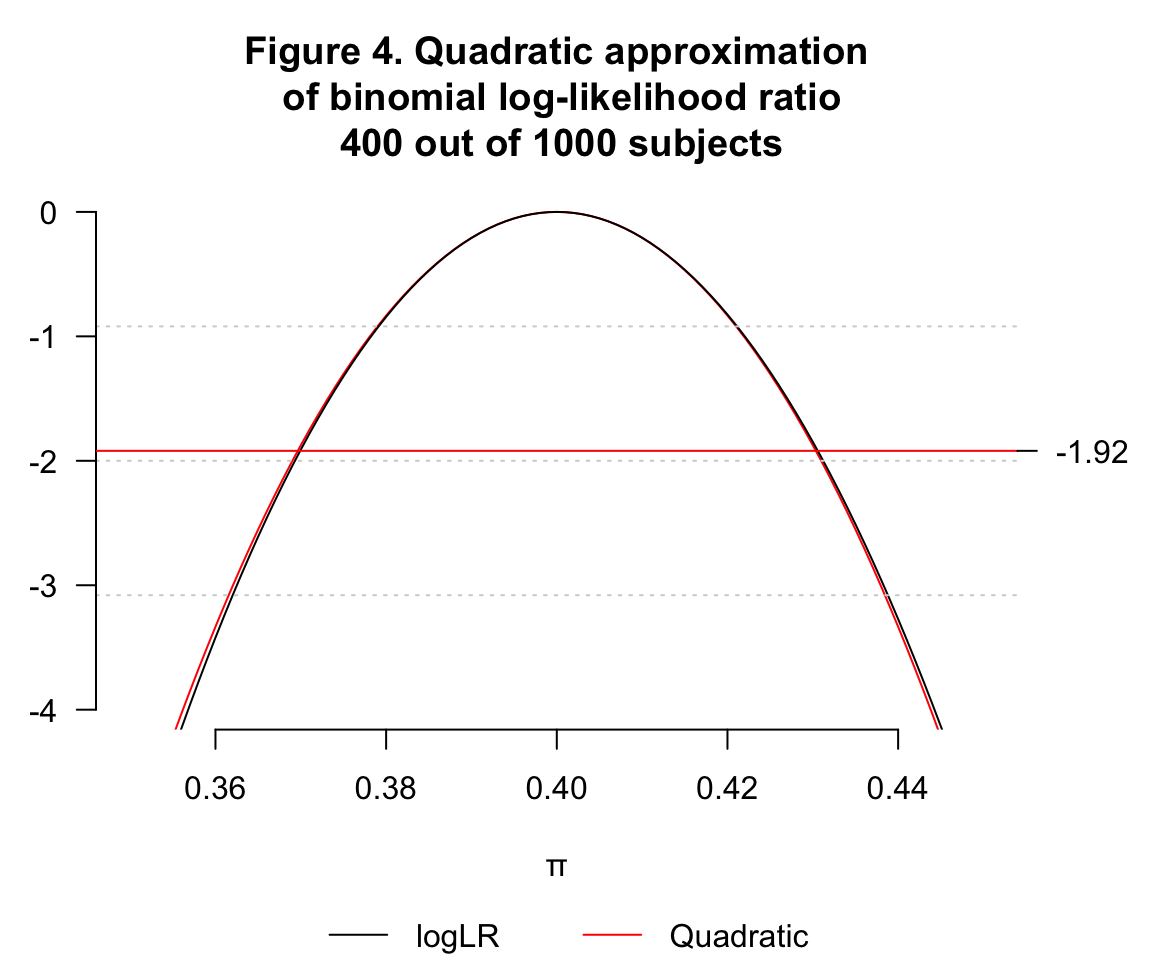
- \(\hat\pi=0.4, n=1000, k=400\)
- \(\hat\pi=0.01, n=100, k=1\)
注意此圖中紅線提示的近似二次曲線,信賴區間的下限已經低於0,是無法接受的近似。
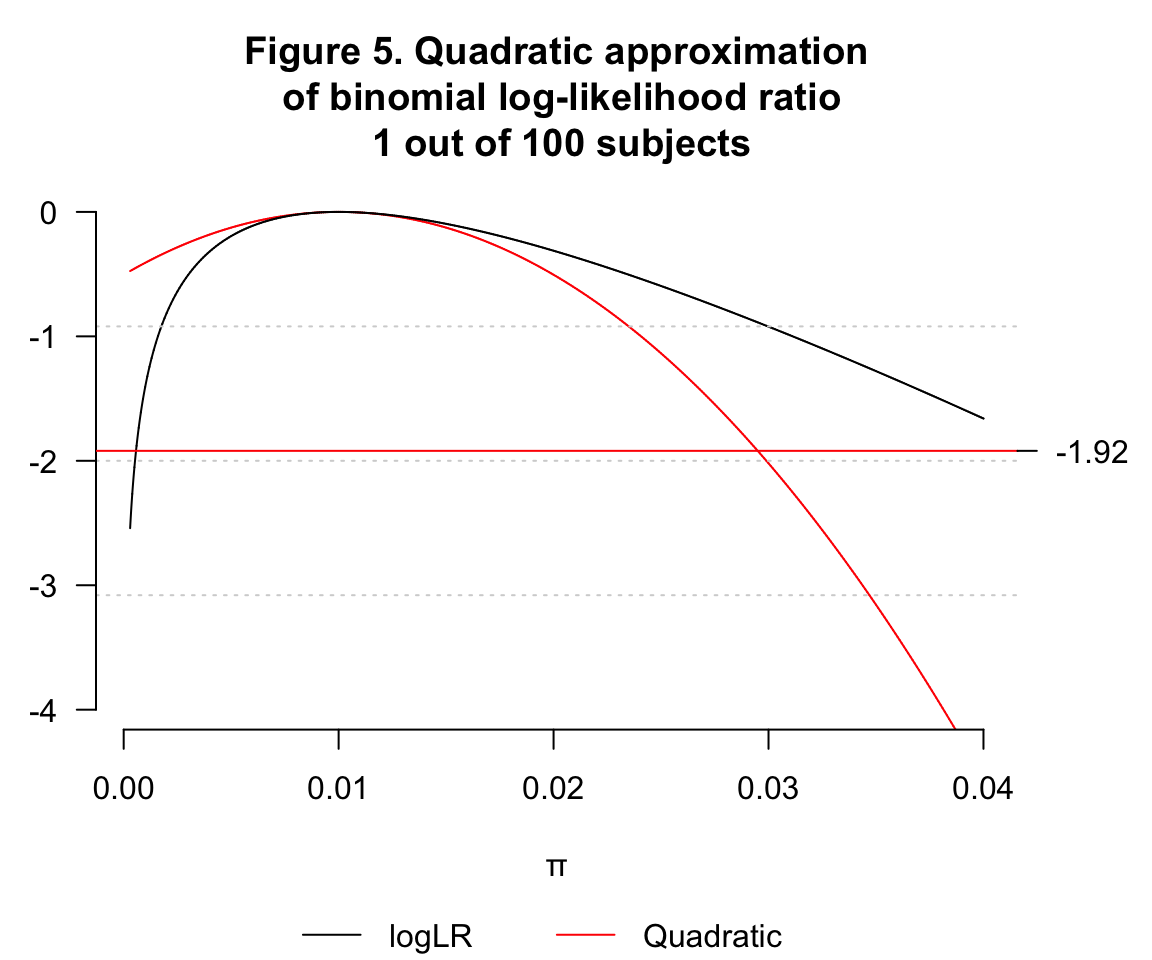
- \(\hat\pi=0.01, n=1000, k=10\)
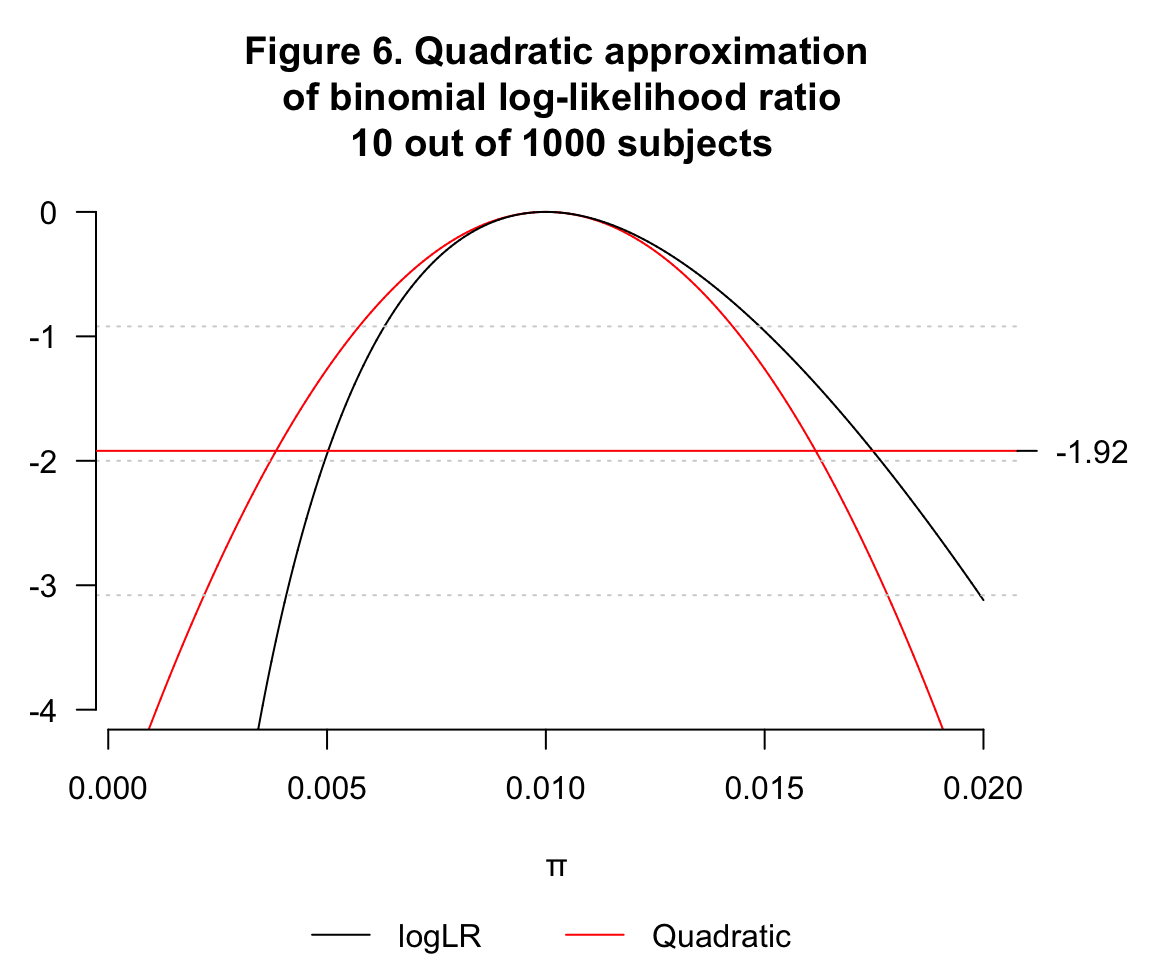
- \(\hat\pi=0.01, n=10000, k=100\)
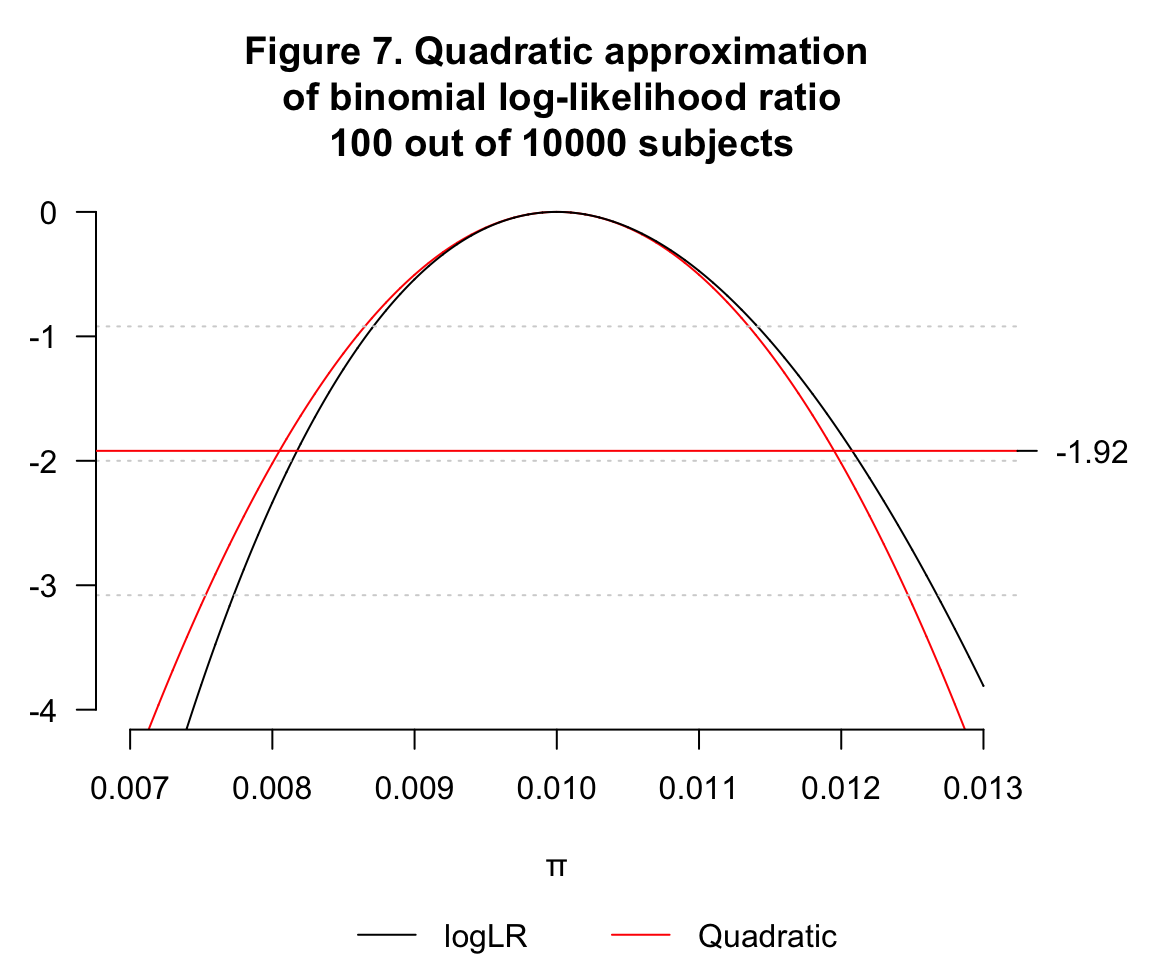
- \(\hat\pi=0.99, n=100, k=99\)
注意此圖中紅線提示的近似二次曲線,信賴區間的上限已經大於1,和上面的 Figure 5. 一樣也是無法接受的近似。
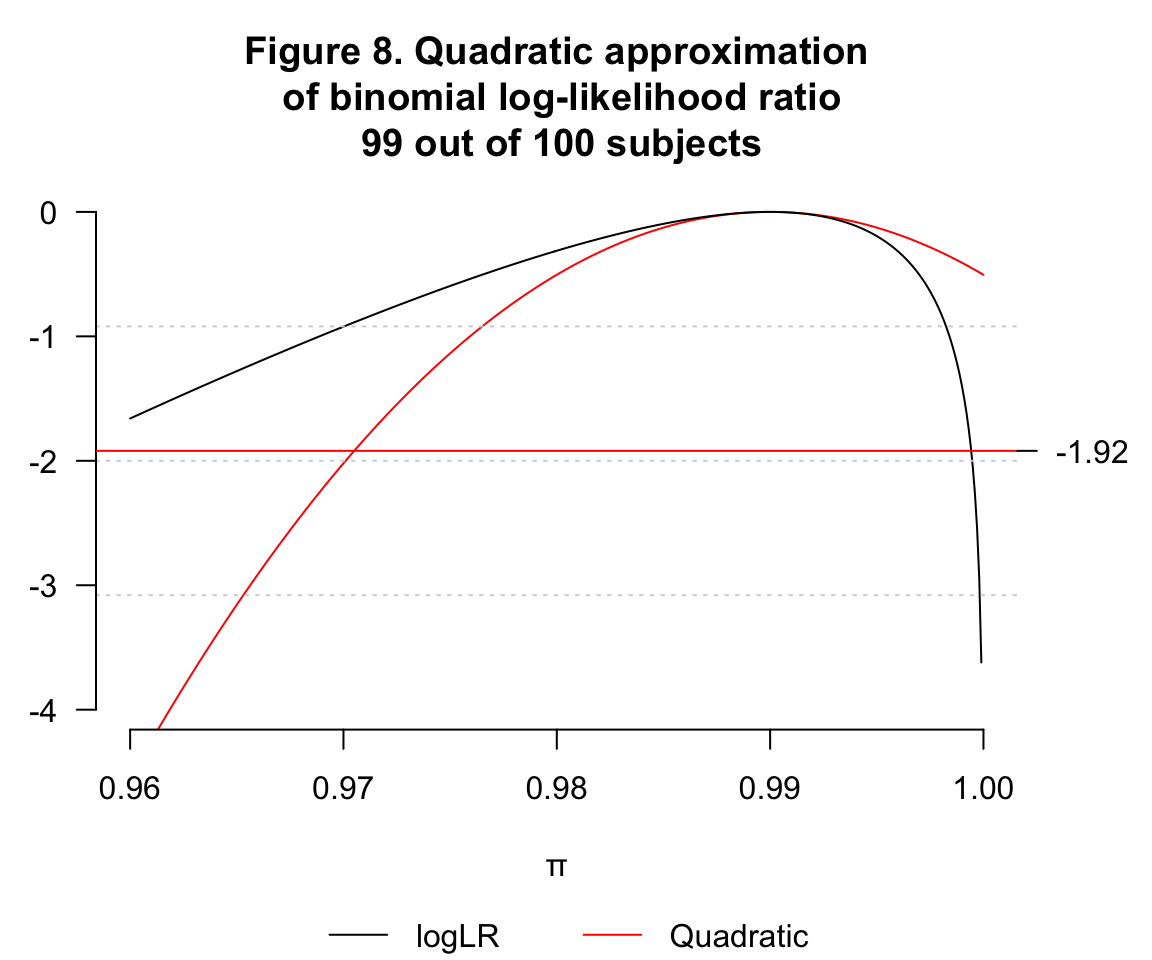
總結: 二次方程近似時,在二項分佈的情況下,隨着 \(n, k\) 增加,近似越理想。