似然非然 Likelihood
概率 vs. 推斷/Probability vs. Inference
在概率論的環境下,我們常常被告知的前提是:某某事件發生的概率是多少。例如: 一枚硬幣正面朝上的概率是 \(0.5\; Prob(coin\;landing\;heads)=0.5\)。然後在這個前提下,我們又繼續去計算複雜的事件發生的概率(例如,10次投擲硬幣以後4次正面朝上的概率是多少?)。
\[ \binom{10}{4}\times(0.5^4)\times(0.5^{10-4}) = 0.205 \]
dbinom(4, 10, 0.5)## [1] 0.2050781# or you can calculate by hand:
factorial(10)*(0.5^10)/(factorial(4)*(factorial(6)))## [1] 0.2050781在統計推斷的理論中,我們考慮實際的情況,這樣的實際情況就是,我們通過觀察獲得數據,然而我們並不知道某事件發生的概率到底是多少(神如果存在話,只有神知道)。故這個 \(Prob(coin\;landing\;heads)\) 的概率大小對於“人類”來說是未知的。我們可能觀察到投擲了10次硬幣,其中有4次是正面朝上的。那麼我們從這一次觀察實驗中,需要計算的是能夠符合觀察結果的“最佳”概率估計 (best estimate)。在這種情況下,似然法 (likelihood) 就是我們進行參數估計的最佳手段。
似然和極大似然估計
此處用二項分佈的例子來理解似然法的概念:假設我們觀察到10個對象中有4個患病,我們假定這個患病的概率爲 \(\pi\)。於是我們就有了下面的模型:
模型: 我們假定患病與否是一個服從二項分佈的隨機變量,\(X\sim Bin(10,\pi)\)。同時也默認每個人之間是否患病是相互獨立的。
數據: 觀察到的數據是,10人中有4人患病。於是 \(x=4\)。
現在按照觀察到的數據,參數 \(\pi\) 變成了未知數:
\[Prob(X=4|\pi)=\binom{10}{4}\pi^4(1-\pi)^{10-4}\]
此時我們會很自然的考慮,當 \(\pi\) 是未知數的時候,它取值爲多大的時候才能讓這個事件(即:10人中4人患病)發生的概率最大? 所以我們可以將不同的數值代入 \(\pi\) 來計算該事件在不同概率的情況下發生的可能性到底是多少:
| \(\pi\) | 事件 \(X=4\) 發生的概率 |
|---|---|
| 0.0 | 0.000 |
| 0.2 | 0.088 |
| 0.4 | 0.251 |
| 0.5 | 0.205 |
| 0.6 | 0.111 |
| 0.8 | 0.006 |
| 1.0 | 0.000 |
很顯然,如果 \(\pi=0.4\) 時,我們觀察到的事件發生的概率要比 \(\pi\) 取其它值時更大。於是小總結一下目前爲止的步驟如下:
- 觀察到實驗數據(10人中4個患病);
- 假定這數據服從二項分佈的概率模型,計算不同(\(\pi\) 的取值不同的)情況下,該事件按照假定模型發生的概率;
- 通過比較,我們選擇了能夠讓觀察事件發生概率最高的參數取值 (\(\pi=0.4\))。
至此,我們可以知道,似然方程,是一個關於未知參數 \(\pi\) 的函數,我們目前位置做的就是找到這個函數的最大值 (maximised),和使之成爲最大值時的 \(\pi\) :
\[L(\pi|X=4)=\binom{10}{4}\pi^4(1-\pi)^{10-4}\]
我們可以畫出這個似然方程的形狀, \(\pi\in[0,1]\)
x <- seq(0,1,by=0.001)
y <- (factorial(10)/(factorial(4)*(factorial(6))))*(x^4)*((1-x)^6)
plot(x, y, type = "l", ylim = c(0,0.3), ylab = "L(\U03C0)", xlab = "\U03C0")
title("Figure 1. Binomial Likelihood")
abline(h=0.251, lty=2)
abline(v=0.4, lty=2)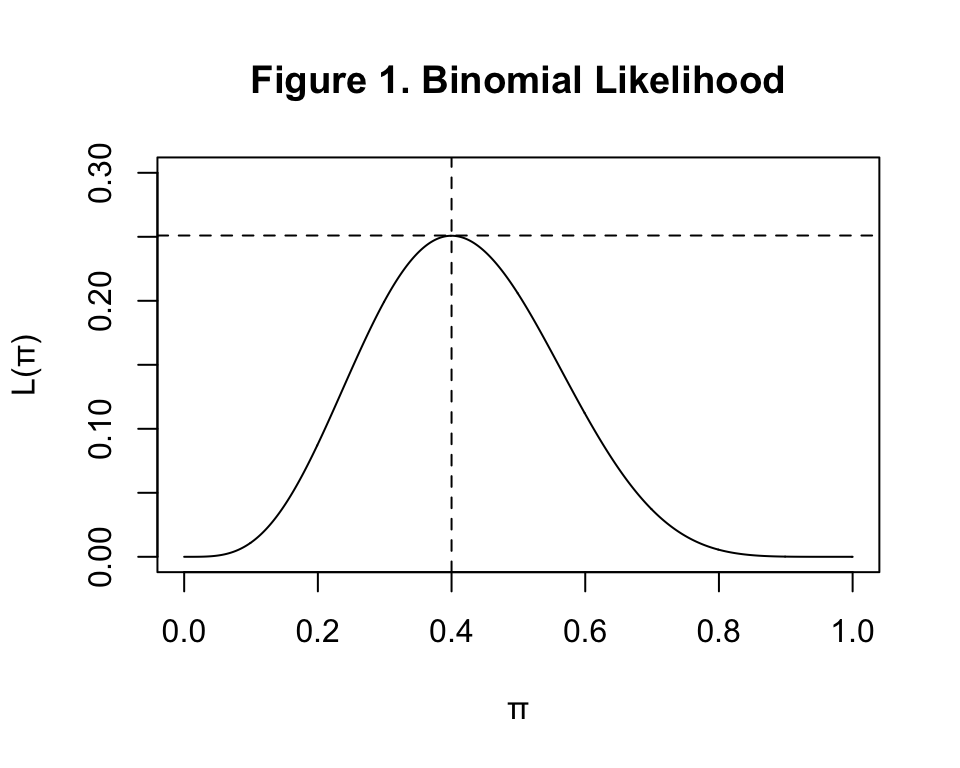
從圖形上我們也能確認,\(\pi=0.4\) 時能夠讓這個似然方程取得最大值。
似然方程的一般化定義
對於一個概率模型,如果其參數爲 \(\theta\),那麼在給定觀察數據 \(\underline{x}\) 時,該參數的似然方程被定義爲:
\(L(\theta|\underline{x})=P(\underline{x}|\theta)\)
注意:
- \(P(\underline{x}|\theta)\) 可以是概率(離散分佈)方程,也可以是概率密度(連續型變量)方程。對於此方程,\(\theta\) 是給定的,然後再計算某些事件發生的概率。
- \(L(\theta|\underline{x})\) 是一個關於參數 \(\theta\) 的方程,此時,\(\underline{x}\) 是固定不變的(觀察值)。我們希望通過這個方程求出能夠使觀察到的事件發生概率最大的參數值。
- 似然方程不是一個概率密度方程。
另一個例子:
有一組觀察數據是離散型隨機變量 \(X\),它符合概率方程 \(f(x|\theta)\)。下表羅列了當 \(\theta\) 分別取值 \(1,2,3\) 時的概率方程的值,試求每個觀察值 \(X = 0,1,2,3,4\) 的最大似然參數估計:
| \(x\) | \(f(x|1)\) | \(f(x|2)\) | \(f(x|3)\) |
|---|---|---|---|
| 0 | 1/3 | 1/4 | 0 |
| 1 | 1/3 | 1/4 | 0 |
| 2 | 0 | 1/4 | 1/6 |
| 3 | 1/6 | 1/4 | 1/2 |
| 4 | 1/6 | 0 | 1/3 |
| \(x\) | \(f(x|1)\) | \(f(x|2)\) | \(f(x|3)\) | \(\theta\) |
|---|---|---|---|---|
| 0 | 1/3 | 1/4 | 0 | 1 |
| 1 | 1/3 | 1/4 | 0 | 1 |
| 2 | 0 | 1/4 | 1/6 | 2 |
| 3 | 1/6 | 1/4 | 1/2 | 3 |
| 4 | 1/6 | 0 | 1/3 | 3 |
對數似然方程 log-likelihood
似然方程的最大值,可通過求 \(L(\theta|data)\) 的最大值獲得,也可以通過求該方程的對數方程 \(\ell(\theta|data)\) 的最大值獲得。傳統上,我們估計最大方程的最大值的時候,會給參數戴一頂“帽子”(因爲這是觀察獲得的數據告訴我們的參數): \(\hat{\theta}\)。並且我們發現對數似然方程比一般的似然方程更加容易微分,因此求似然方程的最大值就變成了求對數似然方程的最大值:
\[\frac{d\ell}{d\theta}=\ell^\prime(\theta)=0\\ AND\\ \frac{d^2\ell}{d\theta^2}<0\]
要注意的是,微分不一定總是能幫助我們求得似然方程的最大值。如果說參數本身的定義域是有界限的話,微分就行不通了:
x <- seq(0,3,by=0.001)
y <- (x-1)^2-5
plot(x, y, type = "l", ylim = c(-5,0-1), ylab = "L(\U03B8)", xlab = "\U03B8")
title("Figure 2. Likelihood function with \n a limited domain")
abline(v=3, lty=2)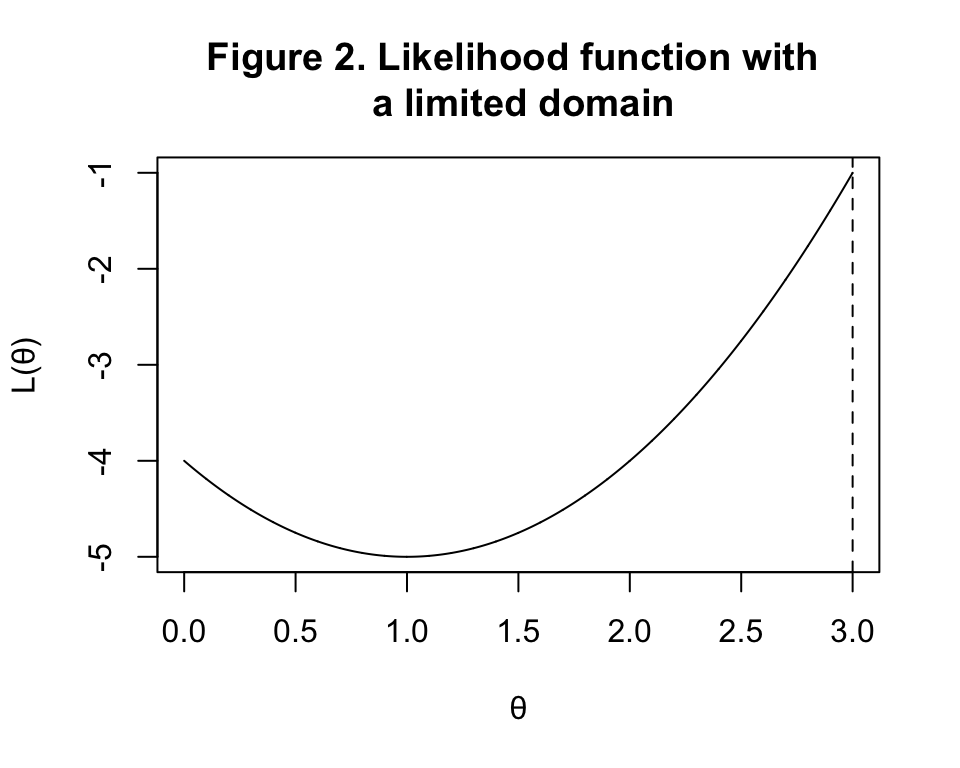
證明:當 \(L(\theta|data)\) 取最大值時,該方程的對數方程 \(\ell(\theta|data)\) 也是最大值:
如果似然方程是連續可導,只有一個最大值,且可以二次求導,假設 \(\hat{\theta}\) 使該方程取最大值,那麼:
\[\frac{dL}{d\theta}=0, \frac{d^2L}{d\theta^2}<0 \Rightarrow \theta=\hat{\theta}\]
令 \(\ell=logL\) 那麼 \(\frac{d\ell}{dL}=\ell^\prime=\frac{1}{L}\):
\[\frac{d\ell}{d\theta}=\frac{d\ell}{dL}\cdot\frac{dL}{d\theta}=\frac{1}{L}\cdot\frac{dL}{d\theta}\]
當 \(\ell(\theta|data)\) 取最大值時:
\[\frac{d\ell}{d\theta}=0\Leftrightarrow\frac{1}{L}\cdot\frac{dL}{d\theta}=0\\ \because \frac{1}{L}\neq0 \\ \therefore \frac{dL}{d\theta}=0\\ \Leftrightarrow \theta=\hat{\theta}\]
\[ \begin{aligned} \frac{d^2\ell}{d\theta^2} &= \frac{d}{d\theta}(\frac{d\ell}{dL}\cdot\frac{dL}{d\theta})\\ &= \frac{d\ell}{dL}\cdot\frac{d^2L}{d\theta^2} + \frac{dL}{d\theta}\cdot\frac{d}{d\theta}(\frac{d\ell}{dL}) \end{aligned} \]
當 \(\theta=\hat{\theta}\) 時,\(\frac{dL}{d\theta}=0\) 且 \(\frac{d^2L}{d\theta^2}<0 \Rightarrow \frac{d^2\ell}{d\theta^2}<0\)
所以,求獲得 \(\ell(\theta|data)\) 最大值的 \(\theta\) 即可令 \(L(\theta|data)\) 獲得最大值。
極大似然估計 (maximum likelihood estimator, MLE) 的性質:
- 漸進無偏 Asymptotically unbiased:
\(n\rightarrow \infty \Rightarrow E(\hat{\Theta}) \rightarrow \theta\) - 漸進最高效能 Asymptotically efficient:
\(n\rightarrow \infty \Rightarrow Var(\hat{\Theta})\) 是所有參數中方差最小的估計 - 漸進正態分佈 Asymptotically normal:
\(n\rightarrow \infty \Rightarrow \hat{\Theta} \sim N(\theta, Var(\hat{\Theta}))\) - 變形後依然保持不變 Transformation invariant:
\(\hat{\Theta}\) 是 \(\theta\) 的MLE時 \(\Rightarrow g(\hat{\Theta})\) 是 \(g(\theta)\) 的 MLE - 信息足夠充分 Sufficient:
\(\hat{\Theta}\) 包含了觀察數據中所有的能夠用於估計參數的信息 - 始終不變 consistent:
\(n\rightarrow\infty\Rightarrow\hat{\Theta}\rightarrow\theta\) 或者可以寫成:\(\varepsilon>0, lim_{n\rightarrow\infty}P(|\hat{\Theta}-\theta|>\varepsilon)=0\)
率的似然估計 Likelihood for a rate
如果在一項研究中,參與者有各自不同的追蹤隨訪時間(長度),那麼我們應該把事件(疾病)的發病率用率的形式(多少事件每單位人年, e.g. per person year of observation)。如果這個發病率的參數用 \(\lambda\) 來表示,所有參與對象的隨訪時間之和爲 \(p\) 人年。那麼這段時間內的期望事件(疾病發病)次數爲:\(\mu=\lambda p\)。假設事件(疾病發病)發生是相互獨立的,可以使用泊松分佈來模擬期望事件(疾病發病)次數 \(D\):
\[D\sim Poi(\mu)\]
假設我們觀察到了 \(D=d\) 個事件,我們獲得這個觀察值的概率應該用以下的模型:
\[Prob(D=d)=e^{-\mu}\frac{\mu^d}{d!}=e^{-\lambda p}\frac{\lambda^dp^d}{d!}\]
因此,\(\lambda\) 的似然方程是:
\[L(\lambda|observed \;data)=e^{-\lambda p}\frac{\lambda^dp^d}{d!}\]
所以,\(\lambda\) 的對數似然方程是:
\[ \begin{aligned} \ell(\lambda|observed\;data) &= log(e^{-\lambda p}\frac{\lambda^dp^d}{d!}) \\ &= -\lambda p+d\:log(\lambda)+d\:log(p)-log(d!) \\ \end{aligned} \]
解 \(\ell^\prime(\lambda|data)=0\):
\[ \begin{aligned} \ell^\prime(\lambda|data) &= -p+\frac{d}{\lambda}=0\\ \Rightarrow \hat{\lambda} &= \frac{d}{p} \\ \end{aligned} \]
注意: 在對數似然方程中,不包含參數的部分,對與似然方程的形狀不產生任何影響,我們在微分對數似然方程的時候,這部分也都自動消失。所以不包含參數的部分,與我們如何獲得極大似然估計是無關的。因此,我們常常在寫對數似然方程的時候就把其中沒有參數的部分直接忽略了。例如上面泊松分佈的似然方程中,\(d\:log(p)-log(d!)\) 不包含參數 \(\lambda\) 可以直接不寫出來。
有 \(n\) 個獨立觀察時的似然方程和對數似然方程
當有多個獨立觀察時,總體的似然方程等於各個觀察值的似然方程之乘積。如果 \(X_1,\dots,X_n\stackrel{i.i.d}{\sim}f(\cdot|\theta)\)
\[L(\theta|x_1,\cdots,x_n)=f(x_1,\cdots,x_n|\theta)=\prod_{i=1}^nf(x_i|\theta)\\ \Rightarrow \ell(\theta|x_1,\cdots,x_n)=\sum_{i=1}^nlog(f(x_i|\theta))\]