「統計解析のための線形代数」復習筆記18
行列式的定義與計算
\(n\)次正方形矩陣 \(A\) 的行列式(\(n\)次行列式),被記作:
\(|A|, |a_{ij}|, \det(A), \det(a_{ij}), \begin{vmatrix} a_{11}& a_{12} & \cdots & a_{1n}\\ a_{21}& a_{22} & \cdots & a_{2n}\\ \vdots& \vdots & \ddots & \vdots\\ a_{n1}& a_{n2} & \cdots & a_{nn} \notag \end{vmatrix}\)
1次行列式: \[\begin{equation} A=(a_{11}), |A|=a_{11} (\#eq:determinant1) \end{equation}\]
2次行列式: \[\begin{equation} A=\left( \begin{array}{} a_{11} & a_{12}\\ a_{21} & a_{22}\\ \end{array} \right), |A|=a_{11}a_{12}-a_{12}a_{21} (\#eq:determinant2) \end{equation}\]
\(n-1\) 次行列式 \[\begin{equation} A_{(n-1)\times(n-1)}, 假設行列式 |A| 有被定義 (\#eq:determinant3) \end{equation}\]
\(n\) 次行列式
假如(??)成立:
對於:\(A_{n\times n}=\left( \begin{array}{c} a_{11}& a_{12} & \cdots & a_{1n}\\ a_{21}& a_{22} & \cdots & a_{2n}\\ \vdots& \vdots & \ddots & \vdots\\ a_{n1}& a_{n2} & \cdots & a_{nn} \end{array} \right)\\ |A|=\begin{vmatrix} a_{11}& a_{12} & \cdots & a_{1n}\\ a_{21}& a_{22} & \cdots & a_{2n}\\ \vdots& \vdots & \ddots & \vdots\\ a_{n1}& a_{n2} & \cdots & a_{nn} \notag \end{vmatrix}\\ \left\{ \begin{array}{} (4)\;=a_{i1}A_{i1}+a_{i2}A_{i2}+\cdots+a_{ij}A_{ij}+\cdots+a_{in}A_{in}\\ (5)\;=a_{1j}A_{i1}+a_{2j}A_{2j}+\cdots+a_{ij}A_{ij}+\cdots+a_{nj}A_{nj}\\ \end{array} \right.\)
式子 \((4)\) 被稱爲行列式 \(|A|\) 的第 \(i\) 行展開式(expansion of \(|A|\) according to elements of row \(i\))。同樣的,式子 \((5)\) 被稱爲行列式 \(|A|\) 的第 \(j\) 列展開式。\(|A_{ij}|(i=1,2,\cdots,n;j=1,2,\cdots,n)\) 被稱爲 成分 \(a_{ij}\) 的餘因子(cofactor),定義如下:
\(A_{ij}=(-1)^{i+j}D_{ij}\\ \;\;\;\;=(-1)^{i+j}\begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1,j-1} & a_{1,j+1} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2,j-1} & a_{2,j+1} & \cdots & a_{2n}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots\\ a_{i-1,1} & a_{i-1,2} & \cdots & a_{i-1,j-1} & a_{i-1,j+1} & \cdots & a_{i-1,n}\\ a_{i+1,1} & a_{i+1,2} & \cdots & a_{i+1,j-1} & a_{i+1,,j+1} & \cdots & a_{i+1,n}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots\\ a_{11} & a_{12} & \cdots & a_{1,j-1} & a_{1,j+1} & \cdots & a_{1n}\\ \end{vmatrix}\)
\(D_{ij}\) 正如上面等式最右端所寫,其實是行列式 \(A_{n\times n}\) 剔除了第 \(i\) 行和第 \(j\) 列的 \((n-1)\) 次行列式,又被叫做行列式 \(A_{n\times n}\) 的小行列式(minor)。
餘因子矩陣
以 \(A_{n\times n}\) 的成分 \(a_{ij}\) 的餘因子 \(A_{ij}\) 作成分的矩陣的轉置矩陣作被稱爲 \(A_{n\times n}\) 的餘因子矩陣(adjoint matrix, adjugate matrix)。標記爲 \(adj(A)\)。也就是說:
\(adj(A)=\left( \begin{array}{c} A_{11}& A_{12} & \cdots & A_{1n}\\ A_{21}& A_{22} & \cdots & A_{2n}\\ \vdots& \vdots & \ddots & \vdots\\ A_{n1}& A_{n2} & \cdots & A_{nn} \end{array} \right)^t=\left( \begin{array}{c} A_{11}& A_{21} & \cdots & A_{n1}\\ A_{12}& A_{22} & \cdots & A_{n2}\\ \vdots& \vdots & \ddots & \vdots\\ A_{1n}& A_{2n} & \cdots & A_{nn} \end{array} \right)\)
我們來試着計算行列式:
1. \(2\) 次行列式
以方程(??)的定義計算:
\(\begin{vmatrix} a_{11} & a_{12}\\ a_{21} & a_{22}\\ \end{vmatrix}=a_{11}a_{22}-a_{12}a_{21}\)
此公式可以用下列 示意圖(薩呂法則, Sarrus’ rule) 來記憶:
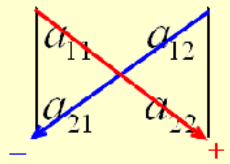
也就是,沿着右下方向將所有成分相乘以後用加號 \(+\) 號連接起來,沿着左下的方向的所有成分則相乘以後用減號 \(-\) 號連接起來。最後將這兩者相加獲得行列式的值。
練習: 求 \(A=\left( \begin{array}{} 4 & 2\\ 1 & 3\\ \end{array} \right)\) 的行列式和餘因子矩陣。
解: \(|A|=\begin{vmatrix} 4 & 2\\ 1 & 3\\ \end{vmatrix}=4\times3-2\times1=10\)
\(adj(A)=\left( \begin{array}{} A_{11} & A_{21}\\ A_{12} & A_{22}\\ \end{array} \right)\)
\(\because A_{11}=(-1)^{(1+1)}\times3\\ A_{21}=(-1)^{(2+1)}\times2\\ A_{12}=(-1)^{(1+2)}\times1\\ A_{22}=(-1)^{2+2}\times4\\ \therefore adj(A)=\left( \begin{array}{r} 3 & -2\\ -1 & 4\\ \end{array} \right)\)
注意:餘因子矩陣,終究是一個矩陣而非行列式。
- 三次矩陣
\(A=\left( \begin{array}{c} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{array} \right)\) 的行列式 \(|A|\) 要如何用 \(A\) 的成分來表示呢?
我們發現,代入上面第 \((4)\) 個式子 \(n=3\) 的情況來計算。
在這裏,我們就按照 \(i=1\) 的情況來展開。 (注意:\(i=2, i=3\) 的情況展開,結果也是一樣的。)
\[\begin{align} |A| &= a_{11}A_{11}+a_{12}A_{12}+a_{13}A_{13}\\ &= a_{11}(-1)^{1+1}D_{11}+a_{12}(-1)^{1+2}D_{12}\\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;+a_{13}(-1)^{1+3}D_{13}\\ &= a_{11}\begin{vmatrix}a_{22} & a_{23}\\ a_{32} & a_{33}\\\end{vmatrix}-a_{12}\begin{vmatrix}a_{21} & a_{23}\\ a_{31} & a_{33}\\\end{vmatrix}\\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;+a_{13}\begin{vmatrix}a_{21} & a_{22}\\ a_{31} & a_{32}\\\end{vmatrix}\\ &= a_{11}(a_{22}a_{23}-a_{23}a_{32})-a_{12}(a_{21}a_{33}-a_{31}a_{23})\\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;+a_{13}(a_{21}a_{32}-a_{22}a_{31})\\ &=a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{11}a_{23}a_{32}\\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;-a_{12}a_{21}a_{33}-a_{13}a_{22}a_{31} \end{align}\]
我們也可以利用薩呂法則(下圖)來記住計算過程:
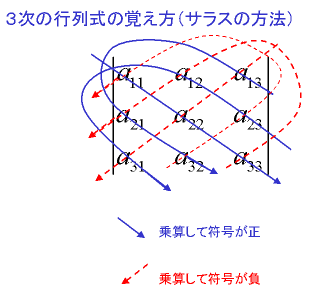
另外,可以得到如下的餘因子:
\(A_{11}=\begin{vmatrix}a_{22} & a_{23}\\ a_{32} & a_{33}\\\end{vmatrix}, A_{12}=-\begin{vmatrix}a_{21} & a_{23}\\ a_{31} & a_{33}\\\end{vmatrix}, A_{13}=\begin{vmatrix}a_{21} & a_{22}\\ a_{31} & a_{32}\\\end{vmatrix}\\ A_{21}=-\begin{vmatrix}a_{12} & a_{13}\\ a_{32} & a_{33}\\\end{vmatrix}, A_{22}=\begin{vmatrix}a_{11} & a_{13}\\ a_{31} & a_{33}\\\end{vmatrix}, A_{23}=-\begin{vmatrix}a_{11} & a_{12}\\ a_{31} & a_{32}\\\end{vmatrix}\\ A_{31}=\begin{vmatrix}a_{12} & a_{13}\\ a_{22} & a_{23}\\\end{vmatrix}, A_{32}=-\begin{vmatrix}a_{11} & a_{13}\\ a_{21} & a_{23}\\\end{vmatrix}, A_{33}=\begin{vmatrix}a_{11} & a_{12}\\ a_{21} & a_{22}\\\end{vmatrix}\)
因此餘因子矩陣爲:
\(adj(A)=\left( \begin{array}{c} A_{11} & A_{12} & A_{13}\\ A_{21} & A_{22} & A_{23}\\ A_{31} & A_{32} & A_{33}\\ \end{array} \right)^t=\left( \begin{array}{c} A_{11} & A_{21} & A_{23}\\ A_{12} & A_{22} & A_{32}\\ A_{13} & A_{23} & A_{33}\\ \end{array} \right)\)
| 練習:試求矩陣 \(A=\left( \begin{array}{r} 6 & 1 & -3\\ 3 & 5 & 7\\ 2 & -1 & 3\\ \end{array} \right)\) 的行列式和餘因子矩陣 |
| 解: \(|A|= \begin{vmatrix} 6 & 1 & -3\\ 3 & 5 & 7\\ 2 & -1 & 3\\ \end{vmatrix}\\ \;\;\;\;\:=6\times5\times3+1\times7\times2+(-3)\times3\times(-1)\\ \;\;\;\;\;\:\;\;\;\;\:-\{6\times7\times(-1)+1\times3\times3+(-3)\times5\times2\}\\ \;\;\;\;\:=113-(-63)=176\\ \\ A_{11}=\begin{vmatrix}5 & 7\\ -1 & 3\\\end{vmatrix}=15-(-7)=22\\ A_{12}=\begin{vmatrix}3 & 7\\ 2& 3\\\end{vmatrix}=9-14=-5\\ A_{13}=\begin{vmatrix}3 & 5\\ 2 & -1\\\end{vmatrix}=-3-10=-13\\ A_{21}=\begin{vmatrix}1 & -3\\ -1 & 3\\\end{vmatrix}=3-3=0\\ A_{22}=\begin{vmatrix}6 & -3\\ 2 & 3\\\end{vmatrix}=18-(-6)=24\\ A_{23}=\begin{vmatrix}6 & 1\\ 2 & -1\\\end{vmatrix}=-6-2=-8\\ A_{31}=\begin{vmatrix}1 & -3\\5 & 7\\\end{vmatrix}=7-(-15)=22\\ A_{32}=\begin{vmatrix}6 & -3\\3 & 7\\\end{vmatrix}=42-(-9)=51\\ A_{33}=\begin{vmatrix}6 & 1\\ 3 & 5\\\end{vmatrix}=30-3=27\\ \Longrightarrow adj(A)=\left( \begin{array}{r} 22 & 5 & -13 \\ 0 & 24& -8 \\ 22 & 51& 27 \\ \end{array} \right)^t=\left( \begin{array}{r} 22 & 0 & 22\\ 5 & 24 & 51\\ -13 & -8 & 27\\ \end{array} \right)\) |
| 練習: 求3次矩陣的固有值時(將來敘述)需要的行列式 \(\begin{vmatrix} a-\lambda & b & c\\ d & e-\lambda & f\\ g & h & i-\lambda \end{vmatrix}\) 展開以後,整理爲關於 \(\lambda\) 的式子: |
| 解: \(\begin{vmatrix} a-\lambda & b & c\\ d & e-\lambda & f\\ g & h & i-\lambda \end{vmatrix}\\ =(a-\lambda)(e-\lambda)(i-\lambda)+bfg+dhc\\ \;\;\;\;\;-\{g(e-\lambda)c+bd(i-\lambda)+(a-\lambda)fh\}\\ =-\lambda^3+(a+e+i)\lambda^2+(bd+cg+fh-ae-ei-ai)\lambda\\ \;\;\;\;\;+(aei+bfg+cdh-afh-bdi-ecg)\) |
- 4次行列式:
試求\(A=\left( \begin{array}{} a_{11}& a_{12}& a_{13}& a_{14}\\ a_{21}& a_{22}& a_{23}& a_{24}\\ a_{31}& a_{32}& a_{33}& a_{34}\\ a_{41}& a_{42}& a_{43}& a_{44} \end{array} \right)\\ \;\;=\left( \begin{array}{r} -2 & 3 &4 & 1\\ 4 & 2& 0& 5\\ 2 &-3& -4& 2\\ 2 & 1& 2& -3 \end{array} \right)\)
的行列式 \(|A|\):
由於第2行有成分 \(a_{23}=0\) 我們以第二行展開行列式,因爲 \(a_{23}=0\),所以 \(a_{23}A_{23}=0\) 可以省略:
\(|A|=a_{21}A_{21}+a_{22}A_{22}+a_{24}A_{24}\\ \;\;\;\;\:=a_{21}(-1)^{2+1}D_{21}+a_{22}(-1)^{2+2}D_{22}+a_{24}(-1)^{2+4}D_{24}\)
\(\because A_{21}=(-1)^{2+1}\begin{vmatrix} a_{12} & a_{13} & a_{14}\\ a_{32} & a_{33} & a_{34}\\ a_{42} & a_{43} & a_{44}\\ \end{vmatrix}\\ \;\;\;\;\;\;\;\;\;=-\begin{vmatrix} 3 & 4 & 1\\ -3 & -4 & 2\\ 1 & 2& -3\\ \end{vmatrix}=6\\ A_{22}=(-1)^{2+2}\begin{vmatrix} a_{11} & a_{13} & a_{14}\\ a_{31} & a_{33} & a_{34}\\ a_{41} & a_{43} & a_{44}\\ \end{vmatrix}\\ \;\;\;\;\;\;\;\;\;=\begin{vmatrix} -2 & 4 &1\\ 2 & -4 &2\\ 2 & 2 &-3\\ \end{vmatrix}=36\\ A_{24}=(-1)^{2+4}\begin{vmatrix} a_{11} & a_{12} & a_{13}\\ a_{31} & a_{32} & a_{33}\\ a_{41} & a_{42} & a_{43}\\ \end{vmatrix}\\ \;\;\;\;\;\;\;\;\;=-\begin{vmatrix} -2 & 3 &4\\ 2 & -3 &-4\\ 2 & 1 &2\\ \end{vmatrix}=0\\ \therefore |A|=4\times6+2\times36+5\times0=96\)
然而,4次以上的矩陣的行列式計算,沒有類似薩呂法則的計算方法。