正態分佈

概率密度曲線 probability density function， PDF

• 一個隨機連續型變量 \(X\) 它的性質由一個對應的概率密度方程 (probability density function, PDF) 決定。

• 在給定的範圍區間內，如 \(a\sim b, (a < b)\)，它的概率滿足:

\[P(a\leqslant X \leqslant b) = \int_a^bf(x)dx\]

• 這個相關的方程，在 \(a\sim b\) 區間內的積分，就是這個連續變量在這個區間內取值的概率。

# R codes for drawing a standard normal distribution by using ggplot2
library(ggplot2)
p <- ggplot(data.frame(x=c(-3,3)), aes(x=x)) +
  stat_function(fun = dnorm)
p + annotate("text", x=2, y=0.3, parse=TRUE, label="frac(1, sqrt(2*pi)) * e ^(-z^2/2)") +
  theme(plot.subtitle = element_text(vjust = 1),
        plot.caption = element_text(vjust = 1),
        axis.text.x = element_text(size = 12),
        axis.text.y = element_text(size = 12),
        plot.title = element_text(size = 10, face = "bold", hjust = 0.5),
        panel.background = element_rect(fill = "ivory")) +
  labs(title = "Probability density functions \n for standard normal distribution",
       x = NULL, y = NULL) +
  stat_function(fun = dnorm,
                xlim = c(-1.3,0.4),
                geom = "area",fill="#00688B", alpha= 0.2)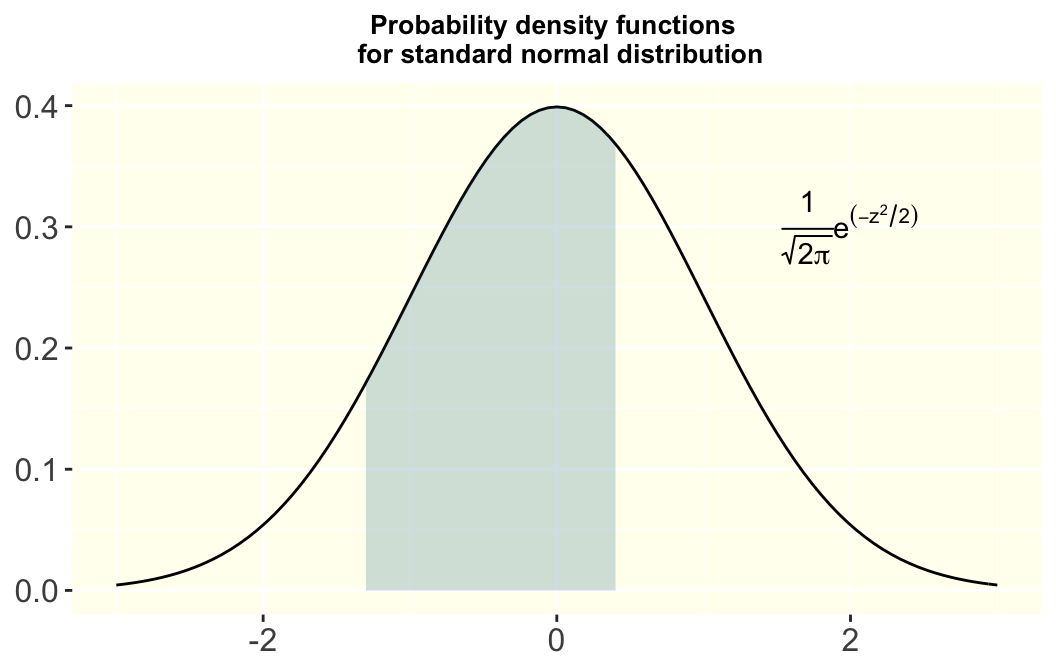

注意：整個方程的曲線下面積等於 \(1\)： \[\int_{-\infty}^\infty f(x)dx=1\]

• 期望 \(E(X)=\int_{-\infty}^\infty xf(x)dx\)
• 方差 \(Var(X)=\int_{-\infty}^\infty (x-\mu)^2f(x)dx\)

正態分佈

如果一組數據服從正態分佈，我們通常用它的期望（或者叫平均值）\(\mu\)，和它的方差 \(\sigma^2\)，來描述這組數據。記爲：

\[X \sim N(\mu, \sigma^2)\]

• 它的概率密度方程可以表述爲：

\[f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}exp(-\frac{(x-\mu)^2}{2\sigma^2})\]

• \(E(x) =\mu\)
• \(Var(x)=\sigma^2\)

標準正態分佈

標準正態分佈的期望（或者均值）爲 \(0\)，方差爲 \(1\)

• 記爲：\(Z \sim N(0,1)\)
• 它的概率密度方程表述爲：

\[\frac{1}{\sqrt{2\pi}}exp(-\frac{z^2}{2})\]

• 它的累積分佈方程 (cumulative distribution function， CDF)，是將概率密度方程 (PDF) 積分以後獲得的方程。通常我們記爲 \(\Phi(z)\)

再看一下標準正態分佈的概率密度方程曲線：

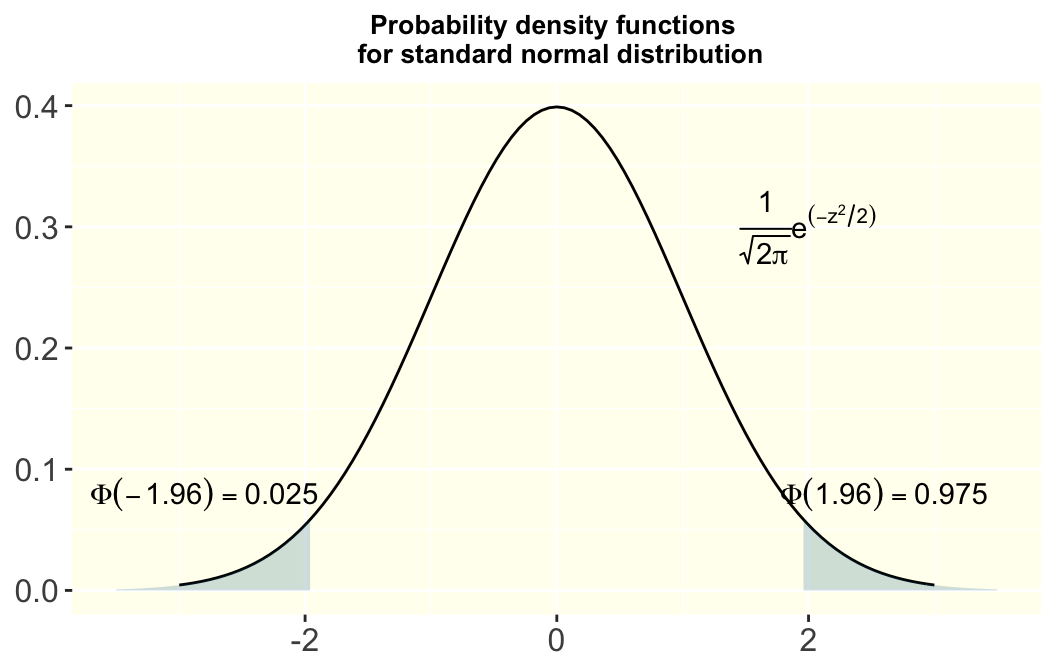
• 95% 的曲線下面積在標準差 standard deviation \(-1.96\sim1.96\) 之間的區域。
• 而且，\(\phi(-x)=1-\phi(x)\)
• 任何一個正態分佈都可以通過下面的公式，標準化成爲標準正態分佈：

\[Z=\frac{X-\mu}{\sigma}\]