你會用概率論來賭博嗎?
轉眼我已經進入課程的第二週了,總體來說,我們一半的時間都在電腦房練習 Stata 的數據清理和簡單的描述統計 (descriptive statistics)。從我個人的經驗來說,數據分析的過程,其實一大半的時間是消耗在 data cleaning 上的,即使手頭拿到了所謂的乾淨的數據,到真正要分析的時候就會發現一大堆的問題在裏面,需要重新整理,重新添加標記以使之變得更加讓人類可以讀懂。電腦是機器,他是不管你的數據是否乾淨的。只要你放了數據進去,邏輯還可以,沒有編程上的語法錯誤,它總歸會出來一些報告和結果的。如果就這麼直接用的話,大部分的人就會掉進陷阱。畢竟數據不光會說出事實真相,更多的情況下還會把真相給掩蓋住了。
我的其餘大部分時間都用在了複習高等數學的微積分上了。感覺好似回到了高中時代。其實大學的時候線性代數得分還是接近滿分的。後來多年不用,生疏了。剛打開複習的書的時候,許多微分積分的規則都已經忘記。通過這一週的辛苦練習,終於是找回了一點狀態。如果你也想有空的時候複習以下高中數學知識,這本書可以推薦給你:
Quick Calculus: Short Manual of Self-instruction

上面這本書的內容可以一邊閱讀,一邊練習。實在是複習的一本好書。我花了一週的課餘時間,從頭到尾把裏面的習題和解答全部完成。收穫很大。感覺年輕時的數學思維又開始在大腦裏復甦了。一身輕鬆。
下面想介紹一下上週學習的概率的基礎問題。
首先是最基礎的三個概率的公理:
- 對於任意事件 \(A\),它發生的概率 \(P(A)\) 滿足這樣的不等式: \(0 \leqslant P(A) \leqslant 1\)
- \(P(\Omega)=1\) , \(\Omega\) 是全樣本空間 (total sample space)
- 對於互斥(相互獨立)的事件 \(A_1, A_2, \dots, A_n\) 有如下的等式關係: \(P(A_1\cup A_2 \cup \cdots \cup A_n)=P(A_1)+P(A_2)+\cdots+P(A_n)\)
你是不是覺得上面三條公理都是廢話。
不用擔心,我也是這麼覺得的。因爲所有人都認同的道理,才能成爲公理 (axiom),因爲它們是不需要證明的自然而然形成的人人都接受的觀念。(axiom: a saying that is widely accepted on its own merits; its truth is assumed to be self-evident)
然而,正是這樣顯而易見的道理,確是拿來建築理論的基石,千萬不能小看了他們。例如,我們看下面這個看似也應該成爲公理的公式,你能證明嗎:
\(P(A_1\cup A_2) = P(A_1) + P(A_2) - P(A_1 \cap A_2)\)
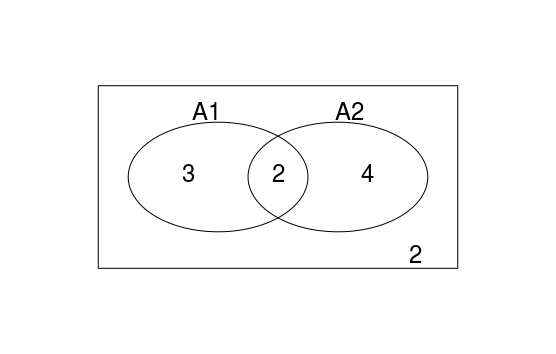
證明:
先考慮 \(A_1 \cup A_2\) 是什麼(拆分成三個互斥事件)
\(A_1 \cup A_2 = (A_1\cap \bar{A_2})\cup(\bar{A_1}\cap A_2)\cup(A_1\cap A_2)\)
運用上面的公理2 3
\(\therefore P(A_1 \cup A_2) = P(A_1\cap \bar{A_2}) + P(\bar{A_1}\cap A_2) + P(A_1\cap A_2) \;\;\;\;\;\;(1)\)
再考慮 \(A_1=(A_1\cap A_2)\cup(A_1\cap\bar{A_2})\) 繼續拆分成兩個互斥事件
\(\therefore P(A_1)=P(A_1\cap A_2)+P(A_1\cap\bar{A_2})\) 整理一下:
\(P(A_1\cap\bar{A_2})=P(A_1)-P(A_1\cap A_2)\)
同理可得: \(P(\bar{A_1}\cap A_2)=P(A_2)-P(A_1\cap A_2)\)
代入上面第(1)式可得:
\(P(A_1 \cup A_2) =P(A_1)-P(A_1\cap A_2)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;+P(A_2)-P(A_1\cap A_2)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;+P(A_1\cap A_2)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=P(A_1) + P(A_2) - P(A_1 \cap A_2)\)
條件概率 Conditional probability
- \(P(A|S)=\frac{P(A\cap S)}{P(S)}\)
- \(P(A\cap S) = P(A|S)P(S)\)
獨立 (independence) 的定義
- 兩個事件定義爲互爲獨立時 (\(A\) and \(B\) are said to be independent if and only if) \[P(A\cap B)=P(A)P(B)\]
- 因爲從條件概率的概念我們已知
\(P(A\cap B) = P(A|B)P(B)\)
所以\(P(A|B)=P(A)\) 即:事件 \(B\) 無法提供事件 \(A\) 的任何有效訊息 (\(A, B\) 互相獨立)
賭博問題
終於來到本次話題的重點了。我要扣題了哦。語文老師快在此加分。
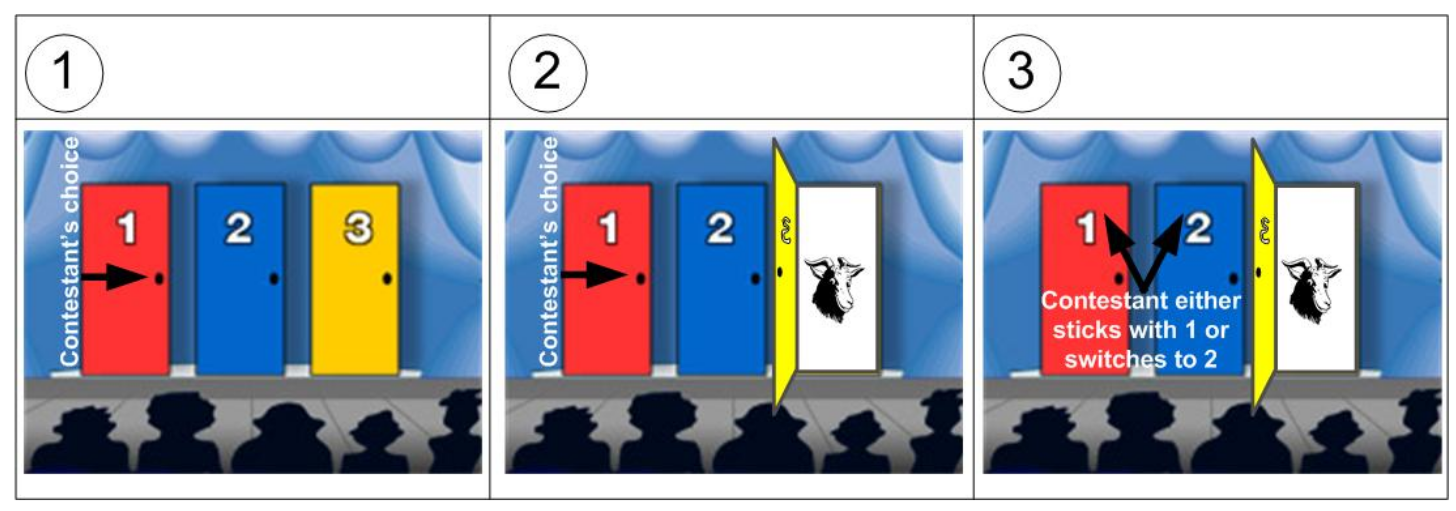
假設你在一個電視遊戲節目。有上圖一樣的三扇門。其中一扇門後面有一輛保時捷,另兩扇門後面則是(味道奇特的)山羊。遊戲規則是主持人會讓你先選擇其中一扇門(先不打開你選的這扇門)。主持人隨後打開另外兩扇門中的一扇沒有保時捷的門。主持人問你,你要堅持選擇之前選中的那扇門,還是要改變主意換一扇門去猜是否可以猜中保時捷。 請問,堅持選擇之前選中的門猜中保時捷的概率高,還是主持人打開一扇門以後改變主意猜中保時捷的概率更高呢?
答案明天揭曉。