 Thomas Bayes
Thomas Bayes等級線性回歸模型的 Rstan 貝葉斯實現
多層(等級)線性回歸模型/混合效應模型 multilevel/mixed effect regression model
關於等級線性回歸的基本知識和概念,請參考讀書筆記58-60章節。簡單來說,等級線性回歸通過給數據內部可能存在或者已知存在的結構或者層級增加隨機截距或者隨機斜率的方式來輔助解釋組間差異和組內的差異。
適用於等級線性回歸模型的數據
本章節使用的數據是四家大公司40名社員的年齡和年收入數據:
d <- read.csv(file='../../static/files/data-salary-2.txt')
d## X Y KID
## 1 7 457 1
## 2 10 482 1
## 3 16 518 1
## 4 25 535 1
## 5 5 427 1
## 6 25 603 1
## 7 26 610 1
## 8 18 484 1
## 9 17 508 1
## 10 1 380 1
## 11 5 453 1
## 12 4 391 1
## 13 19 559 1
## 14 10 453 1
## 15 21 517 1
## 16 12 553 2
## 17 17 653 2
## 18 22 763 2
## 19 9 538 2
## 20 18 708 2
## 21 21 740 2
## 22 6 437 2
## 23 15 646 2
## 24 4 422 2
## 25 7 444 2
## 26 10 504 2
## 27 2 376 2
## 28 15 522 3
## 29 27 623 3
## 30 14 515 3
## 31 18 542 3
## 32 20 529 3
## 33 18 540 3
## 34 11 411 3
## 35 26 666 3
## 36 22 641 3
## 37 25 592 3
## 38 28 722 4
## 39 24 726 4
## 40 22 728 4X: 社員年齡減去23獲得的數據(23歲是大部分人大學畢業入職時的年齡)Y: 年收入(萬日元)KID: 公司編號
我們認爲,年收入 Y,是基本平均年收入和隨機誤差(服從均值爲零,方差是 \(\sigma^2\) 的正態分佈)之和。且基本平均年收入和年齡成正比(年功序列型企業)。但是呢,因爲不同的公司入職時的基本收入可能不同,且可能隨着年齡增加而增長薪水的速度可能也不一樣。那麼由於不同公司所造成的差異,可以被認爲是組間差異。
確認數據分佈
這次分析的目的是要瞭解「每個公司KID內隨着年齡的增加而增長的薪水幅度是多少」,那麼我們要在結果報告中體現的就是每家公司的基本年收入,新入職時的年收入,以及隨着年齡增長而上升的薪水的事後分佈。
我們先來看把四家公司職員放在一起時的整體圖形:
library(ggplot2)
d$KID <- as.factor(d$KID)
res_lm <- lm(Y ~ X, data=d)
coef <- as.numeric(res_lm$coefficients)
p <- ggplot(d, aes(X, Y, shape=KID))
p <- p + theme_bw(base_size=18)
p <- p + geom_abline(intercept=coef[1], slope=coef[2], size=2, alpha=0.3)
p <- p + geom_point(size=2)
p <- p + scale_shape_manual(values=c(16, 2, 4, 9))
p <- p + labs(x='X (age-23)', y='Y (10,000 Yen/year)')
p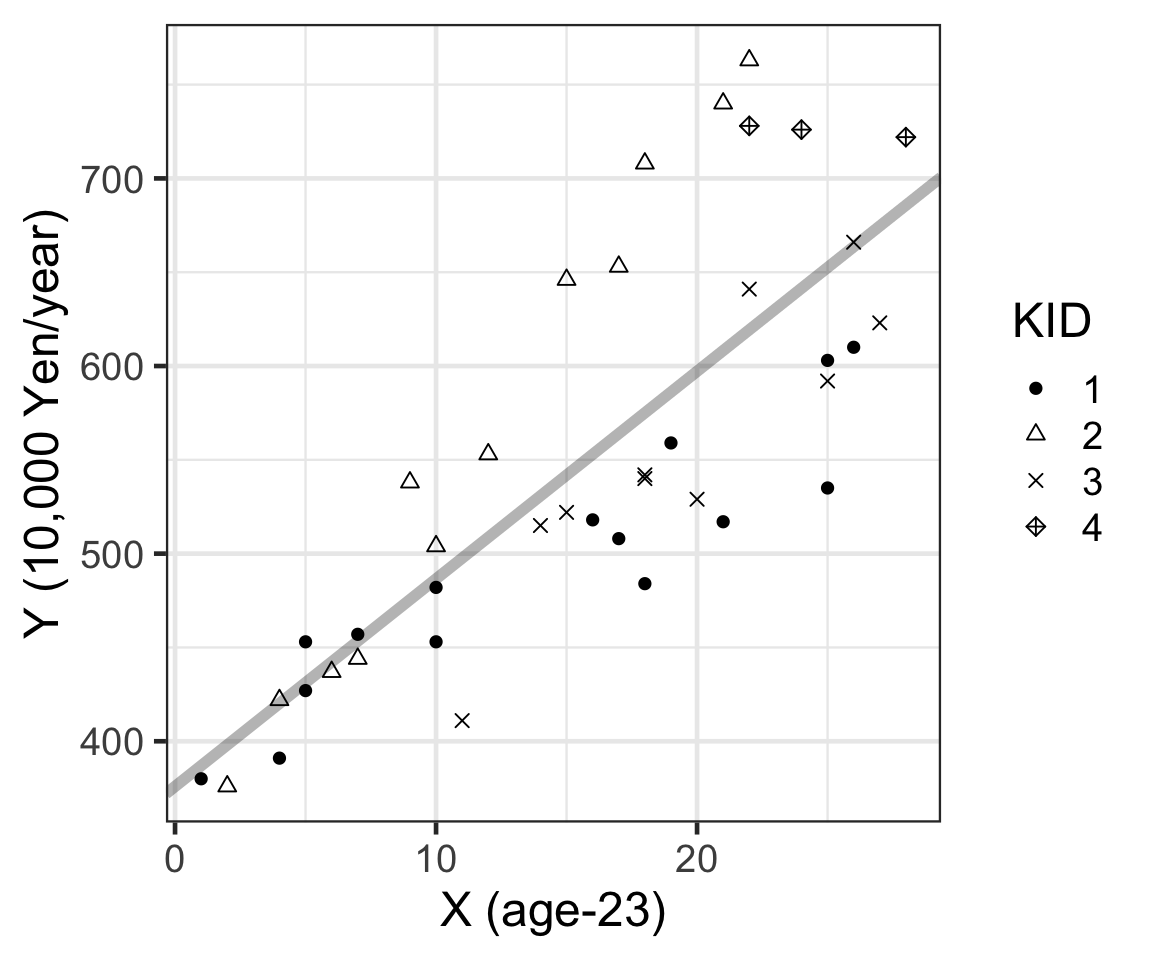
Figure 1: 年齡和年收入的散點圖,不同點的形狀代表不同的公司編號。
從總體的散點圖 1 來看,似乎年收入確實是隨着年齡增長而呈現直線增加的趨勢。但是公司編號 KID = 4 的三名社員薪水似乎是在同一水平的並無明顯變化。這一點可以把四家公司社員的數據分開來看更加清晰:
p <- ggplot(d, aes(X, Y, shape=KID))
p <- p + theme_bw(base_size=20)
p <- p + geom_abline(intercept=coef[1], slope=coef[2], size=2, alpha=0.3)
p <- p + facet_wrap(~KID)
p <- p + geom_line(stat='smooth', method='lm', se=FALSE, size=1, color='black', linetype='31', alpha=0.8)
p <- p + geom_point(size=3)
p <- p + scale_shape_manual(values=c(16, 2, 4, 9))
p <- p + labs(x='X (age-23)', y='Y (10,000 Yen/year)')
p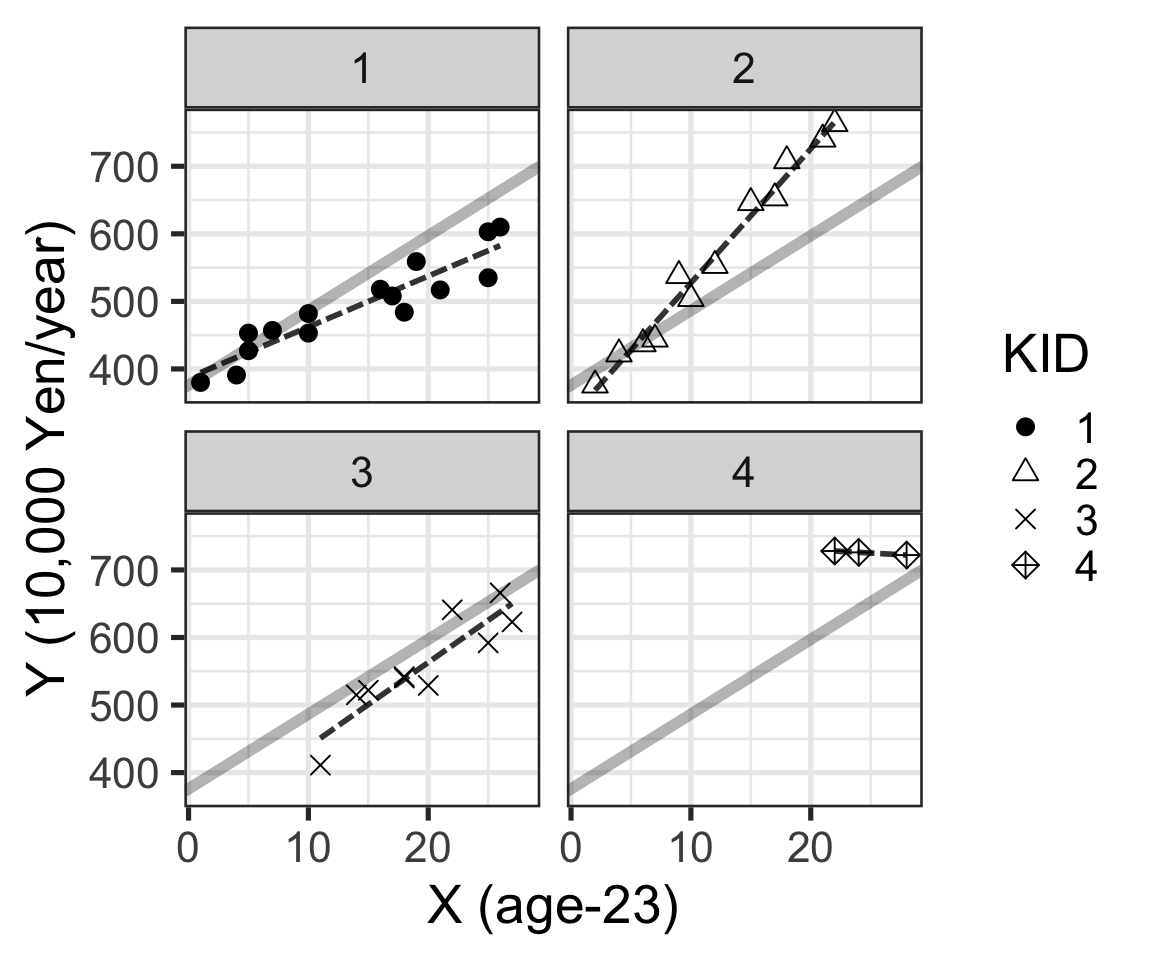
Figure 2: 年齡和年收入的散點圖,不同的公司在四個平面中展示,黑色點線是每家公司數據單獨使用線性回歸時獲得的直線。
如果不考慮組間(公司間)差異
- 模型的數學描述
\[ \begin{aligned} Y[n] & = y_{\text{base}}[n] + \varepsilon[n] & n = 1, \dots, N \\ y_{\text{base}}[n] & = a + bX[n] & n = 1, \dots, N \\ \varepsilon[n] & \sim \text{Normal}(0, \sigma_Y^2) & n = 1, \dots, N \\ \end{aligned} \]
當然,如果你想,模型可以直接簡化成:
\[ Y[n] \sim \text{Normal}(a + bX[n], \sigma^2_Y) \;\;\;\;\;\; n = 1, \dots, N \\ \]
上述簡化版的模型,翻譯成Stan語言如下:
data {
int N;
real X[N];
real Y[N];
}
parameters{
real a;
real b;
real<lower = 0> s_Y;
}
model {
for (n in 1 : N)
Y[n] = normal(a + b * X[n], s_Y);
}
下面的 R 代碼用來實現對上面 Stan 模型的擬合:
library(rstan)
d <- read.csv(file='../../static/files/data-salary-2.txt')
d$KID <- as.factor(d$KID)
data <- list(N=nrow(d), X=d$X, Y=d$Y)
fit <- stan(file='stanfiles/model8-1.stan', data=data, seed=1234)##
## SAMPLING FOR MODEL 'model8-1' NOW (CHAIN 1).
## Chain 1:
## Chain 1: Gradient evaluation took 1.3e-05 seconds
## Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.13 seconds.
## Chain 1: Adjust your expectations accordingly!
## Chain 1:
## Chain 1:
## Chain 1: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 1: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 1: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 1: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 1: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 1: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 1: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 1: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 1: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 1: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 1: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 1: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 1:
## Chain 1: Elapsed Time: 0.076557 seconds (Warm-up)
## Chain 1: 0.043822 seconds (Sampling)
## Chain 1: 0.120379 seconds (Total)
## Chain 1:
##
## SAMPLING FOR MODEL 'model8-1' NOW (CHAIN 2).
## Chain 2:
## Chain 2: Gradient evaluation took 5e-06 seconds
## Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.05 seconds.
## Chain 2: Adjust your expectations accordingly!
## Chain 2:
## Chain 2:
## Chain 2: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 2: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 2: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 2: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 2: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 2: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 2: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 2: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 2: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 2: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 2: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 2: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 2:
## Chain 2: Elapsed Time: 0.080947 seconds (Warm-up)
## Chain 2: 0.043589 seconds (Sampling)
## Chain 2: 0.124536 seconds (Total)
## Chain 2:
##
## SAMPLING FOR MODEL 'model8-1' NOW (CHAIN 3).
## Chain 3:
## Chain 3: Gradient evaluation took 3e-06 seconds
## Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.03 seconds.
## Chain 3: Adjust your expectations accordingly!
## Chain 3:
## Chain 3:
## Chain 3: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 3: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 3: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 3: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 3: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 3: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 3: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 3: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 3: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 3: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 3: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 3: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 3:
## Chain 3: Elapsed Time: 0.077026 seconds (Warm-up)
## Chain 3: 0.043674 seconds (Sampling)
## Chain 3: 0.1207 seconds (Total)
## Chain 3:
##
## SAMPLING FOR MODEL 'model8-1' NOW (CHAIN 4).
## Chain 4:
## Chain 4: Gradient evaluation took 5e-06 seconds
## Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.05 seconds.
## Chain 4: Adjust your expectations accordingly!
## Chain 4:
## Chain 4:
## Chain 4: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 4: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 4: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 4: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 4: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 4: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 4: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 4: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 4: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 4: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 4: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 4: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 4:
## Chain 4: Elapsed Time: 0.082446 seconds (Warm-up)
## Chain 4: 0.035819 seconds (Sampling)
## Chain 4: 0.118265 seconds (Total)
## Chain 4:fit## Inference for Stan model: model8-1.
## 4 chains, each with iter=2000; warmup=1000; thin=1;
## post-warmup draws per chain=1000, total post-warmup draws=4000.
##
## mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
## a 376.15 0.63 24.41 328.86 359.80 376.18 392.66 423.88 1483 1
## b 11.05 0.04 1.41 8.27 10.12 11.02 12.02 13.78 1527 1
## s_Y 68.42 0.21 8.26 54.41 62.59 67.64 73.53 86.73 1538 1
## lp__ -184.12 0.03 1.31 -187.60 -184.70 -183.76 -183.18 -182.66 1391 1
##
## Samples were drawn using NUTS(diag_e) at Mon May 18 16:58:23 2020.
## For each parameter, n_eff is a crude measure of effective sample size,
## and Rhat is the potential scale reduction factor on split chains (at
## convergence, Rhat=1).現在有更加方便的 rstanarm 包可以幫助我們省去寫 Stan 模型的過程:
library(rstanarm)
rstanarm_results = stan_glm(Y ~ X, data=d, iter=2000, warmup=1000, cores=4)
summary(rstanarm_results, probs=c(.025, .975), digits=3)##
## Model Info:
## function: stan_glm
## family: gaussian [identity]
## formula: Y ~ X
## algorithm: sampling
## sample: 4000 (posterior sample size)
## priors: see help('prior_summary')
## observations: 40
## predictors: 2
##
## Estimates:
## mean sd 2.5% 97.5%
## (Intercept) 376.371 24.615 328.532 423.842
## X 11.030 1.401 8.387 13.793
## sigma 68.159 8.136 54.474 86.401
##
## Fit Diagnostics:
## mean sd 2.5% 97.5%
## mean_PPD 548.026 15.100 517.682 577.179
##
## The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).
##
## MCMC diagnostics
## mcse Rhat n_eff
## (Intercept) 0.397 1.000 3836
## X 0.022 1.001 3940
## sigma 0.146 1.000 3112
## mean_PPD 0.245 1.000 3795
## log-posterior 0.029 1.001 1788
##
## For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).可以看到強制不同公司社員的年收入來自同一個正態分佈時,方差顯得非常的大。
如果要考慮組間差異
我們認爲每家公司社員新入職時的起點薪水不同(截距不同-隨機截距),進入公司之後隨年齡增加的薪水幅度也不同(斜率不同-隨機斜率)。因此,用 \(a[1]\sim a[K], K = 1, 2, 3, 4\) 表示每家公司的截距,用 \(b[1] \sim b[K], K = 1, 2, 3, 4\) 表示每家公司薪水上升的斜率。那麼每家公司的薪水年齡線性回歸模型可以寫作是 \(a[K] + b[K] X, K = 1, 2, 3, 4\)
- 模型數學描述
\[ Y[n] \sim \text{Normal}(a[\text{KID[n]}] + b[\text{KID}[n]] X[n], \sigma^2_Y) \\ n = 1, \dots, N \]
上述模型的 Stan 譯文如下:
data {
int N;
int K;
real X[N];
real Y[N];
int<lower = 1, upper = K> KID[N];
}
parameters {
real a[K];
real b[K];
real<lower = 0> s_Y;
}
model {
for (n in 1:N)
Y[n] ~ normal(a[KID[n]] + b[KID[n]] * X[n], s_Y);
}
下面的 R 代碼用來實現上面貝葉斯多組不同截距不同斜率線性回歸模型的擬合:
library(rstan)
d <- read.csv(file='../../static/files/data-salary-2.txt')
data <- list(N=nrow(d), X=d$X, Y=d$Y, KID = d$KID, K = 4)
fit <- stan(file='stanfiles/model8-2.stan', data=data, seed=1234)##
## SAMPLING FOR MODEL 'model8-2' NOW (CHAIN 1).
## Chain 1:
## Chain 1: Gradient evaluation took 1.7e-05 seconds
## Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.17 seconds.
## Chain 1: Adjust your expectations accordingly!
## Chain 1:
## Chain 1:
## Chain 1: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 1: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 1: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 1: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 1: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 1: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 1: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 1: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 1: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 1: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 1: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 1: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 1:
## Chain 1: Elapsed Time: 0.450551 seconds (Warm-up)
## Chain 1: 0.267262 seconds (Sampling)
## Chain 1: 0.717813 seconds (Total)
## Chain 1:
##
## SAMPLING FOR MODEL 'model8-2' NOW (CHAIN 2).
## Chain 2:
## Chain 2: Gradient evaluation took 5e-06 seconds
## Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.05 seconds.
## Chain 2: Adjust your expectations accordingly!
## Chain 2:
## Chain 2:
## Chain 2: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 2: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 2: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 2: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 2: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 2: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 2: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 2: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 2: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 2: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 2: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 2: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 2:
## Chain 2: Elapsed Time: 0.414798 seconds (Warm-up)
## Chain 2: 0.262094 seconds (Sampling)
## Chain 2: 0.676892 seconds (Total)
## Chain 2:
##
## SAMPLING FOR MODEL 'model8-2' NOW (CHAIN 3).
## Chain 3:
## Chain 3: Gradient evaluation took 5e-06 seconds
## Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.05 seconds.
## Chain 3: Adjust your expectations accordingly!
## Chain 3:
## Chain 3:
## Chain 3: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 3: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 3: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 3: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 3: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 3: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 3: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 3: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 3: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 3: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 3: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 3: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 3:
## Chain 3: Elapsed Time: 0.440107 seconds (Warm-up)
## Chain 3: 0.288008 seconds (Sampling)
## Chain 3: 0.728115 seconds (Total)
## Chain 3:
##
## SAMPLING FOR MODEL 'model8-2' NOW (CHAIN 4).
## Chain 4:
## Chain 4: Gradient evaluation took 5e-06 seconds
## Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.05 seconds.
## Chain 4: Adjust your expectations accordingly!
## Chain 4:
## Chain 4:
## Chain 4: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 4: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 4: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 4: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 4: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 4: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 4: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 4: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 4: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 4: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 4: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 4: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 4:
## Chain 4: Elapsed Time: 0.447923 seconds (Warm-up)
## Chain 4: 0.259137 seconds (Sampling)
## Chain 4: 0.70706 seconds (Total)
## Chain 4:fit## Inference for Stan model: model8-2.
## 4 chains, each with iter=2000; warmup=1000; thin=1;
## post-warmup draws per chain=1000, total post-warmup draws=4000.
##
## mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
## a[1] 387.16 0.28 14.18 359.00 377.67 387.06 396.34 415.21 2560 1
## a[2] 328.45 0.32 16.66 295.74 317.60 328.68 339.52 361.24 2649 1
## a[3] 314.06 0.66 34.62 246.26 290.04 314.33 337.91 381.39 2725 1
## a[4] 751.09 3.10 157.77 440.06 643.83 752.64 857.32 1063.97 2598 1
## b[1] 7.51 0.02 0.87 5.79 6.94 7.51 8.10 9.19 2381 1
## b[2] 19.88 0.02 1.23 17.51 19.07 19.88 20.70 22.32 2545 1
## b[3] 12.45 0.03 1.69 9.16 11.28 12.45 13.60 15.75 2661 1
## b[4] -1.04 0.12 6.36 -13.54 -5.34 -1.06 3.39 11.43 2616 1
## s_Y 27.32 0.07 3.57 21.48 24.77 26.95 29.43 35.38 2858 1
## lp__ -148.07 0.07 2.38 -153.72 -149.41 -147.68 -146.36 -144.57 1311 1
##
## Samples were drawn using NUTS(diag_e) at Mon May 18 16:59:02 2020.
## For each parameter, n_eff is a crude measure of effective sample size,
## and Rhat is the potential scale reduction factor on split chains (at
## convergence, Rhat=1).等級線性回歸的貝葉斯實現
模型機制 mechanism
如果我們認爲每家公司的起點薪水 \(a[k]\) 服從正態分佈,且該正態分佈的平均值是全體公司的起點薪水的均值 \(a_\mu\),方差是 \(\sigma^2_a\)。類似地,假設每家公司內隨着年齡增長而增加薪水的幅度 \(b[k]\) 也服從某個正態分佈,均值和方差分別是 \(b_\mu, \sigma^2_b\)。這樣我們就不僅僅是允許了各家公司的薪水年齡回歸直線擁有不同的斜率和截距,還對這些隨機斜率和截距的前概率分佈進行了設定。
此時,隨機效應模型的數學表達式就可以寫成下面這樣:
\[ \begin{aligned} Y[n] &\sim \text{Normal}(a[\text{KID[n]}] + b[\text{KID}[n]] X[n], \sigma^2_Y) & n = 1, \dots, N \\ a[k] &= a_\mu + a_\varepsilon[k] & k = 1, \dots, K \\ a_\varepsilon[k] & \sim \text{Normal}(0, \sigma^2_a) & k = 1, \dots, K \\ b[k] & = b_\mu + b_\varepsilon[k] & k = 1, \dots, K \\ b_\varepsilon[k] &\sim \text{Normal}(0, \sigma^2_b) & k = 1, \dots, K \end{aligned} \]
使用 rstanarm 包可以使用下面的代碼實現
library(rstanarm)
M1_stanlmer <- stan_lmer(formula = Y ~ X + (X | KID),
data = d,
seed = 1234)##
## SAMPLING FOR MODEL 'continuous' NOW (CHAIN 1).
## Chain 1:
## Chain 1: Gradient evaluation took 0.000116 seconds
## Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 1.16 seconds.
## Chain 1: Adjust your expectations accordingly!
## Chain 1:
## Chain 1:
## Chain 1: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 1: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 1: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 1: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 1: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 1: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 1: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 1: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 1: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 1: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 1: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 1: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 1:
## Chain 1: Elapsed Time: 7.72361 seconds (Warm-up)
## Chain 1: 3.71292 seconds (Sampling)
## Chain 1: 11.4365 seconds (Total)
## Chain 1:
##
## SAMPLING FOR MODEL 'continuous' NOW (CHAIN 2).
## Chain 2:
## Chain 2: Gradient evaluation took 2.5e-05 seconds
## Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.25 seconds.
## Chain 2: Adjust your expectations accordingly!
## Chain 2:
## Chain 2:
## Chain 2: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 2: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 2: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 2: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 2: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 2: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 2: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 2: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 2: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 2: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 2: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 2: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 2:
## Chain 2: Elapsed Time: 5.67096 seconds (Warm-up)
## Chain 2: 2.07953 seconds (Sampling)
## Chain 2: 7.75049 seconds (Total)
## Chain 2:
##
## SAMPLING FOR MODEL 'continuous' NOW (CHAIN 3).
## Chain 3:
## Chain 3: Gradient evaluation took 4.2e-05 seconds
## Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.42 seconds.
## Chain 3: Adjust your expectations accordingly!
## Chain 3:
## Chain 3:
## Chain 3: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 3: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 3: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 3: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 3: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 3: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 3: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 3: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 3: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 3: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 3: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 3: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 3:
## Chain 3: Elapsed Time: 7.81475 seconds (Warm-up)
## Chain 3: 3.88969 seconds (Sampling)
## Chain 3: 11.7044 seconds (Total)
## Chain 3:
##
## SAMPLING FOR MODEL 'continuous' NOW (CHAIN 4).
## Chain 4:
## Chain 4: Gradient evaluation took 3.7e-05 seconds
## Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.37 seconds.
## Chain 4: Adjust your expectations accordingly!
## Chain 4:
## Chain 4:
## Chain 4: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 4: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 4: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 4: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 4: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 4: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 4: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 4: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 4: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 4: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 4: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 4: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 4:
## Chain 4: Elapsed Time: 11.2964 seconds (Warm-up)
## Chain 4: 2.51584 seconds (Sampling)
## Chain 4: 13.8122 seconds (Total)
## Chain 4:print(M1_stanlmer, digits = 2)## stan_lmer
## family: gaussian [identity]
## formula: Y ~ X + (X | KID)
## observations: 40
## ------
## Median MAD_SD
## (Intercept) 358.76 15.31
## X 12.71 3.11
##
## Auxiliary parameter(s):
## Median MAD_SD
## sigma 29.93 3.79
##
## Error terms:
## Groups Name Std.Dev. Corr
## KID (Intercept) 24.36
## X 9.26 -0.15
## Residual 30.32
## Num. levels: KID 4
##
## ------
## * For help interpreting the printed output see ?print.stanreg
## * For info on the priors used see ?prior_summary.stanregsummary(M1_stanlmer,
pars = c("(Intercept)", "X","sigma",
"Sigma[KID:(Intercept),(Intercept)]",
"Sigma[KID:X,(Intercept)]", "Sigma[KID:X,X]"),
probs = c(0.025, 0.975),
digits = 2)##
## Model Info:
## function: stan_lmer
## family: gaussian [identity]
## formula: Y ~ X + (X | KID)
## algorithm: sampling
## sample: 4000 (posterior sample size)
## priors: see help('prior_summary')
## observations: 40
## groups: KID (4)
##
## Estimates:
## mean sd 2.5% 97.5%
## (Intercept) 357.39 18.40 312.29 390.14
## X 12.40 4.06 2.50 19.81
## sigma 30.32 3.91 23.68 38.98
## Sigma[KID:(Intercept),(Intercept)] 593.52 1322.20 1.72 3794.51
## Sigma[KID:X,(Intercept)] -34.16 170.47 -375.20 302.16
## Sigma[KID:X,X] 85.70 170.48 6.74 481.62
##
## MCMC diagnostics
## mcse Rhat n_eff
## (Intercept) 1.20 1.01 233
## X 0.25 1.02 267
## sigma 0.08 1.00 2545
## Sigma[KID:(Intercept),(Intercept)] 65.01 1.01 414
## Sigma[KID:X,(Intercept)] 8.90 1.01 367
## Sigma[KID:X,X] 10.07 1.01 287
##
## For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).和非貝葉斯版本的概率論隨機效應線性回歸模型的結果相對比一下:
library(lme4)
M1 <- lmer(formula = Y ~ X + (X | KID),
data = d,
REML = TRUE)
summary(M1)## Linear mixed model fit by REML ['lmerMod']
## Formula: Y ~ X + (X | KID)
## Data: d
##
## REML criterion at convergence: 387.2
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -2.3697 -0.5184 -0.0355 0.7635 1.8788
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## KID (Intercept) 504.00 22.450
## X 28.54 5.342 -1.00
## Residual 833.94 28.878
## Number of obs: 40, groups: KID, 4
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 358.207 15.385 23.283
## X 13.067 2.741 4.767
##
## Correlation of Fixed Effects:
## (Intr)
## X -0.848
## convergence code: 0
## boundary (singular) fit: see ?isSingular